深圳专版2018-2019学年七年级下学期数学期末模拟卷
试卷更新日期：2019-06-11 类型：期末考试
一、选择题
-
1. 下面4个汽车标志图案，其中不是轴对称图形的是（ ）
A、
B、
C、
D、
2. 已知空气的单位体积质量是0.01239g/cm3 ， 数据0.001239用科学记数法可表示为（ ）A、1.239×10﹣3 B、1.239×10﹣2 C、0.1239×10﹣2 D、12.39×10﹣43. 甲以每小时20km的速度行驶时，他所走的路程s（km）与时间t（h）之间可用公式s=20t来表示，则下列说法正确的是（ ）A、数20和s，t都是变量 B、s是常量，数20和t是变量 C、数20是常量，s和t是变量 D、t是常量，数20和s是变量4. 下列运算正确的是（ ）A、a2•a3=a6 B、（﹣a+b）（a+b）=b2﹣a2 C、（a3）4=a7 D、a3+a5=a85. 以下列各组长度的线段为边，能构成三角形的是（ ）A、8，4，4 B、5，6，12 C、6，8，10 D、1，2，36. 下列事件中，随机事件是（ ）A、在地球上，抛出去的篮球会下落 B、通常水加热到100℃时会沸腾 C、购买一张福利彩票中奖了 D、掷一枚骰子，向上一面的字数一定大于零7.如图，能判断直线AB∥CD的条件是（ ）
A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°8. 如图，E，B，F，C四点在一条直线上，且EB=CF，∠A=∠D，增加下列条件中的一个仍不能证明△ABC≌△DEF，这个条件是（ ）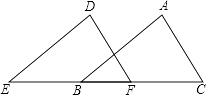
A、DF∥AC B、AB=DE C、∠E=∠ABC D、AB∥DE9. 如图，在∆ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E，若∠E=35 ，则∠BAC的度数为（ ）
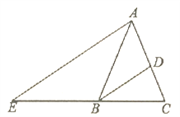A、 40
B、 45
C、 60
D、 70
10. 如图，△ABC中，AB=AC，AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，则下列五个结论：①AD上任意一点到AB，AC两边的距离相等；②AD上任意一点到B，C两点的距离相等；③AD⊥BC，且BD=CD；④∠BDE=∠CDF；⑤AE=AF．其中，正确的有（ ）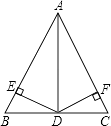
A、2个 B、3个 C、4个 D、5个二、填空题
-
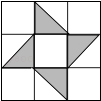
11. （﹣2018）0+（﹣1）﹣2= ．12. 一个角的补角是它的余角的4倍，则这个角等于度．13. 已知等腰三角形的一个内角为80°，则另两个角的度数是 ．14. 小球在如图所示的地板上自由地滚动，并随机地停留在某块方砖上，那么小球最终停留在黑色区域的概率是 ．
15. 小雨画了一个边长为3 cm的正方形，如果将正方形的边长增加x cm，那么面积的增加值y(cm2)与边长的增加值x(cm)之间的关系式为 ．16. 在全民健身环城越野赛中，甲、乙两选手的行程y（千米）随时间（时）变化的图象（全程）如图所示．有下列说法：①起跑后1小时内，甲在乙的前面；
②第1小时两人都跑了10千米；
③甲比乙先到达终点；
④两人都跑了20千米．
其中正确的说法的序号是 ．
三、解答题
-
17. 计算(1)、（12a3-6a2+3a）÷3a-1(2)、（2x+y+z)(2x-y-z)18. 先化简，再求值：（﹣x﹣2y）（x﹣2y）+（2x3﹣4x2y）÷2x，其中x＝﹣2，y＝1．19. 如图，在△ABC中，∠B=50°，AD平分∠CAB，交BC于D，E为AC边上一点，连接DE，∠EAD=∠EDA，EF⊥BC于点F．求∠FED的度数．
20. 一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球．若红球个数是黑球个数的2倍多40个．从袋中任取一个球是白球的概率是 ．(1)、求袋中红球的个数；(2)、求从袋中任取一个球是黑球的概率．21. 如图，已知BC∥GE，AF∥DE，点D在直线BC上，点F在直线GE上，且∠1=50°．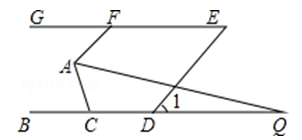
(1)、求∠AFG的度数；(2)、若AQ平分∠FAC，交直线BC于点Q，且∠Q=18°，则∠ACB的度数为°.（直接写出答案）22. 小红星期天从家里出发骑车去舅舅家做客，当她骑了一段路时，想起要买个礼物送给表弟，于是又折回到刚经过的一家商店，买好礼物后又继续骑车去舅舅家，以下是她本次去舅舅家所用的时间与路程的关系式示意图．根据图中提供的信息回答下列问题：
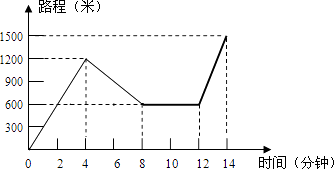(1)、小红家到学校的路程是米，小红在商店停留了分钟；(2)、在整个去舅舅家的途中哪个时间段小红骑车速度最快，最快的速度是多少米/分？(3)、本次去舅舅家的行程中，小红一共行驶了多少米？一共用了多少分钟？23. 在 中， ， ，点 是 的中点，点 是 上的一点（点 不与点 ， 重合）.过点 ，点 作直线 的垂线，垂足分别为点 和点 .
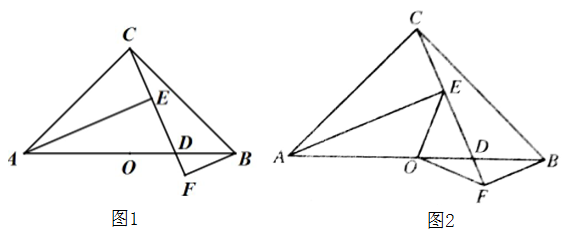(1)、如图1，求证： ；(2)、如图2，连接 ， ，请判断线段 与 之间的数量关系和位置关系，并说明理由.