江苏省苏州市高新区2018-2019学年九年级下学期数学中考二模试卷
试卷更新日期:2019-06-10 类型:中考模拟
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 计算3-1的结果是( )A、3 B、 C、 D、2. 每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其忧。据测定,杨絮纤维的直径约为 ,该数值用科学记数法表示为( )A、 B、 C、 D、3. 下列美丽的图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,点E在AD延长线上,下列条件中不能判定BC∥AD的是( )
4. 如图,点E在AD延长线上,下列条件中不能判定BC∥AD的是( ) A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、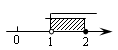 D、
D、 6. 如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是( )
6. 如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是( ) A、 B、 C、 D、7. 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( ).
A、 B、 C、 D、7. 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( ). A、45° B、85° C、90° D、95°8. 如图, 的顶点 与坐标原点重合, =90°, ,当点 在反比例函数 ( >0)的图像上移动时,点 的坐标满足的函数解析式为 ( )
A、45° B、85° C、90° D、95°8. 如图, 的顶点 与坐标原点重合, =90°, ,当点 在反比例函数 ( >0)的图像上移动时,点 的坐标满足的函数解析式为 ( ) A、 B、 C、 D、9. 如图,以O为圆心的圆与直线y=-x+ 交于A、B两点,若△OAB恰为等边三角形,则弧AB的长度为( )
A、 B、 C、 D、9. 如图,以O为圆心的圆与直线y=-x+ 交于A、B两点,若△OAB恰为等边三角形,则弧AB的长度为( ) A、 π B、π C、 π D、10. 如图,矩形ABCD中,AB=3,AD= ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
A、 π B、π C、 π D、10. 如图,矩形ABCD中,AB=3,AD= ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( ) A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题(本大题共8小题,每小题3分,共24分)
-
11. 在函数 中,自变量 的取值范围是 .12. 分解因式: .13. 一个圆锥的底面半径为3 ,将其侧面展开,得到的扇形圆心角为 ,则此圆锥的母线长为 .14. 关于x的方程 的一个根为3,则该方程的另一个根是 .15. 如图,△ABC是一块直角三角板,∠BAC=90°,∠B=30°,现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED的度数为°.
 16. 如图,在楼顶点 处观察旗杆 测得旗杆顶部 的仰角为30°,旗杆底部 的俯角为45°.已知楼高 m,则旗杆 的高度为 . (结果保留根号)
16. 如图,在楼顶点 处观察旗杆 测得旗杆顶部 的仰角为30°,旗杆底部 的俯角为45°.已知楼高 m,则旗杆 的高度为 . (结果保留根号)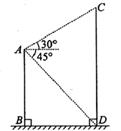 17. 某班的中考英语听力口语模拟考试成绩如下:
17. 某班的中考英语听力口语模拟考试成绩如下:考试成绩/分
30
29
28
27
26
学生数/人
20
15
10
2
2
该班中考英语听力口语模拟考试成绩的众数比中位数多分.
18. 如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则 的值为 .
三、解答题(本大题共10小题,共76分。)
-
19. 计算: .20. 解不等式组:21. 先化简,再求值: ,其中 是满足 的整数.22. 为响应建设“美丽乡村”,大桥村在河岸上种植了柳树和香樟树,已知种植柳树的棵数比香樟树的棵数多22棵,种植香樟树的棵树比总数的三分之一少2棵.问这两种树各种了多少棵?23. 小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位: )并绘制了样本的频数分布表和频数分布直方图(如图) .

月均用水量(单位: )
频数
百分比
2
4%
12
24%
10
20%
12%
3
6%
2
4%
(1)、请根据题中己有的信息补全频数分布表和频数分布直方图;(2)、如果家庭月均用水量“大于或等于4 且小于7 ”为中等用水量家庭,请你估计小王所居住的小区中等用水量家庭大约有多少户?(3)、从月均用水量在 , 这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.24. 如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E. (1)、求证:BE=CD;(2)、连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.25. 如图,在平面直角坐标系中,点 在 轴正半轴上, 轴,点 、 的横坐标都是3,且 ,点 在 上,若反比例函数 的图象经过点 、 ,且 .
(1)、求证:BE=CD;(2)、连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.25. 如图,在平面直角坐标系中,点 在 轴正半轴上, 轴,点 、 的横坐标都是3,且 ,点 在 上,若反比例函数 的图象经过点 、 ,且 . (1)、求 的值及点 的坐标;(2)、将 沿着 折叠,设顶点 的对称点 的坐标是 ,求代数式 的值.26. 如图,直线x=-4与x轴交于E,一开口向上的抛物线过原点O交线段OE于A,交直线x=-4于B.过B且平行于x轴的直线与抛物线交于C,直线OC交直线AB于D,且AD:BD=1:3.
(1)、求 的值及点 的坐标;(2)、将 沿着 折叠,设顶点 的对称点 的坐标是 ,求代数式 的值.26. 如图,直线x=-4与x轴交于E,一开口向上的抛物线过原点O交线段OE于A,交直线x=-4于B.过B且平行于x轴的直线与抛物线交于C,直线OC交直线AB于D,且AD:BD=1:3. (1)、求点A的坐标;(2)、若△OBC是等腰三角形,求此抛物线的函数关系式.27. 如图,△ABC内接于⊙O,AC是直径,点D是AC延长线上一点, 且∠DBC=∠BAC, .
(1)、求点A的坐标;(2)、若△OBC是等腰三角形,求此抛物线的函数关系式.27. 如图,△ABC内接于⊙O,AC是直径,点D是AC延长线上一点, 且∠DBC=∠BAC, . (1)、求证:BD是⊙O的切线;(2)、求 的值;(3)、如图,直径AC=5, ,求△ABF面积.28. 如图1,已知点A(2,0),B(0,4),∠AOB的平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P、Q关于直线OC的对称点M、N.设P运动的时间为t(0<t<2)秒.
(1)、求证:BD是⊙O的切线;(2)、求 的值;(3)、如图,直径AC=5, ,求△ABF面积.28. 如图1,已知点A(2,0),B(0,4),∠AOB的平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P、Q关于直线OC的对称点M、N.设P运动的时间为t(0<t<2)秒. (1)、求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);(2)、设△MNC与△OAB重叠部分的面积为S.
(1)、求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);(2)、设△MNC与△OAB重叠部分的面积为S.①试求S关于t的函数关系式;
②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.