江苏省常熟市九校2019届九年级数学中考二模试卷

试卷更新日期：2019-06-10 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题；每小题3分，共30分。）

1. 2的相反数是（）

A、 $\frac{1}{2}$ B、2 C、﹣2 D、 $- \frac{1}{2}$

查看试题解析
2. 下列四个图案中，是轴对称图案的是 $($ $)$

A、 B、 C、 D、

查看试题解析
3. 下列运算中，正确的是（）

A、 $3 a + 2 a^{2} = 5 a^{3}$ B、 $a \cdot a^{4} = a^{4}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(- 3 x^{3})}^{2} = 9 x^{6}$

查看试题解析
4. 如果方程x²-x+m＝0有两个不相等的实数根，则m的取值范围是（）

A、m＞ $\frac{1}{4}$ B、m≥ $\frac{1}{4}$ C、m＜ $\frac{1}{4}$ D、m≤ $\frac{1}{4}$

查看试题解析
5. 在2019年的体育中考中，某校6名学生的体育成绩统计如图，则这组数据的众数、中位数、平均数依次是（）

A、48，48，48 B、48，47.5，47.5 C、48，48，48.5 D、48，47.5，48.5

查看试题解析
6. 关于反比例函数y＝ $\frac{2}{x}$ 的图像，下列说法正确的是（）

A、图像经过点（1，1） B、两个分支分布在第二、四象限 C、当x＜0时，y随x的增大而减小 D、两个分支关于x轴成轴对称

查看试题解析
7. 如图，“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形，随机在大正方形及其内部区域投针．若针扎到小正方形（阴影部分）的概率是 $\frac{1}{4}$ ，则大、小两个正方形的边长之比是（）

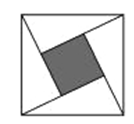A、4：1 B、2：1 C、 $\sqrt{2}$ ：1 D、1：2

查看试题解析
8. 如图，在下列网格中，小正方形的边长均为1，点A、B、O都在格点上，则∠AOB的正弦值是（）

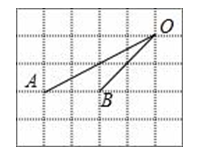A、 $\frac{3 \sqrt{10}}{10}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{\sqrt{10}}{10}$

查看试题解析
9. 如图，在平面直角坐标系xOy中，已知△ABC，∠ABC=90°，顶点A在第一象限，B，C在x轴的正半轴上（C在B的右侧），BC=2，AB= $2 \sqrt{3}$ ，△ADC与△ABC关于AC所在的直线对称．若点A和点D在同一个反比例函数 $y = \frac{k}{x}$ 的图像上，则OB的长是 $($ $)$

A、2 B、3 C、 $2 \sqrt{3}$ D、 $3 \sqrt{3}$

查看试题解析
10. 如图，以任意 $Δ A B C$ 的边 $A B$ 和 $A C$ 向形外作等腰Rt△ABD和等腰Rt△ACE， $F$ 、 $G$ 分别是线段 $B D$ 和 $C E$ 的中点，则 $\frac{C D}{F G}$ 的值等于 $($ $)$

A、 $\frac{2 \sqrt{3}}{3}$ B、 $\sqrt{2}$ C、 $\frac{3}{2}$ D、 $\sqrt{3}$

查看试题解析

二、填空题（本大题共8小题，每小题3分，共24分。）

11. 数据显示，今年高校毕业生规模达到7270000人，比去年有所增加．数据7270000人用科学记数法表示为人．

查看试题解析
12. 化简： $(m + 2 + \frac{5}{2 - m}) \cdot \frac{2 m - 4}{3 - m}$ ＝．

查看试题解析
13. 直线l₁∥l₂ ，一块含45°角的直角三角板如图放置，∠1＝85°，则∠2＝．

查看试题解析
14. 若 $a + b = 4$ ， $a - b = 1$ ，则 ${(a + 2)}^{2} - {(b - 2)}^{2}$ 的值为．

查看试题解析
15. 小红用一张半径为6cm，圆心角为 $120 °$ 的扇形纸片做成一个圆锥形的小帽子，则这个圆锥形小帽子的高为cm．

查看试题解析
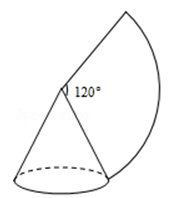16. 如图在平面直角坐标系中，周长为12的正六边形ABCDEF的对称中心与原点O重合，点A在x轴上．点B，在反比例函数y $= \frac{k}{x}$ 位于第一象限的图像上．则
k的值为．

查看试题解析
17. 已知 $x$ 轴上一点 $A (1$ ， $0)$ ， $B$ 为 $y$ 轴上的一动点，连接 $A B$ ，以 $A B$ 为边作等边 $Δ A B C$ 如图所示，已知点 $C$ 随着点 $B$ 的运动形成的图形是一条直线，连接 $O C$ ，则 $A C + O C$ 的最小值是．

查看试题解析

三、解答题（本大题共11小题，共76分。）

18. |-1|- $\frac{1}{2} \sqrt{8}$ -(5-π)⁰+4cos45°

查看试题解析
19. 解不等式组： ${\begin{matrix} x - 3 (x - 2) \leq 8 \\ x - 1 < \frac{x + 1}{3} \end{matrix}$ ．

查看试题解析
20. 五一期间，甲、乙两人在附近的景点游玩，甲从A、B两个景点中任意选择一个游玩，乙从A、B、C三个景点中任意选择一个游玩．

(1)、乙恰好游玩A景点的概率为；

(2)、用列表或画树状图的方法列出所有等可能的结果．并求甲、乙恰好游玩同一景点的概率．

查看试题解析
21. 如图，▱ABCD的对角线AC、BD相交于点O，AE＝CF．

(1)、求证：△BOE≌△DOF；

(2)、若BD＝EF，连接DE、BF，判断四边形EBFD的形状，并证明你的结论．

查看试题解析
22. 某企业工会开展“一周工作量完成情况”调查活动，随机调查了部分员工一周的工作量剩余情况，并将调查结果统计后绘制成如图1和图2所示的不完整统计图．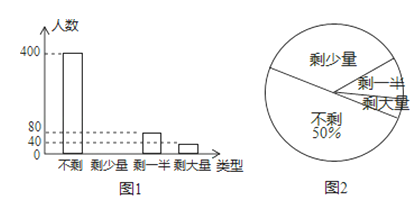

(1)、被调查员工人数为人，并把条形统计图补充完整；

(2)、求扇形统计图中“剩一半”项目所对应扇形的圆心角度数；

(3)、若该企业有员工10000人，请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人？

查看试题解析
23. 某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如表：

x/元

…

15

20

25

…

y/件

…

25

20

15

…

已知日销售量y是销售价x的一次函数．

(1)、求日销售量y（件）与每件产品的销售价x（元）之间的函数表达式；

(2)、当每件产品的销售价定为35元时，此时每日的销售利润是多少元？

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，抛物线 $y = - \frac{1}{6} x^{2} + b x + c$ 过点 $A (0 ， 4)$ 和 $C (8 ， 0)$ ， $P (t ， 0)$ 是 $x$ 轴正半轴上的一个动点， $M$ 是线段 $A P$ 的中点，将线段 $M P$ 绕点 $P$ 顺时针旋转 $90 °$ 得线段 $P B$ ，过点 $B$ 作 $x$ 轴的垂线，过点 A 作 $y$ 轴的垂线，两直线交于点 $D$ ．

(1)、求 $b$ 、 $c$ 的值；

(2)、当 $t$ 为何值时，点 $D$ 落在抛物线上．

查看试题解析
25. 已知：BD为⊙O的直径，点A为圆上一点，直线BF交DA的延长线于点F，点C为⊙O上一点，AB＝AC，连接BC交AD于点E，连接AC，且∠ABF＝∠ABC．

(1)、如图1，求证：BF作⊙O的切线；

(2)、如图2，点H为⊙O内部一点，连接OH，CH．如果∠OHC＝∠HCA＝90°，猜想CH与DA的数量关系，并加以证明．

(3)、在（2）的条件下，若OH＝6，⊙O的半径为10．记△AEC面积为 $S_{1}$ ，△ABE面积为 $S_{2}$ ．求 $\frac{S_{1}}{S_{2}}$ 的值．

查看试题解析
26. 如图（1），在平面直角坐标系中，点A、C分别在y轴和x轴上，AB∥x轴，cosB= $\frac{3}{5}$ ．点P从B点出发，以1cm/s的速度沿边BA匀速运动，点Q从点A出发，沿线段AO−OC−CB匀速运动．点P与点Q同时出发，其中一点到达终点，另一点也随之停止运动．设点P运动的时间为t（s），△BPQ的面积为S（cm²），已知S与t之间的函数关系如图（2）中的曲线段OE、线段EF与曲线段FG．

(1)、点Q的运动速度为cm/s，点B的坐标为；

(2)、求曲线FG段的函数解析式；

(3)、当t为何值时，△BPQ的面积是四边形OABC的面积的 $\frac{1}{10}$ ？

查看试题解析
27. 如图，抛物线 $y = a x^{2} + 6 x + c$ 交x轴于A、B，两点，交y轴于点C．直线 $y = x - 5$ 经过点B、C．

(1)、求抛物线的解析式；

(2)、过点 $\frac{1}{10}$ 的直线交直线 $B C$ 于点 $M$ ．
①当 $A M ⊥ B C$ 时，过抛物线上一动点 $P$ （不与点 $B$ ， $C$ 重合），作直线 $A M$ 的平行线交直线 $B C$ 于点 $Q$ ，若以点 $\frac{1}{10}$ ， $M$ ， $P$ ， $Q$ 为顶点的四边形是平行四边形，求点 $P$ 的横坐标；

②连接 $A C$ ，当直线 $A M$ 与直线 $B C$ 的夹角等于 $∠ A C B$ 的2倍时，请直接写出点 $M$ 的坐标．

查看试题解析

x/元	…	15	20	25	…
y/件	…	25	20	15	…