江苏省苏州市昆山2018–2019学年九年级下学期数学中考二模试卷

试卷更新日期：2019-06-10 类型：中考模拟

进入出卷网下载

一、选择题(本大题共10小题，每小题3分，共30分)

1. －3的相反数是（）

A、 $\frac{1}{3}$ B、3 C、0 D、 $- \frac{1}{3}$

查看试题解析
2. 据报道，人类首张黑洞照片于北京时间2019年4月10日在全球六地同步发布，该黑洞位于室女座一个巨椭圆星系M87的中心，距离地球5500万光年。其中5500万用科学记数法表示为（）

A、55 x 10⁶ B、5. 5 x 10⁶ C、0. 55 x 10⁸ D、5. 5 x 10⁷

查看试题解析
3. 一组数据:2,4,6,4,8的中位数和众数分别是（）

A、6, 4 B、4, 4 C、6, 8 D、4, 6

查看试题解析
4. 下列运算中，正确的是（）

A、 $a + a = 2 a^{2}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、（-2a）²=4a² D、 ${(a - 1)}^{2} = a^{2} + 1$

查看试题解析
5. 若 $x < y$ ，则下列结论正确的是（）

A、 $- \frac{1}{3} x > - \frac{1}{3} y$ B、 $2 x > 2 y$ C、 $x - 1 > y - 1$ D、 $x^{2} < y^{2}$

查看试题解析
6. 如图，直线 $a ， b$ 被直线 $c$ 所截， $a / / b ， ∠ 2 = ∠ 3$ ，若 $∠ 1 = 130 °$ ，则 $∠ 4$ 等于（）

A、50° B、60° C、65° D、75°

查看试题解析
7. 用“描点法”画二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像时.列了如下表格：

根据表格上的信息回答问题：一元二次方程 $a x^{2} + b x + c - 5 = 0$ 的解为（）

A、 $x_{1} = - 2 ， x_{2} = 4$ B、 $x_{1} = - 1 ， x_{2} = 3$ C、 $x_{1} = 3 ， x_{2} = 4$ D、 $x_{1} = - 4 ， x_{2} = 4$

查看试题解析
8. 如图，⊙ $O$ 中，直径 $A B$ 与弦 $C D$ 相交于点 $E$ ，连接 $B C ， A D$ ，过点 $C$ 的切线与 $A B$ 的延长线交于点 $F$ ，若 $∠ D = 65 °$ ，则 $∠ F$ 的度数等于（）

A、30° B、35° C、40° D、45°

查看试题解析
9. 如图，平面直角坐标系中，菱形 $A B C D$ 的顶点 $A (3 ， 0) ， B (- 2 ， 0)$ ，顶点 $D$ 在 $y$ 轴正半轴上，则点 $C$ 的坐标为（）

A、(－3， 4 ) B、(－4， 5) C、(－5， 5) D、(－5， 4 )

查看试题解析
10. 如图，正方形 $A B C D$ 的边长为6，点 $E ， F$ 分别在边 $A B ， B C$ 上，若 $F$ 是 $B C$ 的中点，且 $∠ E D F = 45 °$ ，则 $D E$ 的长为（）

A、 $\frac{5}{3} \sqrt{10}$ B、 $2 \sqrt{10}$ C、 $3 \sqrt{5}$ D、 $\frac{10}{3} \sqrt{5}$

查看试题解析

二、填空题(本大题共8题，每小题3分，共24分，)

11. (－2)²平方根等于.

查看试题解析
12. 分解因式： $a^{3} - a b^{2}$ =.

查看试题解析
13. 函数y= $\frac{\sqrt{1 - 2 x}}{x}$ 的自变量x的取值范围是．

查看试题解析
14. 如图，一个正六边形转盘被分成6个全等三角形，任意转动这个转盘1次，当转盘停止转动时，指针指向阴影区域的概率是.

查看试题解析
15. 如图，把 $Δ A B C$ 绕点 $A$ 顺时针方旋转36°得到 $Δ A B^{'} C^{'}$ ，若 $B^{'} C^{'}$ 正好经过 $B$ 点，则 $∠ A B C$ =°

查看试题解析
16. 如图，在4 x5的正方形网格中，点 $A ， B ， C$ 都在格点上，则 $\tan ∠ A B C$ =.

查看试题解析
17. 如图，直线 $y = \frac{1}{2} x$ 与双曲线 $y = \frac{k}{x} (x > 0)$ 交于点 $A$ ，将直线 $y = \frac{1}{2} x$ 向上平移4个单位长度后，与双曲线 $y = \frac{k}{x} (x > 0)$ 交于点 $B$ ，与 $y$ 轴交于点 $C$ ，若 $O A = 3 B C$ ，则 $k$ 的值为.

查看试题解析
18. 已知关于 $x$ 的方程 $x^{2} - 4 x + t - 2 = 0$ ( $t$ 为实数)两非负实数根 $a, b$ ，则 $(a^{2} - 1) (b^{2} - 1)$ 的最小值是.

查看试题解析

三、解答题(本大题共10小题，共76分)

19. 计算： ${(- \sqrt{2})}^{2} - | - 3 + 5 | + {(1 - \sqrt{3})}^{0}$ .

查看试题解析
20. 解不等式组 ${\begin{cases} 4 x - 7 < 5 (x - 1) \\ \frac{x - 1}{3} \geq \frac{1}{2} x - 1 \end{cases}$ ，并写出该不等式组的整数解.

查看试题解析
21. 先化简再求值: $\frac{a^{2} - a}{a^{2} - 2 a + 1} \div (a + 1 - \frac{2 a - 1}{a - 1})$ ，并从 $0, 1, \sqrt{3}, 2$ 四个数中，给 $a$ 选取一个恰当的数进行求值.

查看试题解析
22. 某校计划购买一批篮球和足球，已知购买2个篮球和1个足球共需320元，购买3个篮球和2个足球共需540元.

(1)、求每个篮球和每个足球的售价;

(2)、如果学校计划购买这两种球共50个，用于此次购球的总资金不低于5400元，且不超过5500元，求本次购球方案.

查看试题解析
23. 如图，等腰 $R t Δ A B C$ 中， $A C = B C ， ∠ A C B = 90 °$ ，点 $D$ 为斜边 $A B$ 上一点 (不与 $A ， B$ 重合)，连接 $C D$ ，将线段 $C D$ 绕点 $C$ 顺时针方向旋转90°至 $C E$ ，连接 $A E$ .

(1)、求证： $Δ A E C ≅ Δ B D C$ ；

(2)、若 $A D ： B D = \sqrt{3} ： 1$ ，求 $∠ A E C$ 的度数.

查看试题解析
24. 如图所示，两个可以自由转动的转盘中，指针位置固定，每个转盘被分成面积相等的三个扇形，其中A转盘分别标有数字1，2，3，E转盘分别标有3，4，5.

(1)、转动A转盘一次，当转盘停止转动时，指针所指扇形中的数字是奇数的概率为.

(2)、转动A，B两个转盘各一次，当转盘停止转动时，求两指针所指扇形中的数字之积为偶数的概率.(用画树状图或列表等方法求解)

查看试题解析
25. 如图，在平面直角坐标系 $x O y$ 中，直线 $y = 2 x + b$ 经过点 $A (- 1 ， 0)$ ，与 $y$ 轴正半轴交于 $B$ 点，与反比例函数 $y = \frac{k}{x} (x > 0)$ 交于点 $C$ ，且 $B C = 2 A B ， B D / / x$ 轴交反比例函数 $y = \frac{k}{x} (x > 0)$ 于点 $D$ ，连接 $A D$ .

(1)、求 $b ， k$ 的值；

(2)、求 $Δ A B D$ 的面积；

(3)、若 $E$ 为线段 $B C$ 上一点，过点 $E$ 作 $E F / / B D$ ，交反比例函数 $y = \frac{k}{x} (x > 0)$ 于点 $F$ ，且 $E F = \frac{1}{2} B D$ .求点 $F$ 的坐标.

查看试题解析
26. 如图， $A B$ 是⊙ $O$ 的直径， $A C$ 是弦， $∠ B A C$ 的平分线 $A D$ 交⊙ $O$ 于点 $D ， D E ⊥ A C$ 交 $A C$ 的延长线于点 $E$ ，连接 $B D ， O E ， O E$ 交 $A D$ 于点 $F$ .

(1)、求证： $D E$ 是⊙ $O$ 的切线；

(2)、若 $\frac{A C}{A B} = \frac{3}{5}$ ，求 $\frac{A F}{D F}$ 的值；

(3)、在(2)的条件下，若⊙ $O$ 直径为10，求 $B D$ 的长.

查看试题解析
27. 如图，在 $R t Δ A B C$ 中， $∠ C = 90 ° ， A C = 5 ， ∠ B = 30 °$ ，点 $D$ 从点 $B$ 出发沿 $B A$ 方向以每秒2个单位长度的速度向点 $A$ 匀速运动，同时点 $E$ 从点 $A$ 出发沿 $A C$ 方向以每秒1个单位长度的速度向点 $C$ 匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点 $D ， E$ 运动的时间是： $t$ ( $t$ >0).过点 $D$ 作 $D F ⊥ B C$ 于点 $F$ ，连接 $D E ， E F$ .

(1)、则 $D F$ =(用含 $t$ 的代数式表示)；

(2)、在运动过程中(点 $E$ 不与点 $C$ 重合)，若过 $C ， E ， F$ 三点的⊙ $O$ 与 $A B$ 边相切时，求 $t$ 的值；

(3)、当 $t$ 为何值时， $Δ D E F$ 为直角三角形?请说明理由.

查看试题解析
28. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 交 $x$ 轴于点 $A (2 ， 0) ， B (- 3 ， 0)$ ，交 $y$ 轴于点 $C$ ，且经过点 $D (- 6 ， - 6)$ ，连接 $A D ， B D$ .

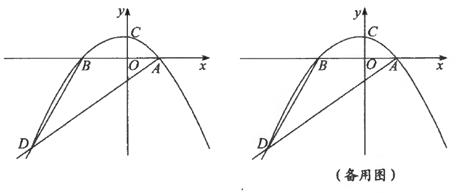(1)、求该抛物线的函数关系式；

(2)、若点 $M$ 为 $x$ 轴上方的抛物线上一点，能否在点 $A$ 左侧的 $x$ 轴上找到另一点 $N$ ，使得 $Δ A M N$ 与 $Δ A B D$ 相似?若相似，请求出此时点 $M$ 、点 $N$ 的坐标；若不存在，请说明理由；

(3)、若点 $P$ 是直线 $A D$ 上方的抛物线上一动点(不与点 $A ， D$ 重合)，过 $P$ 作 $P Q / / y$ 轴交直线 $A D$ 于点 $Q$ ，以 $P Q$ 为直径作⊙ $E$ ，则⊙ $E$ 在直线 $A D$ 上所截得的线段长度的最大值等于.(直接写出答案)

查看试题解析