浙江省嘉兴市秀洲区2018-2019学年九年级下学期初中毕业升学考试适应性练习数学试卷

试卷更新日期：2019-06-10 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分。）

1. 2^-2等于（）

A、 $\frac{1}{4}$ B、- $\frac{1}{4}$ C、4 D、-4

查看试题解析
2. 给出四个数：-1、0、 $\sqrt{5}$ 、 $\frac{2}{3}$ ，其中为无理数的是（）

A、-1 B、0 C、 $\sqrt{5}$ D、 $\frac{2}{3}$

查看试题解析
3. 下列各图中，不能折叠成一个立方体的是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、3a²+a²=4a⁴ B、(a²)³=a⁵ C、a·a²=a³ D、(2a)³=6a³

查看试题解析
5. 下列图形中，∠1一定小于∠2的是（）

A、 B、 C、 D、

查看试题解析
6. 某电动车厂2018年第三、四季度各月产量情况如图所示。某电动车厂2018年第三、四季则下列说法错误的是（ )

A、7月份产量为300辆 B、从10月到11月的月产量增长最快 C、从11月到12月的月产量减少了20% D、第四季度比第三季度的产量增加了70%

查看试题解析
7. 如图，一辆超市购物车放置在水平地面上，其侧面四边形ABCD与地面某条水平线l在同一平面内，且AB∥l，若∠A=93°，∠D=111°，则直线CD与l所夹锐角的度数为（）

A、15° B、18° C、21° D、24°

查看试题解析
8. 数学课上，老师提出问题：“一次函数的图象经过点A（3，2)，B（-1，-6)，由此可求得哪些结论？”小明思考后求得下列4个结论：①该函数表达式为y=2x-4；②该一次函数的函数值随自变量的增大而增大；③点P（2a，4a-4)在该函数图象上；④直线AB与坐标轴围成的三角形的面积为8．其中错误的结论是（）

A、① B、② C、③ D、④

查看试题解析
9. 如图，在扇形OAB中，点C是弧AB上任意一点（不与点A，B重合），CD∥OA交OB于点D，点I是△OCD的内心，连结OI，BI．若∠AOB=β，则∠OIB等于( ）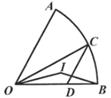

A、180°- $\frac{1}{2}$ β B、180°-β C、90°+ $\frac{1}{2}$ β D、90°+β

查看试题解析
10. 如图，在直角坐标系中，O为坐标原点，点A（4，0），以OA为对角线作正方形ABOC，若将抛物线y= $\frac{1}{2}$ x²沿射线OC平移得到新抛物线y= $\frac{1}{2}$ （x-m）²+k（m＞0）．则当新抛物线与正方形的边AB有公共点时，m的值一定是（）

A、2，6，8 B、0<m≤6 C、0<m≤8 D、0<m≤2 或 6 ≤ m≤8

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 已知∠α=60°，则∠α的余角等于．

查看试题解析
12. 抛掷一枚硬币，反面朝上的概率是。

查看试题解析
13. 因式分解：a³-4a²+42=。

查看试题解析
14. 方程 $\frac{2}{1 - x^{2}} = \frac{1}{x - 1}$ 的解为。

查看试题解析
15. 如图，点C为半圆的中点，AB是直径，点D是半圆上一点，AC，BD交于点E．若AD=1，BD=7，则CE的长为。

查看试题解析
16. 如图，在直角坐标系中，O为坐标原点，点A（1，2)，过点A分别作x轴、y轴的平行线交反比例函数y= $\frac{k}{x}$ （x>0)的图象于点B，C，延长OA交BC于点D．若△ABD的面积为2，则k的值为。

查看试题解析

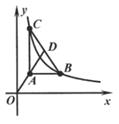
三、解答题（本题有8小题，第17~19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）

17.

(1)、计算：sin30°+|-3|- $\sqrt{4}$ ．

(2)、化简： $\frac{a b}{a + b} \cdot (\frac{a}{b} - \frac{b}{a})$

查看试题解析

18. 小红同学想仅用一架天平和一个10克的砝码测量出壹元硬币和伍角硬币的质量。于是，他找来足够多的壹元和伍角硬币（假设同种类每枚硬币的质量相同），经过操作得到如下记录．

记录	天平左边	天平右边	状态
记录一	5枚壹元硬币 1个10克的砝码	10枚伍角硬币	平衡
记录二	15枚壹元硬币	20枚伍角硬币 1个10克的砝码	平衡

请你帮小红同学算一算，一枚壹元硬币和一枚伍角硬币的质量分别是多少克?

查看试题解析

19. 如图是6×6的正方形网格，点A，B，C均在格点上．请按下列要求完成作图：①仅用无刻度直尺，且不能用直尺中的直角；②保留作图痕迹．

(1)、在图中作出一个以点A，B，C，D为顶点的平行四边形．

(2)、在图中作出△ABC中AB边上的中线．

查看试题解析
20. 若一个正整数能表示为两个连续自然数的平方差，则称这个正整数为“和谐数”。如：1=1²-0² ， 7=4²-3² ，因此1和7都是“和谐数”。

(1)、判断11是否为“和谐数”，并说明理由．

(2)、下面是某个同学演算后发现的两个命题，请选择其中一个命题，判断真假，并说明理由．
命题1：数2n-1(n为正整数)是“和谐数”。

命题2：“和谐数”一定是奇数。

查看试题解析
21. 某校九年级共有360名学生．为了解该校九年级学生每周运动的时间，从中随机抽取了若干名学生进行问卷调查，并将获得的数据（每周运动的时间，单位：小时)进行整理、描述和分析．下面给出了部分信息．
I．学生每周运动的时间的频数分布直方图如下（数据分成6组：1≤x<3，3≤x<5，5≤x<7，7≤x<9，9≤x<11，11≤x≤13)

Ⅱ．学生每周运动的时间在7≤x<9这一组的数据是：

7，7.2，7.4，7.5，7.5，7.6，7.8，7.8，8，8.2，8.4，8.5，8.6，8.8根据以上信息，解答下列问题：

(1)、求这次被抽取的学生数。

(2)、写出被抽取学生每周运动的时间的中位数．

(3)、根据此次问卷调查结果，估计该校九年级全体学生每周运动的时间超过7.9小时的学生有多少人?

查看试题解析
22. 图1是某酒店的推拉门，已知门的宽度AD=2米，两扇门的大小相同（即AB=CD)，且AB+CD=AD，现将右边的门CDD₁C₁绕门轴DD1向外面旋转67°（如图2所示）．

参考数据：(sin67°≈0.92，cos67°≈0.39，tan29.6°≈0.57，tan19.6°≈0.36，sin29.6°≈0.49）

(1)、求点C到直线AD的距离．

(2)、将左边的门ABB₁A₁绕门轴AA₁向外面旋转，设旋转角为a（如图3所示），问当a为多少度时，点B，C之间的距离最短．

查看试题解析
23. 已知，抛物线y=x²+2mx(m为常数且m≠0）．

(1)、判断该抛物线与x轴的交点个数，并说明理由．

(2)、若点A（-n+5，0），B(n-1，0)在该抛物线上，点M为抛物线的顶点，求△ABM的面积．

(3)、若点（2，p)，（3，g），（4，r)均在该抛物线上，且p<g<r，求m的取值范围．

查看试题解析
24. 数学拓展课上，老师给出如下定义：如果三角形有一边上的中线长恰好等于该边长的1.5倍，那么称这个三角形为“趣味三角形”．

理解：

(1)、如图1，在△ABC中，AB=AC= $\sqrt{10}$ ，BC=2，试判断△ABC是否为“趣味三角形”，并说明理由．

(2)、如图2，已知△ABC是“趣味三角形”，AD，BE，CF分别是BC，AC，AB边上的中线，且AD= $\frac{3}{2}$ BC，试探究BE和CF之间的位置关系。

(3)、如图3，直线l₁∥l₂ ， l₁与l₂之间的距离为2，点B，C在直线l₁上，点A在直线l₂上，AD，BE，CF分别是△ABC的边BC，AC，AB上的中线．若△ABC是“趣味三角形”，BC=2 $\sqrt{2}$ ．求BE²+CF²的值．

查看试题解析