浙江省宁波市慈溪市2018-2019学年九年级下学期数学中考模拟试卷(3月)
试卷更新日期:2019-06-10 类型:中考模拟
一、选择题(本题有12小题,每小题4分,共48分)
-
1. 2019的相反数( )A、 B、-2019 C、- D、20192. 下列计算正确的是( )A、3a-2a=1 B、-3a2÷(-a)=-a2 C、a2 . a3=a6 D、(a3)2=a63. 在“创新活力之城,美丽幸福慈溪”行动引领下,2018年慈溪GDP达到1737亿元,其中1737亿用科学技术法表示为( )A、1.737×1011元 B、1.737×1010元 C、1.737×1012元 D、1.737×109元4. 如图所示的几何体的左视图是( )
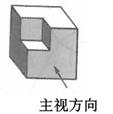 A、
A、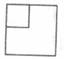 B、
B、 C、
C、 D、
D、 5. 不等式组 的解集是( )A、x>- B、x<- C、x<1 D、- <x<16. 下列电视台图标中,属于中心对称图形的是( )A、
5. 不等式组 的解集是( )A、x>- B、x<- C、x<1 D、- <x<16. 下列电视台图标中,属于中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,BE平分∠DBC,A是BD上一点,过点A作AE∥BC交BE于点E,∠DAE=56°,则∠E的度数为( )
7. 如图,BE平分∠DBC,A是BD上一点,过点A作AE∥BC交BE于点E,∠DAE=56°,则∠E的度数为( ) A、56° B、28° C、36° D、26°8. 在一次中国诗词大会中,百人团选手得分情况如表:
A、56° B、28° C、36° D、26°8. 在一次中国诗词大会中,百人团选手得分情况如表:人数
30
40
20
10
分数
80
85
90
95
那么这百人团选手所得分数的中位数和众数分别是( )
A、85和82.5 B、85.5和85 C、85和85 D、85.5和809. 已知圆锥的底面半径为6cm,圆锥的高为8cm,则这个圆锥的侧面积为( )A、60πcm2 B、48πcm2 C、30πcm2 D、24πcm210. 如图,八个完全相同的小长方形拼成一个正方形网格,连结小长方形的顶点所得的四个三角形中是相似三角形的是( )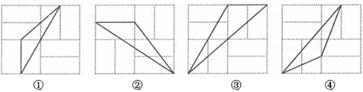 A、①和② B、②和③ C、①和③ D、①和④11. 已知抛物线y=x2+mx+n与x轴只有一个公共点,且过点A(a,b),B(a-4,b),则b的值为( )A、4 B、2 C、6 D、912. 把四张形状大小完全相同的小长方形卡片(如图①),分两种不同形式不重叠的放在一个底面长为m,宽为n的长方形盒子底部(如图②、图③),盒子底面未被卡片覆盖的部分用阴影表示,设图②中阴影部分图形的周长为l1 , 图③中两个阴影部分图形的周长和为l2 , 若l1= l2 , 则m,n满足( )
A、①和② B、②和③ C、①和③ D、①和④11. 已知抛物线y=x2+mx+n与x轴只有一个公共点,且过点A(a,b),B(a-4,b),则b的值为( )A、4 B、2 C、6 D、912. 把四张形状大小完全相同的小长方形卡片(如图①),分两种不同形式不重叠的放在一个底面长为m,宽为n的长方形盒子底部(如图②、图③),盒子底面未被卡片覆盖的部分用阴影表示,设图②中阴影部分图形的周长为l1 , 图③中两个阴影部分图形的周长和为l2 , 若l1= l2 , 则m,n满足( ) A、m= n B、m= n C、m= n D、m= n
A、m= n B、m= n C、m= n D、m= n二、填空题(本题有6小题,每小题4分,共24分)
-
13. 二次根式 有意义,则x的取值范围是 。14. 分解因式: -9= .15. 一个不透明的布袋里装有2个红球和5个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为 。16. 如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
 17. 如图,已知半圆O的直径AB为12,OP=1,C为半圆上一点,连结CP。若将CP沿着射线AB方向平移至DE,若DE恰好与⊙O相切于点D,则平移的距离为 .
17. 如图,已知半圆O的直径AB为12,OP=1,C为半圆上一点,连结CP。若将CP沿着射线AB方向平移至DE,若DE恰好与⊙O相切于点D,则平移的距离为 . 18. 如图,在平面直角坐标系中,已知直线y=kx(k>0)分别交反比例函数y= 和y= 在第一象限的图象于点A、B,过点B作BD⊥x轴于点D,交y= 的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是 .
18. 如图,在平面直角坐标系中,已知直线y=kx(k>0)分别交反比例函数y= 和y= 在第一象限的图象于点A、B,过点B作BD⊥x轴于点D,交y= 的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是 .
三、解答题(本题有8小题,共78分,各小题都必须写出解答过程)
-
19. 计算:(-1)-1-|- |+sin30°+( )020. 在4x4的方格纸中,△ABC的顶点都在格点上。
 (1)、在图1中画出与△ABC全等且以BC为公共边的格点三角形(不与△ABC重合);(2)、在图2中画出与△ABC相似(不全等)且以AC为公共边的格点三角形(画出一个即可)。21. 2019届慈溪市初中学业水平考试体育考试选测项目除性别限定选择外的,其他项目为A、足球,B、50米跑,C、篮球运球投篮,D、跳绳。为了了解学生最喜欢选择哪一门项目,随机抽取部分学生进行调查,得到如下两幅不完整的统计图,请结合图中信息回答下列问题。
(1)、在图1中画出与△ABC全等且以BC为公共边的格点三角形(不与△ABC重合);(2)、在图2中画出与△ABC相似(不全等)且以AC为公共边的格点三角形(画出一个即可)。21. 2019届慈溪市初中学业水平考试体育考试选测项目除性别限定选择外的,其他项目为A、足球,B、50米跑,C、篮球运球投篮,D、跳绳。为了了解学生最喜欢选择哪一门项目,随机抽取部分学生进行调查,得到如下两幅不完整的统计图,请结合图中信息回答下列问题。 (1)、求抽取的学生的人数;(2)、补全条形统计图;(3)、在扇形统计图中,求出课程C所对应的圆心角度数。22. 双曲线y= (k>0)的图象如图所示,点A的坐标是(0,6),点B(a,0)(a>0)是x轴上的一个动点,G为线段AB的中点,把线段BG绕点B按顺时针方向旋转90°后得到线段BC,然后以AB,BC为边作矩形ABCD。
(1)、求抽取的学生的人数;(2)、补全条形统计图;(3)、在扇形统计图中,求出课程C所对应的圆心角度数。22. 双曲线y= (k>0)的图象如图所示,点A的坐标是(0,6),点B(a,0)(a>0)是x轴上的一个动点,G为线段AB的中点,把线段BG绕点B按顺时针方向旋转90°后得到线段BC,然后以AB,BC为边作矩形ABCD。 (1)、求C点坐标(用a的式子表示) ;(2)、若矩形ABCD水平向右平移二个单位,使双曲线y= 经过A,C两点,求a的值。23. 践行“低碳生活,绿色出行”理念,自行车成为人们喜爱的交通工具。其品牌共享自行车在慈溪的投放量自2017年起逐月增加,据统计,该品牌共享自行车1月份投放了640辆,3月份投放了1000辆。(1)、若该品牌共享自行车前4个月的投放量的月平均增长率相同,则4月份投放了多少辆?(2)、寒假里小明骑“共享单车”去离家2000米的慈溪银泰影视城观看电影,到了影视城发现假期优惠门票忘带了,于是骑车立即返回,已知返回的平均速度是来影视城时的平均速度的2倍,且途中时间少花了5分钟。求小明去影视城的平均速度?24. 如图,在△ABC中,AB=AC,以AC为直径作圆O,分别交BC于点D,交BA的延长线于点D,过点D作DH⊥AB于点H,连结DE交线段OA于点F。
(1)、求C点坐标(用a的式子表示) ;(2)、若矩形ABCD水平向右平移二个单位,使双曲线y= 经过A,C两点,求a的值。23. 践行“低碳生活,绿色出行”理念,自行车成为人们喜爱的交通工具。其品牌共享自行车在慈溪的投放量自2017年起逐月增加,据统计,该品牌共享自行车1月份投放了640辆,3月份投放了1000辆。(1)、若该品牌共享自行车前4个月的投放量的月平均增长率相同,则4月份投放了多少辆?(2)、寒假里小明骑“共享单车”去离家2000米的慈溪银泰影视城观看电影,到了影视城发现假期优惠门票忘带了,于是骑车立即返回,已知返回的平均速度是来影视城时的平均速度的2倍,且途中时间少花了5分钟。求小明去影视城的平均速度?24. 如图,在△ABC中,AB=AC,以AC为直径作圆O,分别交BC于点D,交BA的延长线于点D,过点D作DH⊥AB于点H,连结DE交线段OA于点F。 (1)、求证:DH是圆O的切线;(2)、若A为EH的中点,求 的值;(3)、若EA=EF=1,求圆O的半径.25. 一个三角形的三条边上各取一点,这三点构成的三角形叫做原三角形的内接三角形。△ABC中,∠A=∠B=30°,AC=4,△DEF是△ABC的内接三角形.
(1)、求证:DH是圆O的切线;(2)、若A为EH的中点,求 的值;(3)、若EA=EF=1,求圆O的半径.25. 一个三角形的三条边上各取一点,这三点构成的三角形叫做原三角形的内接三角形。△ABC中,∠A=∠B=30°,AC=4,△DEF是△ABC的内接三角形. (1)、如图①,已知DE∥AB,DF∥BC.
(1)、如图①,已知DE∥AB,DF∥BC.①若DF=EF,则DE=
②若△DEF是直角三角形,求CD的长(2)、如图②,若△DEF是等腰直角三角形,∠DFE=90°,D是AC中点,求tan∠AFD的值26. 如图1,在平面直角坐标系中,点M的坐标为(3,0),以点M为圆心,5为半径的圆与坐标轴分别交于点A、B、C、D. (1)、△AOD与△COB相似吗?为什么?(2)、如图2,弦DE交x轴于点P,且BP:DP=3:2,求tan∠EDA;(3)、如图3,过点D作圆M的切线,交x轴于点Q.点G是圆M上的动点,问比值 是否变化?若不变,请求出比值;若变化说明理由.
(1)、△AOD与△COB相似吗?为什么?(2)、如图2,弦DE交x轴于点P,且BP:DP=3:2,求tan∠EDA;(3)、如图3,过点D作圆M的切线,交x轴于点Q.点G是圆M上的动点,问比值 是否变化?若不变,请求出比值;若变化说明理由.