浙江省杭州市某重点初中2018年招生考试数学试卷
试卷更新日期:2019-06-10 类型:小升初真题
一、填空。(共18分)
-
1. 根据最新信息显示,目前中国人口总数约有1409517400人,改写成“亿”作单位的数约是亿,(保留两位小数)2. 1200g=kg 1.5L=mL3. “□86”是一个三位数,如果它是3的倍数,那么□里最大是。4. 下面直线上点A表示的数是 , 如果点B在1处,而点C是线段AB的中点,那么点C表示的数是.
 5. 比较大小。
5. 比较大小。a× a+ (a>0) 4.32÷ 4.32×0.25
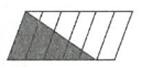
6. 将图中阴影部分面积与整个图形面积的关系分别用分数、百分数表示。=%
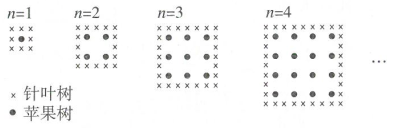
 7. 院子里有鸡和兔共12只,一共有34只脚,鸡和兔各有多少只?如果设鸡有x只,列出方程是。8. 如图,三角形从①旋转到②,是怎样旋转的?它是将三角形ABC。
7. 院子里有鸡和兔共12只,一共有34只脚,鸡和兔各有多少只?如果设鸡有x只,列出方程是。8. 如图,三角形从①旋转到②,是怎样旋转的?它是将三角形ABC。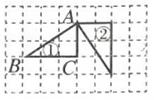 9. 如图,用铁皮正好能做成一个圆柱且没有浪费,已知小圆的直径是1dm,那么,做成的圆柱底面周长是dm,高是dm。
9. 如图,用铁皮正好能做成一个圆柱且没有浪费,已知小圆的直径是1dm,那么,做成的圆柱底面周长是dm,高是dm。
二、选择。(共16分)
-
10. 一袋面粉的质量标准是“25±0.25kg”,那么下面质量合格的是( )。A、24.70kg B、24.80kg C、25.30kg D、25.51kg11. 从下面四条线段中选出三条,能围成一个三角形的是( ).
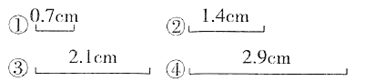 A、①②③ B、①②④ C、①③④ D、②③④12. 太阳到地球直线距离的平均值为149597870.7千米,光速大约是30万千米/秒,光从太阳到达地球大约需要( )秒.A、5 B、50 C、500 D、500013. 一个计算机芯片的实际尺寸是8mm×8mm,按一定比例所画的图如下图,图中所用的比例尺是( )。
A、①②③ B、①②④ C、①③④ D、②③④12. 太阳到地球直线距离的平均值为149597870.7千米,光速大约是30万千米/秒,光从太阳到达地球大约需要( )秒.A、5 B、50 C、500 D、500013. 一个计算机芯片的实际尺寸是8mm×8mm,按一定比例所画的图如下图,图中所用的比例尺是( )。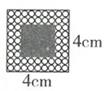 A、1:5 B、25:1 C、2:1 D、5:114. 王老师用28米长的木条给花圃做围栏,他想把花圃设计成以下四种造型,不能用28米的长木条围成的设计有( )种。
A、1:5 B、25:1 C、2:1 D、5:114. 王老师用28米长的木条给花圃做围栏,他想把花圃设计成以下四种造型,不能用28米的长木条围成的设计有( )种。 A、1 B、2 C、3 D、415. 从下面的数字卡片中任选两张求和,和可能是7,8,9,10,11,可能性最大的是( ).
A、1 B、2 C、3 D、415. 从下面的数字卡片中任选两张求和,和可能是7,8,9,10,11,可能性最大的是( ). A、7 B、8 C、9 D、1016. 数m、n、t在直线上的位置如图所示。下列式子结果与数t最接近的是( )。
A、7 B、8 C、9 D、1016. 数m、n、t在直线上的位置如图所示。下列式子结果与数t最接近的是( )。 A、n+m B、n×m C、m÷n D、n÷m17. 下面不能用方程“ x+x=60”来表示的是( )。A、
A、n+m B、n×m C、m÷n D、n÷m17. 下面不能用方程“ x+x=60”来表示的是( )。A、 B、
B、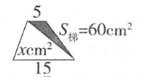 C、
C、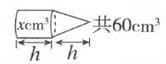 D、
D、
三、计算与操作。(共26分)
-
18. 直接写出得数。
687+95= 0.46+4.9=
0.5×2.4= 0.84÷0.7= 2.6× =
1.25× ×8=
19. 计算(写出必要过程)。①3.6+6.4×0.65
②20-3.69÷1.8
③
④18.8×4+1.2÷0.25
⑤118×
⑥(0.74-0.74× )÷0.37
20. 求未知数x。(1)、60%x+12×45%=7.8(2)、四、填空。(共14分)
-
21. 如下图,将△EDC放大一定比例成△ABC,直角△DCE的三条边分别是3cm、4cm、5cm。如果AB=6cm,那么AE=cm。
 22. 前几年,孙老师用8400元买了一台笔记本电脑,最近想更换一台价值12000元的新笔记本电脑,如果将旧电脑六折出售,孙老师再添元才能购得新电脑。23. 方叔叔在某投资平台上投资30万元,该项目年化收益率是11%(即每年收益是本金的11%),存期一年半,到期后可获利润万元。24. 一个圆柱形杯子中装着一些水,下图表示的是杯子中水的高度与体积的变化情况,请根据图,回答问题:
22. 前几年,孙老师用8400元买了一台笔记本电脑,最近想更换一台价值12000元的新笔记本电脑,如果将旧电脑六折出售,孙老师再添元才能购得新电脑。23. 方叔叔在某投资平台上投资30万元,该项目年化收益率是11%(即每年收益是本金的11%),存期一年半,到期后可获利润万元。24. 一个圆柱形杯子中装着一些水,下图表示的是杯子中水的高度与体积的变化情况,请根据图,回答问题: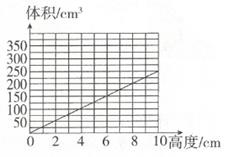 (1)、如果水的高度是7cm,水的体积是cm3。(2)、如果水的体积是350cm3 , 此时水的高度是cm。25. 下图阴影部分的面积是cm2。
(1)、如果水的高度是7cm,水的体积是cm3。(2)、如果水的体积是350cm3 , 此时水的高度是cm。25. 下图阴影部分的面积是cm2。 26. 有甲、乙两个长方体容器(如图),把一瓶水倒入两个容器后,要使得两个容器内水的体积相同,甲、乙两个容器中水的高度比应该是:。
26. 有甲、乙两个长方体容器(如图),把一瓶水倒入两个容器后,要使得两个容器内水的体积相同,甲、乙两个容器中水的高度比应该是:。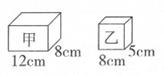 27. 图中两个物体都是用棱长为1厘米的正方体搭成的,这两个物体的表面积相差cm2。
27. 图中两个物体都是用棱长为1厘米的正方体搭成的,这两个物体的表面积相差cm2。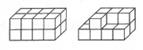
五、解决问题。(共26分)
-
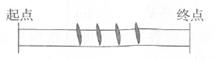
28. 体育课上进行40m的跨栏运动。跑道上等距放置了4个栏架,每两个栏架之间距离为5.5m。
 (1)、跑道起点与第一个栏架之间的距离是12m,莫老师用卷尺测量后再放置栏架,如果将卷尺的“0m”与起点重合,第4个栏架在卷尺的多少米处?(2)、小宇完成40m跨栏需用时9.7秒,如果没有栏架,小宇跑40m只需用时8.1秒。每个跨栏动作需要多少秒?29. 已知三角形ABC的三个顶点的位置分别是A(5,3),B(-2,0),C(5,0)。如果每个单位长度是1cm,那么,三角形ABC绕BC旋转一周所得到的图形的体积是多少?30. 大正方形的周长是36厘米,a:b=1:2,则小正方形(阴影部分)的面积是多少平方厘米?
(1)、跑道起点与第一个栏架之间的距离是12m,莫老师用卷尺测量后再放置栏架,如果将卷尺的“0m”与起点重合,第4个栏架在卷尺的多少米处?(2)、小宇完成40m跨栏需用时9.7秒,如果没有栏架,小宇跑40m只需用时8.1秒。每个跨栏动作需要多少秒?29. 已知三角形ABC的三个顶点的位置分别是A(5,3),B(-2,0),C(5,0)。如果每个单位长度是1cm,那么,三角形ABC绕BC旋转一周所得到的图形的体积是多少?30. 大正方形的周长是36厘米,a:b=1:2,则小正方形(阴影部分)的面积是多少平方厘米? 31. 已知一个内直径是8cm的饮料瓶内还剩饮料的高度是6cm,要解决“这个瓶子的容积是多少”这个问题,可以怎么解决?把你想到的办法表达清楚,不必解答。
31. 已知一个内直径是8cm的饮料瓶内还剩饮料的高度是6cm,要解决“这个瓶子的容积是多少”这个问题,可以怎么解决?把你想到的办法表达清楚,不必解答。