2016-2017学年云南省楚雄州姚安一中高二下学期期中数学试卷(理科)
试卷更新日期:2017-05-27 类型:期中考试
一、选择题:
-
1. 设全集U=R,集合A={x|x>0},B={x|x2﹣x﹣2<0},则A∩(∁UB)=( )A、(0,2] B、(﹣1,2] C、[﹣1,2] D、[2,+∞)2. 复数(1﹣ i)•i的虚部是( )A、1 B、﹣1 C、i D、﹣i3. 已知| |=1,| |=2,向量 与 的夹角为60°,则| + |=( )A、 B、 C、1 D、24. 等差数列{an}中,若a1+a4+a7=39,a3+a6+a9=27,则前9项的和S9等于( )A、66 B、99 C、144 D、2975. 在△ABC中,a2=b2+c2+ bc,则∠A等于( )A、60° B、45° C、120° D、150°6. 在复平面内,复数z= 对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 已知抛物线x2=2y的焦点与椭圆 =1的一个焦点重合,则m=( )A、 B、 C、﹣ D、﹣8. 要得到函数y=cos(2x+1)的图象,只要将函数y=cos2x的图象( )A、向左平移1个单位 B、向右平移1个单位 C、向左平移 个单位 D、向右平移 个单位9. 已知双曲线 =1(a>0,b>0)的离心率为2,则双曲线的渐近线方程为( )A、 B、 C、 D、10. 已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+lnx,则f′(1)=( )A、﹣e B、﹣1 C、1 D、e11. 设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )
 A、
A、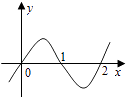 B、
B、 C、
C、 D、
D、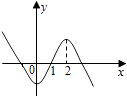 12. 函数y= sin(x+ )+cos( ﹣x)的最大值为( )A、 B、 C、 D、
12. 函数y= sin(x+ )+cos( ﹣x)的最大值为( )A、 B、 C、 D、二、填空题:
-
13. 已知变量x,y满足约束条件 则z=2x+y的最大值为 .14. 设tanα=3,则 = .15. 函数f(x)的图象在x=2处的切线方程为2x+y﹣3=0,则f(2)+f'(2)= .16. 已知f(x)=3x2+2x+1,若 f(x)dx=2f(a),则a= .
三、解答题:
-
17. 已知函数f(x)=ex(x2+x+1),求函数f(x)的单调区间及极值.18. 已知a,b,c分别是△ABC的角A,B,C所对的边,且c=2,C= .(1)、若△ABC的面积等于 ,求a,b;(2)、若sinC+sin(B﹣A)=2sin2A,求A的值.19. 在等比数列{an}中,a1=2,a4=16(1)、求数列{an}的通项公式;(2)、令 ,n∈N* , 求数列{bn}的前n项和Sn .20. 如图,在直三棱柱A1B1C1﹣ABC中,AB=AC=AA1 , ,点D是BC的中点.
(I)求证:AD⊥平面BCC1B1;
(II)求证:A1B∥平面ADC1;
(III)求二面角A﹣A1B﹣D的余弦值.
