2016-2017学年河北省邯郸市大名县、永年区、磁县、邯山区联考高二下学期期中数学试卷（理科）

试卷更新日期：2017-05-27 类型：期中考试

进入出卷网下载

一、选择题

1. 已知i是虚数单位，则 $\frac{i}{1 - i}$ =（）

A、 $\frac{1}{2}$ + $\frac{1}{2} i$ B、﹣ $\frac{1}{2}$ + $\frac{1}{2} i$ C、 $\frac{1}{2}$ ﹣ $\frac{1}{2} i$ D、﹣ $\frac{1}{2}$ ﹣ $\frac{1}{2} i$

查看试题解析
2. 命题“∀x∈R，x²+2^x﹣1＜0”的否定是（）

A、∀x∈R，x²+2^x﹣1≥0 B、∃x∈R，x²+2^x﹣1＜0 C、∃x∈R，x²+2^x﹣1≥0 D、∃x∈R，x²+2^x﹣1＞0

查看试题解析
3. 用反证法证明命题：“已知a、b是自然数，若a+b≥3，则a、b中至少有一个不小于2”提出的假设应该是（）

A、a、b都小于2 B、a、b至少有一个不小于2 C、a、b至少有两个不小于2 D、a、b至少有一个小于2

查看试题解析
4. 若向量 $\vec{a}$ =（1，λ，2）， $\vec{b}$ =（2，﹣1，2），且 $\vec{a}$ 与 $\vec{b}$ 的夹角余弦值为 $\frac{8}{9}$ ，则λ等于（）

A、2 B、﹣2 C、﹣2或 $\frac{2}{55}$ D、2或﹣ $\frac{2}{55}$

查看试题解析
5. 若曲线y=x³的切线方程为y=kx+2，则k=（）

A、﹣1 B、1 C、﹣3 D、3

查看试题解析
6. 已知随机变量X～B（6，0.4），则当η=﹣2X+1时，D（η）=（）

A、﹣1.88 B、﹣2.88 C、5.76 D、6.76

查看试题解析
7. 从5位男数学教师和4位女数学教师中选出3位教师派到3个班担任班主任（每班1位班主任），要求这3位班主任中男女教师都有，则不同的选派方案共有（）

A、210 B、420 C、630 D、840

查看试题解析
8. 抛物线x²=2y和直线y=x+4所围成的封闭图形的面积是（）

A、16 B、18 C、20 D、22

查看试题解析
9. 设F₁和F₂为双曲线 $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的两个焦点，若F₁ ， F₂ ， P（0，2b）是正三角形的三个顶点，则双曲线的渐近线方程是（）

A、y=± $\frac{\sqrt{3}}{3}$ x B、y=± $\sqrt{3}$ x C、y=± $\frac{\sqrt{21}}{7}$ x D、y=± $\frac{\sqrt{21}}{3}$ x

查看试题解析
10. 如图，AB=AC=BD=1，AB⊂面M，AC⊥面M，BD⊥AB，BD与面M成30°角，则C、D间的距离为（）

A、1 B、2 C、 $\sqrt{2}$ D、 $\sqrt{3}$

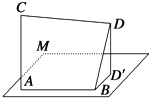查看试题解析
11. 已知（1﹣3x）⁹=a₀+a₁x+a₂x²+…+a₉x⁹ ，则|a₀|+|a₁|+|a₂|+…+|a₉|等于（）

A、2⁹ B、4⁹ C、3⁹ D、1

查看试题解析
12. 函数g（x）是奇函数f（x）（x∈R）的导函数，f（1）=0，当x＞0时，xg（x）﹣f（x）＜0，则使得f（x）＜0成立的x的取值范围是（）

A、（﹣∞，﹣1）∪（0，1） B、（0，1）∪（1，+∞） C、（﹣∞，﹣1）∪（﹣1，0） D、（﹣1，0）∪（1，+∞）

查看试题解析

二、填空题

13. 将一个大正方形平均分成9个小正方形，向大正方形区域随机地投掷一个点（每次都能投中），投中最左侧3个小正方形区域的事件记为A，投中最上面3个小正方形或正中间的1个小正方形区域的事件记为B，则P（A|B）= ．

查看试题解析
14. 学校艺术节对同一类的A，B，C，D四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品预测如下：
甲说：“是C或D作品获得一等奖”；
乙说：“B作品获得一等奖”；
丙说：“A，D两项作品未获得一等奖”；
丁说：“是C作品获得一等奖”．
若这四位同学中只有两位说的话是对的，则获得一等奖的作品是．

查看试题解析
15. 已知下列三个命题：
①若一个球的半径缩小到原来的 $\frac{1}{2}$ ，则其体积缩小到原来的 $\frac{1}{8}$ ；
②若两组数据的平均数相等，则它们的标准差也相等；
③直线x+y+1=0与圆x²+y²= $\frac{1}{2}$ 相切．
其中真命题的序号是．

查看试题解析
16. 已知点P（a，0），若抛物线y²=4x上任一点Q都满足|PQ|≥|a|，则a的取值范围是．

查看试题解析

三、解答题

17. 已知命题p：对于m∈[﹣1，1]，不等式a²﹣5a﹣3≥ $\sqrt{m^{2} + 8}$ 恒成立；命题q：不等式x²+ax+2＜0有解，若p∨q为真，且p∧q为假，求a的取值范围．

查看试题解析
18. 已知函数 $f (x) = \frac{1}{2} x^{2} - a x + (a - 1) \ln x$ ．

(1)、当a=2，求函数f（x）的图象在点（1，f（1））处的切线方程；

(2)、当a＞2时，求函数f（x）的单调区间．

查看试题解析
19. 如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且∠BCD=∠BCE= $\frac{π}{2}$ ，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG=2．

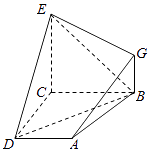(1)、证明：AG∥平面BDE．

(2)、求平面BDE和平面ADE所成锐二面角的余弦值．

查看试题解析
20. 现有4个人去参加娱乐活动，该活动有甲、乙两个游戏可供参加者选择．为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏．

(1)、求这4个人中恰有2人去参加甲游戏的概率；

(2)、求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率；

(3)、用X，Y分别表示这4个人中去参加甲、乙游戏的人数，记ξ=|X﹣Y|，求随机变量ξ的分布列与数学期望Eξ．

查看试题解析
21. 已知f（x）=e^x﹣ax﹣1．

(1)、求f（x）的单调递增区间；

(2)、若f（x）在定义域R内单调递增，求a的取值范围．

查看试题解析
22. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率 $e = \frac{\sqrt{3}}{2}$ ，连接椭圆的四个顶点得到的菱形的面积为4．

(1)、求椭圆的方程；

(2)、设直线l与椭圆相交于不同的两点A，B，已知点A的坐标为（﹣a，0），点Q（0，y₀）在线段AB的垂直平分线上，且 $\vec{Q A} \cdot \vec{Q B} = 4$ ，求y₀的值．

查看试题解析