2019年高考理数真题试卷(天津卷)
试卷更新日期:2019-06-09 类型:高考真卷
一、选择题:本卷共8小题,每小题5分,共40分。
-
1. 设集合 ,则 ( )A、{2} B、{2,3} C、{-1,2,3} D、{1,2,3,4}2. 设变量 满足约束条件 则目标函数 的最大值为( )A、2 B、3 C、5 D、63. 设 ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件4. 阅读下边的程序框图,运行相应的程序,输出 的值为( )
 A、5 B、8 C、24 D、295. 已知抛物线 的焦点为 ,准线为 ,若 与双曲线 的两条渐近线分别交于点 和点 ,且 ( 为原点),则双曲线的离心率为( )A、 B、 C、 D、6. 已知 , , ,则 的大小关系为( )A、 B、 C、 D、7. 已知函数 是奇函数,将 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为 .若 的最小正周期为 ,且 ,则 ( )A、 B、 C、 D、8. 已知 ,设函数 若关于 的不等式 在 上恒成立,则 的取值范围为( )A、 B、 C、 D、
A、5 B、8 C、24 D、295. 已知抛物线 的焦点为 ,准线为 ,若 与双曲线 的两条渐近线分别交于点 和点 ,且 ( 为原点),则双曲线的离心率为( )A、 B、 C、 D、6. 已知 , , ,则 的大小关系为( )A、 B、 C、 D、7. 已知函数 是奇函数,将 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为 .若 的最小正周期为 ,且 ,则 ( )A、 B、 C、 D、8. 已知 ,设函数 若关于 的不等式 在 上恒成立,则 的取值范围为( )A、 B、 C、 D、二、填空题:本大题共6小题,每小题5分,共30分.
-
9. 是虚数单位,则 的值为.10. 是展开式中的常数项为.11. 已知四棱锥的底面是边长为 的正方形,侧棱长均为 .若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为.12. 设 ,直线 和圆 ( 为参数)相切,则 的值为.13. 设 ,则 的最小值为.14. 在四边形 中, ,点 在线段 的延长线上,且 ,则 .
三、解答题:本大题共6小题,共80分.
-
15. 在 中,内角 所对的边分别为 .已知 , .
(Ⅰ)求 的值;
(Ⅱ)求 的值.
16. 设甲、乙两位同学上学期间,每天7:30之前到校的概率均为 .假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.(Ⅰ)用 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量 的分布列和数学期望;
(Ⅱ)设 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件 发生的概率.
17. 如图, 平面 , , .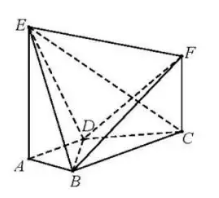
(Ⅰ)求证: 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值;
(Ⅲ)若二面角 的余弦值为 ,求线段 的长.