2019年高考文数真题试卷（全国Ⅱ卷）

试卷更新日期：2019-06-09 类型：高考真卷

进入出卷网下载

一、选择题：本题共12小题，每小题5分，共60分。

1. 已知集合A={x|x>-1}，B={x|x<2}，则A∩B=（）

A、（-1，+∞） B、（ -∞，2） C、（ -1，2） D、 $ϕ$

查看试题解析
2. 设z=i（2+i），则 $\bar{z}$ =（）

A、1+2i B、-1+2i C、1-2i D、-1-2i

查看试题解析
3. 已知向量 $\vec{a}$ =（2，3）， $\vec{b}$ =（3，2），则| $\vec{a}$ - $\vec{b}$ |=（）

A、 $\sqrt{2}$ B、2 C、5 $\sqrt{2}$ D、50

查看试题解析
4. 生物实验室有5只兔子，其中只有3只测量过某项指标。若从这5只兔子中随机取出3只，则恰有2只测量过该指标的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{5}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
5. 在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测。
甲：我的成绩比乙高。

乙：丙的成绩比我和甲的都高。

丙：我的成绩比乙高。

成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为（）

A、甲、乙、丙 B、乙、甲、丙 C、丙、乙、甲 D、甲、丙、乙

查看试题解析
6. 设f（x）为奇函数，且当x≥0时，f（x）= $e^{x}$ -1，则当x<0时，f（x）=（）

A、 $e^{- x}$ -1 B、 $e^{- x}$ +1 C、- $e^{- x}$ -1 D、- $e^{- x}$ +1

查看试题解析
7. 设α，β为两个平面，则α∥β的充要条件是（）

A、α内有无数条直线与β平行 B、α内有两条相交直线与β平行 C、α，β平行于同一条直线 D、α，β垂直于同一平面

查看试题解析
8. 若 $x_{1} = \frac{π}{4}$ ， $x_{2} = \frac{3 π}{4}$ 是函数f（x）= sinωx（ω>0）两个相邻的极值点，则ω（）

A、2 B、 $\frac{3}{2}$ C、1 D、 $\frac{1}{2}$

查看试题解析
9. 若抛物线y²=2px(p>0)的焦点是椭圆 $\frac{x^{2}}{3 p} + \frac{y^{2}}{p} = 1$ 的一个焦点，则p=（）

A、2 B、3 C、4 D、8

查看试题解析
10. 曲线y=2sinx+cosx在点（π，-1）处的切线方程为（）

A、x-y-π-1=0 B、2x-y-2π-1=0 C、2x+y-2π+1=0 D、x+y-π+1=0

查看试题解析
11. 已知α∈(0, $\frac{π}{2}$ )，2sin2α=cos2α+1，则sinα=（）

A、 $\frac{1}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
12. 设F为双曲线C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的右焦点， $O$ 为坐标原点，以 $O F$ 为直径的圆与圆 $x^{2} + y^{2} = a^{2}$ 交于P，Q两点.若 $| P Q | = | O F |$ ，则C的离心率为（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

查看试题解析

二、填空题：本题共4小题，每小题5分，共20分

13. 若变量x，y满足约束条件 ${\begin{matrix} \begin{array}{l} 2 x + 3 y - 6 \geq 0 \\ x + y - 3 \leq 0 \end{array} \\ y - 2 \leq 0 \end{matrix}$ ，则，z=3x-y的最大值是。

查看试题解析
14. 我国高铁发展迅速，技术先进.经统计，在经停某站的高铁列车中，有10个车次的正点率为0.97，有20个车次的正点率为0.98，有10个车次的正点率为0.99，则经停该站高铁列车所有车次的平均正点率的估计值为.

查看试题解析
15. △ABC的内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，知 $b s i n A + a c o s B = 0$ ，则 $B$ =

查看试题解析
16. 中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1.则该半正多面体共有个面，其棱长为.

查看试题解析

三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。

17. 如图，长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面 $A B C D$ 是正方形，点 $E$ 在棱 $A A_{1}$ 上， $B E ⊥ E C_{1}$ 。

(1)、证明： $B E ⊥ 平面 E B_{1} C_{1}$ ；

(2)、若 $A E = A_{1} E$ ， $A B = 3$ ，求四棱锥 $E - B B_{1} C_{1} C$ 的体积。

查看试题解析
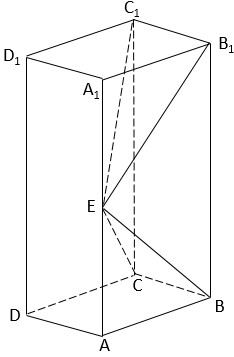18. 已知 ${a_{n}}$ 是各项均为正数的等比数列， $a_{1} = 2$ ， $a_{3} = 2 a_{2} + 16$ 。

(1)、求 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = l o g_{2} a_{n}$ ，求数列{ $b_{n}$ }的前n项和。

查看试题解析
19. 某行业主管部门为了解本行业中小企业的生产情况，随机调查了100个企业，得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表。
y的分组 [-0.20，0) [0，0.20) [0.20，0.40) [0.40，0.60) [0.60，0.80)
企业数 2 24 53 14 7
附： $\sqrt{74} \approx 8.602$

(1)、分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;

(2)、求这类企业产值增长率的平均数与标准差的估计值（同一组中的数据用该组区间的中点值为代表）.（精确到0.01）

查看试题解析
20. 已知 $F_{1}, F_{2}$ 是椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$ 的两个焦点， $P$ 为 $C$ 上的点， $O$ 为坐标原点。

(1)、若 $△ P O F_{2}$ 为等边三角形，求 $C$ 的离心率；

(2)、如果存在点P，使得 $P F_{1} ⊥ P F_{2}$ ，且 $△ F_{1} P F_{2}$ 的面积等于16，求 $b$ 的值和a的取值范围。

查看试题解析
21. 已知函数 $f (x) = (x - 1) l n x - x - 1$ ，证明：

(1)、 $f (x)$ 存在唯一的极值点；

(2)、 $f (x) = 0$ 有且仅有两个实根，且两个实根互为倒数.

查看试题解析

四、选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。

22. [选修4-4：坐标系与参数方程]在极坐标系中，O为极点，点 $M (ρ_{0} ， θ_{0}) (ρ_{0} > 0)$ 在曲线 $C ： ρ = 4 s i n θ$ 上，直线l过点 $A (4 ， 0)$ 且与 $O M$ 垂直，垂足为P.

(1)、当 $θ_{0} = \frac{π}{3}$ 时，求 $ρ_{0}$ 及l的极坐标方程；

(2)、当M在C上运动且P在线段OM上时，求P点轨迹的极坐标方程.

查看试题解析
23. 已知 $f (x) = | x - a | x + | x - 2 | (x - a) .$

(1)、当 $a = 1$ 时，求不等式 $f (x) < 0$ 的解集；

(2)、若 $x \in (- \infty ， 1 ）$ 时， $f (x) < 0$ ，求 $a$ 的取值范围.

查看试题解析

y的分组	[-0.20，0)	[0，0.20)	[0.20，0.40)	[0.40，0.60)	[0.60，0.80)
企业数	2	24	53	14	7

2019年高考文数真题试卷（全国Ⅱ卷）

一、选择题：本题共12小题，每小题5分，共60分。

二、填空题：本题共4小题，每小题5分，共20分

三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。

四、选考题 ：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。

四、选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。