2019年高考文数真题试卷（北京卷）

试卷更新日期：2019-06-08 类型：高考真卷

进入出卷网下载

一、选择题共8小题，每小题5分，共40分.

1. 已知集合A={x|-1<x<2}，B={x|x>1}，则AUB=（）

A、（-1，1） B、（1，2） C、（-1，+∞） D、（1，+∞）

查看试题解析
2. 已知复数z=2+i，则 $z · \bar{z}$ =（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、3 D、5

查看试题解析
3. 下列函数中，在区间（0，+∞）上单调递增的是（）

A、 $y = x^{\frac{1}{2}}$ B、y=2^-x C、 $y = \log_{\frac{1}{2}} x$ D、 $y = \frac{1}{x}$

查看试题解析
4. 执行如图所示的程序框图，输出的s值为（）

A、1 B、2 C、3 D、4

查看试题解析
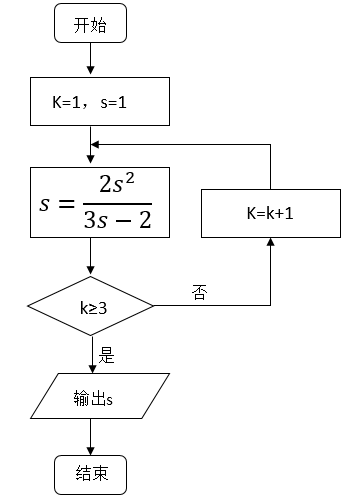5. 已知双曲线 $\frac{x^{2}}{a^{2}} - y^{2} = 1$ （a>0）的离心率是 $\sqrt{5}$ ，则a=（）

A、 $\sqrt{6}$ B、4 C、2 D、 $\frac{1}{2}$

查看试题解析
6. 设函数f（x）=cosx+bsinx（b为常数），则“b=0”是“f（x）为偶函数”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
7. 在天文学中，天体的明暗程度可以用星等或亮度来描述。两颗星的星等与亮度满足m₂-m₁= $\frac{5}{2} \lg \frac{E_{1}}{E_{2}}$ ，其中星等为m_k的星的亮度为E_k（k=1，2）.已知太阳的星等是-26.7，天狼星的星等是-1.45，则太阳与天狼星的亮度的比值为（）

A、10^10.1 B、10.1 C、lg10.1 D、10^-10.1

查看试题解析
8. 如图，A，B是半径为2的圆周上的定点，P为圆周上的动点，∠APB是锐角，大小为β.图中阴影区域的面积的最大值为（）

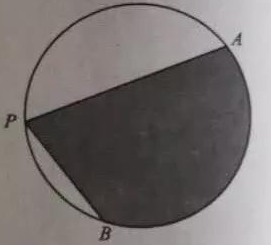A、4β+4cosβ B、4β+4sinβ C、2β+2cosβ D、2β+2sinβ

查看试题解析

二、填空题共6小题，每小题5分，共30分，

9. 已知向量 $\vec{a}$ =（-4.3）， $\vec{b}$ =（6，m），且 $\vec{a} ⊥ \vec{b}$ ，则m=.

查看试题解析
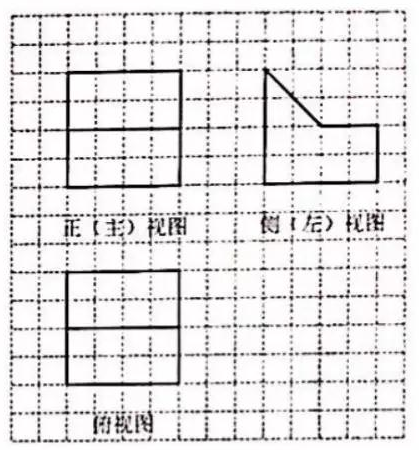
10. 若x，y满足 ${\begin{cases} x \leq 2 \\ y \geq - 1 \\ 4 x - 3 y + 1 \geq 0 \end{cases}$ .则y-x的最小值为，最大值为.

查看试题解析
11. 设抛物线y²=4x的焦点为F，准线为l.则以F为圆心，且与l相切的圆的方程为.

查看试题解析
12. 某几何体是由一个正方体去掉一个四棱柱所得.其三视图如图所示.如果网格纸上小正方形的边长为1.那么该几何体的体积为.

查看试题解析
13. 已知l，m是平面α外的两条不同直线.给出下列三个论断：
①l⊥m：②m∥α：③l⊥α.

以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：。

查看试题解析
14. 李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒。为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x元。每笔订单顾客网上支付成功后，李明会得到支付款的80%.
①当x=10时，顾客一次购买草莓和西瓜各1盒，需要支付元；
②在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为。

查看试题解析

三、解答题共6小题，共80分.

15. 在△ABC中，a=3，b-c=2，cosB=- $\frac{1}{2}$ .
（I）求b，c的值：

（II）求sin（B+C）的值.

查看试题解析
16. 设{a_n}是等差数列，a₁=-10，且a₂+10，a₃+8，a₄+6成等比数列.
（I）求{a_n}的通项公式；

（Ⅱ）记{a_n}的前n项和为S_n ，求S_n的最小值.

查看试题解析
17. 改革开放以来，人们的支付方式发生了巨大转变.近年来，移动支付已成为主要支付方式之一.为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校所有的1000名学生中随机抽取了100人，发现样本中A，B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：

支付金额

支付方式

不大于2000元

大于2000元

仅使用A

27人

3人

仅使用B

24人

1人

（I）估计该校学生中上个月A，B两种支付方式都使用的人数；

（II）从样本仅使用B的学生中随机抽取1人，求该学生上个月支付金额大于2000元的概率；

（III）已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中，随机抽查1人，发现他本月的支付金额大于2000元，结合（II）的结果，能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化？说明理由.

查看试题解析
18. 如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点.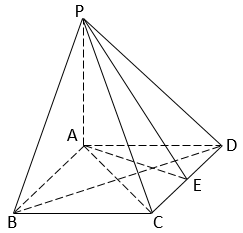

（Ⅰ）求证：BD⊥平面PAC；
（Ⅱ）若∠ABC=60°，求证：平面PAB⊥平面PAE；
（Ⅲ）棱PB上是否存在点F，使得CF∥平面PAE？说明理由.

查看试题解析
19. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 的右焦点为（1.0），且经过点A（0，1）.
（I）求椭圆C的方程；

（II）设O为原点，直线l：y=kx+t（t≠±1）与椭圆C交于两个不同点P，Q，直线AP与x轴交于点M，直线AQ与x轴交于点N，|OM|·|ON|=2，求证：直线l经过定点.

查看试题解析
20. 已知函数f（x）= $\frac{1}{4}$ x³-x²+x.
（I）求曲线y=f（x）的斜率为1的切线方程；
（II）当x∈[-2，4]时，求证：x-6≤f（x）≤x；
（IlI）设F（x）=|f（x）-（x+a）|（a∈R），记F（x）在区间[-2，4]上的最大值为M（a）. 当M（a）最小时，求a的值.

查看试题解析