2019年高考理数真题试卷（北京卷）

试卷更新日期：2019-06-08 类型：高考真卷

进入出卷网下载

一、选择题共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。

1. 已知复数z=2+i，则 $z · \bar{z}$ =（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、3 D、5

查看试题解析
2. 执行如图所示的程序框图，输出的s值为（）

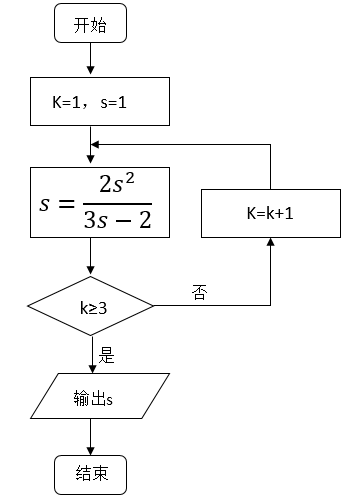A、1 B、2 C、3 D、4

查看试题解析
3. 已知直线l的参数方程为 ${\begin{cases} x = 1 + 3 t \\ y = 2 + 4 t \end{cases}$ （t为参数），则点（1，0）到直线l的距离是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{4}{5}$ D、 $\frac{6}{5}$

查看试题解析
4. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a>b>0）的离心率为 $\frac{1}{2}$ ，则（）

A、a²=2b² B、3a²=4b² C、a=2b D、3a=4b

查看试题解析
5. 若x，y满足|x|≤1-y，且y≥-1.则3x+y的最大值为（）

A、-7 B、1 C、5 D、7

查看试题解析
6. 在天文学中，天体的明暗程度可以用星等或亮度来描述。两颗星的星等与亮度满足m₂-m₁= $\frac{5}{2} \lg \frac{E_{1}}{E_{2}}$ ，其中星等为m_k的星的亮度为E_k（k=1，2）.已知太阳的星等是-26.7，天狼星的星等是-1.45，则太阳与天狼星的亮度的比值为（）

A、10^10.1 B、10.1 C、lg10.1 D、10^-10.1

查看试题解析
7. 设点A，B，C不共线，则“ $\vec{A B}$ 与 $\vec{A C}$ 的夹角为锐角”是“| $\vec{A B}$ + $\vec{A C}$ |>| $\vec{B C}$ |”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
8. 数学中有许多形状优美、寓意美好的曲线，曲线C：x²+y²=1+|x|y就是其中之一（如图）.给出下列三个结论：

①曲线C恰好经过6个整点（即横、纵坐标均为整数的点）；

②曲线C上任一点到原点的距离都不超过 $\sqrt{2}$ ；

③曲线C所围成的“心形”区域的面积小于3.

其中，所有正确结论的序号是（）

A、① B、② C、①② D、①②③

查看试题解析

二、填空题共6小题，每小题5分，共30分。

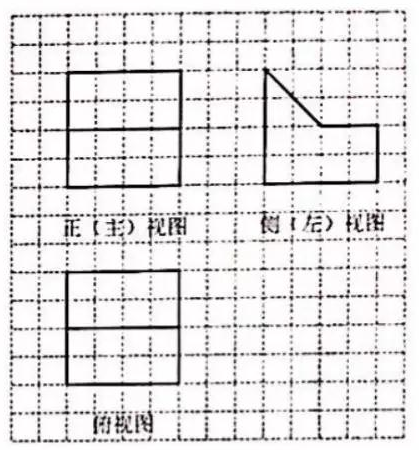
9. 函数f（x）=sin²2x的最小正周期是.

查看试题解析
10. 设等差数列{a_n}的前n项和为S_n.若a₂=-3，S₅=-10，则a₅= ， S_n的最小值为.

查看试题解析
11. 某几何体是由一个正方体去掉一个四棱柱所得.其三视图如图所示.如果网格纸上小正方形的边长为1.那么该几何体的体积为.

查看试题解析
12. 已知l，m是平面α外的两条不同直线.给出下列三个论断：
①l⊥m：②m∥α：③l⊥α.

以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：。

查看试题解析
13. 设函数f（x）=e^x+ae^-x（a为常数）。若f（x）为奇函数，则a=：若f（x）是R上的增函数，则a的取值范围是.

查看试题解析
14. 李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒。为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x元。每笔订单顾客网上支付成功后，李明会得到支付款的80%.
①当x=10时，顾客一次购买草莓和西瓜各1盒，需要支付元；
②在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为。

查看试题解析

三、解答题共6小题，共80分。

15. 在△ABC中，a=3，b-c=2，cosB=- $\frac{1}{2}$ .
（I）求b，c的值；
（II）求sin（B-C）的值.

查看试题解析
16. 如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3。E为PD的中点，点F在PC上，且 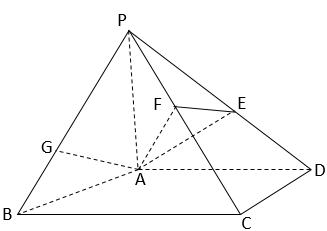$\frac{P F}{P C} = \frac{1}{3}$ .

（I）求证：CD⊥平面PAD；
（II）求二面角F-AE-P的余弦值；
（III）设点G在PB上，且 $\frac{P G}{P B} = \frac{2}{3}$ .判断直线AG是否在平面AEF内，说明理由。

查看试题解析

17. 改革开放以来，人们的支付方式发生了巨大转变。近年来，移动支付已成为主要支付方式之一。为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校学生中随机抽取了100人，发现样本中A，B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：

支付金额（元）

支付方式

（0，1000]

（1000，2000]

大于2000

仅使用A

18人

9人

3人

仅使用B

10人

14人

1人

（I）从全校学生中随机抽取1人，估计该学生上个月A，B两种支付方式都使用的概率；

（II）从样本仅使用A和仅使用B的学生中各随机抽取1人，以X表示这2人中上个月支付金额大于1000元的人数，求X的分布列和数学期望；

（III）已知上个月样本学生的支付方式在本月没有变化。现从样本仅使用A的学生中，随机抽查3人，发现他们本月的支付金额都大于2000元，根据抽查结果，能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化？说明理由.

查看试题解析

18. 已知抛物线C：x²=-2py经过点（2，-1）.
（I）求抛物线C的方程及其准线方程；

（II）设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M，N，直线y=-1分别交直线OM，ON于点A和点B.求证：以AB为直径的圆经过y轴上的两个定点.

查看试题解析
19. 已知函数f（x）= $\frac{1}{4}$ x³-x²+x.
（I）求曲线y=f（x）的斜率为1的切线方程；
（II）当x∈[-2，4]时，求证：x-6≤f（x）≤x；
（IlI）设F（x）=|f（x）-（x+a）|（a∈R），记F（x）在区间[-2，4]上的最大值为M（a）. 当M（a）最小时，求a的值.

查看试题解析
20. 已知数列{a_n}，从中选取第i₁项、第i₂项…第i_m项（i₁<i₂<…<i_m）.若a_i1<a_i2<…<a_im.则称新数列a_i1 ， a_i2 ， …，a_im.为{a_n}的长度为m的递增子列.规定：数列{a_n}的任意一项都是{a_n}的长度为1的递增子列.
（I）写出数列1，8，3，7，5，6，9的一个长度为4的递增子列；
（II）已知数列{a_n}的长度为P的递增子列的末项的最小值为a_m0 ，长度为q的递增子列的末项的最小值为a_n0 ，若p<q，求证：a_m0<a_n0；
（III）设无穷数列{a_n}的各项均为正整数，且任意两项均不相等。若{a_n}的长度为s的递增子列末项的最小值为2s-1，且长度为s末项为2s-1的递增子列恰有2^s-1个（s=1.2.…），求数列{a_n}的通项公式。

查看试题解析