2019年高考文数真题试卷(全国Ⅰ卷)
试卷更新日期:2019-06-08 类型:高考真卷
一、选择题:本题共12小题,每小题5分,共60分。在每小题检出的四个选项中,只有一项是符合题目要求的。
-
1. 设z= ,则|z|=( )
A、2 B、 C、 D、1 -
2. 已知集合U= ,A= ,B= 则 =( )A、 B、 C、 D、
-
3. 已知a=log20.2,b= ,c= ,则( )A、a<b<c B、a<c<b C、c<a<b D、b<c<a
-
4. 古希腊吋期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ,称为黄金分割比例),著名的“断臂维纳斯“便是如此。此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度也是 。若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是( )
 A、165cm B、175cm C、185cm D、190cm
A、165cm B、175cm C、185cm D、190cm -
5. 函数f(x)= 在[- , ]。的图像大致为( )A、
 B、
B、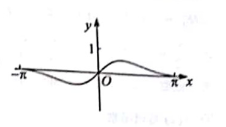 C、
C、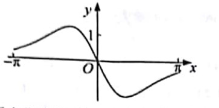 D、
D、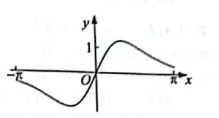
-
6. 某学校为了解1000名新生的身体素质,将这些学生编号为1,2,……,1000。从这些新生中用系统抽样方法等距抽取100名学生进行体质测验,若46号学生被抽到,则下面4名学生中被抽到的是( )
A、8号学生 B、200号学生 C、616号学生 D、815号学生 -
7. tan255°=( )A、 B、 C、 D、
-
8. 已知非零向量 , 满足| |=2| |,且 ,则 与 的夹角为( )A、 B、 C、 D、
-
9. 下图是求 的程序框图,图中空白框中应填入( )
 A、A= B、A=2+ C、A= D、A=1+
A、A= B、A=2+ C、A= D、A=1+ -
10. 双曲线C: (a>0,b>0)的一条渐近线的倾斜角为130°,则C的离心率为( )A、2sin40° B、2cos40° C、 D、
-
11. ∆ABC的内角A,B,C的对边分别为a,b,c,已知asinA-bsinB=4csinC,cosA= ,则 =( )A、6 B、5 C、4 D、3
-
12. 已知椭圆C的焦点为F1(-1,0),F2(1,0)。过F2的直线与C交于A,B两点。若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为( )
A、 +y2=1 B、 + =1 C、 + =1 D、 + =1
二、填空题
-
13. 曲线y=3(x2+x)ex在点(0,0)处的切线方程为.
-
14. 记Sn为等比数列{an}的前n项和。若a1= , , 则S4=
-
15. 函数f(x)=sin(2x+ )-3cosx的最小值为.
-
16. 已知 ACB=90°,P为平面ABC外一点,PC=2,点P到 ACB两边AC,BC的距离均为 ,那么P到平面ABC的距离为。
三、解答题:共70分。解答应写出文字说明,证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答。
-
17. 某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意
不满意
男顾客
40
10
女顾客
30
20
(1)、分别估计男、女顾客对该商场服务满意的概率;(2)、能否有95%的把握认为男、女顾客对该商场服务的评价有差异?附:K2=
P(K2≧k) 0.050 0.010 0.001 k 3.841 6.635 10.828 -
18. 记Sn为等差数列{an}的前n项和,已知Sn=-a5(1)、若a3=4,求{an}的通项公式。(2)、若a1≥0,求使得Sn≥an的n取值范围。
-
19. 如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2, BAD=60°,E,M,N分别是BC,BB1 , A1D的中点
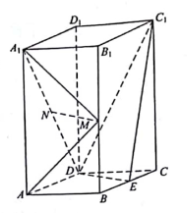 (1)、证明:MN∥平面C1DE;(2)、求点C到平面C1DE的距离。
(1)、证明:MN∥平面C1DE;(2)、求点C到平面C1DE的距离。 -
20. 已知函数f(x)=2sinx-xcosx-x,f‘(x)为f(x)的导数。(1)、证明:f'(x)在区间(0, π)存在唯一零点;(2)、若xϵ[0,π]时,f(x)≥ax,求a的取值范围。
-
21. 已知点A,B关于坐标原点O对称,|AB|=4,⊙M过点A,B且与直线x+2=0相切。(1)、若A在直线x+y=0上,求⊙M的半径。(2)、是否存在定点P,使得当A运动时,|MA|-|MP|为定值?并说明理由。
