广东省揭阳市2019届高三文数高考二模试卷

试卷更新日期：2019-06-06 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $M = {x | - 1 < x < 1}$ ， $N = {x | y = \sqrt{2 x - 1}}$ ，则 $M \cap^{} N =$ （）

A、 ${x | \frac{1}{2} \leq x < 1}$ B、 ${x | \frac{1}{2} < x < 1}$ C、 ${x | 0 \leq x < 1}$ D、 ${x | - 1 < x \leq \frac{1}{2}}$

查看试题解析
2. 复数 $\frac{i}{1 + 3 i}$ 的共轭复数的虚部为（）

A、 $\frac{1}{10}$ B、 $\frac{3}{10}$ C、 $- \frac{1}{10}$ D、 $- \frac{3}{10}$

查看试题解析
3. 已知双曲线 $m x^{2} + y^{2} = 1$ 的一条渐近线方程为 $2 x + y = 0$ ，则 $m$ 的值为（）

A、 $- \frac{1}{4}$ B、 $- 1$ C、 $- 2$ D、 $- 4$

查看试题解析

4. 通过随机询问50名性别不同的大学生是否爱好某项运动，得到如下的列联表，由

K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}

得

K^{2} = \frac{50 \times {(20 \times 15 - 10 \times 5)}^{2}}{30 \times 20 \times 25 \times 25} \approx 8.333

参照附表，得到的正确结论是（）

	爱好	不爱好	合计
男生	20	5	25
女生	10	15	25
合计	30	20	50

p（K²≥k）	0.010	0.005	0.001
k	6.635	7.879	10.828

A、有99.5％以上的把握认为“爱好该项运动与性别有关” B、有99.5％以上的把握认为“爱好该项运动与性别无关” C、在犯错误的概率不超过0.1％的前提下，认为“爱好该项运动与性别有关” D、在犯错误的概率不超过0.1％的前提下，认为“爱好该项运动与性别无关”

查看试题解析

5. 某公司2018年在各个项目中总投资500万元，下图是几类项目的投资占比情况，已知在1万元以上的项目投资中，少于3万元的项目投资占 $\frac{8}{21}$ ，那么不少于3万元的项目投资共有（）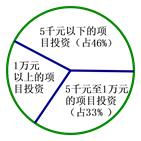

A、56万元 B、 $65$ 万元 C、 $91$ 万元 D、 $147$ 万元

查看试题解析
6. 已知 $sin θ = \frac{a - 1}{1 + a}, cos θ = - \frac{a}{1 + a}$ ，若 $θ$ 是第二象限角，则 $tan θ$ 的值为（）

A、 $- \frac{1}{2}$ B、 $- 2$ C、 $- \frac{3}{4}$ D、 $- \frac{4}{3}$

查看试题解析
7. 已知 $α ， β$ 是平面， $m ， n$ 是直线，则下列命题中不正确的是（）

A、若 $m$ ∥ $n ， m ⊥ α$ ，则 $n ⊥ α$ B、若 $m$ ∥ $α ， α \cap^{} β = n$ ，则 $m$ ∥ $n$ C、若 $m ⊥$ $α ， m ⊥ β$ ，则 $α$ ∥ $β$ D、若 $m ⊥$ $α ， m \subset β$ ，则 $α ⊥$ $β$

查看试题解析
8. 已知函数 $f (x) = {\begin{matrix} e^{- x} ， x \leq 0 ， \\ l n x ， x > 0 ， \end{matrix}$ 则 $f [f (\frac{1}{3})]$ 的是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{e}$ C、 $e$ D、 $3$

查看试题解析
9. 我国古代数学专著《九章算术》中有一个“两鼠穿墙题”，其内容为： “今有垣厚五尺，两鼠对穿，大鼠日一尺，小鼠也日一尺，大鼠日自倍，小鼠日自半。问何日相逢？各穿几何？”下图的程序框图源于这个题目，执行该程序框图，若输入 $x = 20$ ，则输出的结果为（）

A、3 B、4 C、5 D、6

查看试题解析
10. 设函数 $f (x) = cos 2 x + \sqrt{3} sin (\frac{π}{2} + 2 x)$ ，则下列结论错误的是（）

A、−2π为f(x)的一个周期 B、y=f(x)的图像关于直线x= $\frac{π}{2}$ 对称 C、f(x)的一个零点为x= $\frac{π}{4}$ D、 $f (x)$ 的最大值为2

查看试题解析
11. 设 $F$ 是椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点， $A$ 是椭圆 $E$ 的左顶点， $P$ 为直线 $x = \frac{3 a}{2}$ 上一点， $Δ A P F$ 是底角为 $30^{0}$ 的等腰三角形，则椭圆 $E$ 的离心率为（）

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
12. 若函数 $f (x)$ = $- x^{2} (x^{2} + a x + b)$ 的图像关于直线 $x = - 1$ 对称，则 $f (x)$ 的最大值是（）

A、 $- 2$ B、 $- 1$ C、0 D、1

查看试题解析

二、填空题

13. 若 $x$ ， $y$ 满足约束条件 ${\begin{matrix} x - y \geq 0 \\ x + y - 2 \leq 0 \\ y \geq 0 \end{matrix}$ ，则 $z = 3 x - 2 y$ 的最小值为.

查看试题解析
14. 已知平面向量 $\overset{⇀}{a} = (2 m + 1, - \frac{1}{2}), \overset{⇀}{b} = (2 m, 1)$ ，且 $\overset{⇀}{a}$ ∥ $\overset{⇀}{b}$ ，则实数m的值为.

查看试题解析
15. 已知四棱锥 $S - A B C D$ 的底面是边长为 $\sqrt{6}$ 的正方形，且四棱锥 $S - A B C D$ 的顶点都在半径为2的球面上，则四棱锥 $S - A B C D$ 体积的最大值为.

查看试题解析
16. 已知△ABC中， $A C = 2 \sqrt{3}$ ，D是BC边上的一点，且△ABD为等边三角形，则△ACD面积S的最大值为.

查看试题解析

三、解答题

17. 已知等差数列 ${a_{n}}$ 的前n项和为 $s_{n}$ ，公差 $d$ 不为零，若 $a_{1}, a_{3}, a_{9}$ 成等比数列，且 $S_{4} = 10$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、求证： $\frac{1}{S_{1}} + \frac{1}{S_{2}} + \dots + \frac{1}{S_{n}} < 2$ .

查看试题解析
18. 已知如图，长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = B C = 4$ ， $B B_{1} = 2 \sqrt{2}$ ，点 $E$ ， $F$ ， $M$ 分别为 $C_{1} D_{1}$ ， $A_{1} D_{1}$ ， $B_{1} C_{1}$ 的中点，过点 $M$ 的平面 $α$ 与平面 $D E F$ 平行，且与长方体的面相交，交线围成一个几何图形.

(1)、在图中画出这个几何图形，并求这个几何图形的面积（画图说出作法，不用说明理由）；

(2)、求证： $D_{1} B ⊥$ 平面 $D E F$ .

查看试题解析
19. 已知抛物线 $C ： x^{2} = 4 y$ 的焦点为F，直线 $y = k x + m (m > 0)$ 与抛物线 $C$ 交于不同的两点 $M ， N$ .

(1)、若抛物线C在点M和N处的切线互相垂直，求 $m$ 的值；

(2)、若 $m = 2$ ，求 $| M F | \cdot | N F |$ 的最小值.

查看试题解析
20. 某快递公司收取快递费用的标准是：重量不超过 $1 k g$ 的包裹收费10元；重量超过 $1 k g$ 的包裹，除收费10元之外，超过 $1 k g$ 的部分，每超出 $1 k g$ （不足 $1 k g$ ，按 $1 k g$ 计算）需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示（同一组数据用该区间的中点值作代表）.

(1)、求这60天每天包裹数量的平均值和中位数；

(2)、该公司从收取的每件快递的费用中抽取5元作为前台工作人员的工资和公司利润，剩余的作为其他费用.已知公司前台有工作人员3人，每人每天工资100元，以样本估计总体，试估计该公司每天的利润有多少元？

(3)、小明打算将 $A (0.9 k g) ， B (1.3 k g) ， C (1.8 k g) ， D (2.5 k g)$ 四件礼物随机分成两个包裹寄出，且每个包裹重量都不超过 $5 k g$ ，求他支付的快递费为45元的概率.

查看试题解析
21. 已知函数 $f (x) = x - a ln x - 1$ .

(1)、若函数 $f (x)$ 的极小值为0，求 $a$ 的值；

(2)、 $\forall t > 0$ 且 $a \leq 1$ ，求证： $f (e^{t}) > \frac{a}{2} t^{2}$ .

查看试题解析
22. 在直角坐标系 $x O y$ 中,直线 $C_{1} : y = \sqrt{3} x$ ,圆 $C_{2} : {(x - 1)}^{2} + {(y - 2)}^{2} = 5$ ,以坐标原点为极点, $x$ 轴的正半轴为极轴建立极坐标系.

(1)、求 $C_{1}, C_{2}$ 的极坐标方程;

(2)、若直线 $C_{3}$ 的极坐标方程为 $θ = \frac{π}{6} (ρ \in R)$ ,设 $C_{1}$ 与 $C_{2}$ 的交点为 $O, A,$ 圆 $C_{2}$ 与 $C_{3}$ 的交点为 $O, B$ ,求 $Δ O A B$ 的面积.

查看试题解析
23. 已知正实数x, y满足 $x + y = 1$ ．

(1)、解关于x的不等式 $| x + 2 y | + | x - y | \leq \frac{5}{2}$ ；

(2)、证明： $(\frac{1}{x^{2}} - 1) (\frac{1}{y^{2}} - 1) \geq 9$ .

查看试题解析