广东省广州市2019届高三理数第二次模拟考试试卷
试卷更新日期:2019-06-06 类型:高考模拟
一、单选题
-
1. 已知复数 在复平面内对应的点在第三象限,则实数 的取值范围是( )A、 B、 C、 D、2. 已如集合 ,则 ( )A、 或 B、 或 C、 或 D、 或3. 某公司生产 , , 三种不同型号的轿车,产量之比依次为 ,为检验该公司的产品质量,用分层抽样的方法抽取一个容量为 的样本,若样本中 种型号的轿车比 种型号的轿车少8辆,则 ( )A、96 B、72 C、48 D、364. 执行如图所示的程序框图,则输出 的值是( )
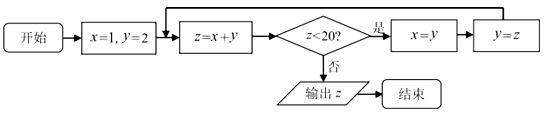 A、21 B、22 C、23 D、245. 已知点 与点 关于直线 对称,则点 的坐标为( )A、 B、 C、 D、6. 从某班6名学生(其中男生4人,女生2人)中任选3人参加学校组织的社会实践活动.设所选3人中女生人数为 ,则数学期望 ( )A、 B、1 C、 D、27. 已知 ,其中 ,则 ( )A、 B、 C、 D、8. 过双曲线 的左焦点 作圆 的切线,切点为 ,延长 交双曲线右支于点 ,若 ,则双曲线的离心率为( )A、 B、 C、 D、9. 若曲线 在点 处的切线方程为 ,且点 在直线 (其中 , )上,则 的最小值为( )A、 B、 C、 D、10. 函数 的部分图像如图所示,先把函数 图像上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的图像向右平移 个单位长度,得到函数 的图像,则函数 的图像的一条对称轴为( )
A、21 B、22 C、23 D、245. 已知点 与点 关于直线 对称,则点 的坐标为( )A、 B、 C、 D、6. 从某班6名学生(其中男生4人,女生2人)中任选3人参加学校组织的社会实践活动.设所选3人中女生人数为 ,则数学期望 ( )A、 B、1 C、 D、27. 已知 ,其中 ,则 ( )A、 B、 C、 D、8. 过双曲线 的左焦点 作圆 的切线,切点为 ,延长 交双曲线右支于点 ,若 ,则双曲线的离心率为( )A、 B、 C、 D、9. 若曲线 在点 处的切线方程为 ,且点 在直线 (其中 , )上,则 的最小值为( )A、 B、 C、 D、10. 函数 的部分图像如图所示,先把函数 图像上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的图像向右平移 个单位长度,得到函数 的图像,则函数 的图像的一条对称轴为( )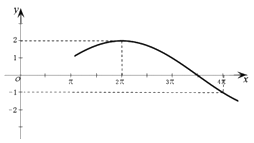 A、 B、 C、 D、11. 已知点 在直线 上,点 在直线 上, 的中点为 ,且 ,则 的取值范围为( )A、 B、 C、 D、12. 若点 与曲线 上点 的距离的最小值为 ,则实数 的值为( )A、 B、 C、 D、
A、 B、 C、 D、11. 已知点 在直线 上,点 在直线 上, 的中点为 ,且 ,则 的取值范围为( )A、 B、 C、 D、12. 若点 与曲线 上点 的距离的最小值为 ,则实数 的值为( )A、 B、 C、 D、二、填空题
-
13. 若 , 是夹角为 的两个单位向量,向量 ,则 .14. 若 的展开式中 的系数是80,则实数 的值是.15. 秦九韶是我国南宋著名数学家,在他的著作《数书九章》中有已知三边求三角形面积的方法:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”如果把以上这段文字写成公式就是 ,共中 , , 是 的内角 , , 的对边为.若 ,且 ,1, 成等差数列,则 面积 的最大值为.16. 有一个底面半径为 ,轴截面为正三角形的圆锥纸盒,在该纸盒内放一个棱长均为 的四面体,并且四面体在纸盒内可以任意转动,则 的最大值为.
三、解答题
-
17. 已知 是递增的等比数列, , .(1)、求数列 的通项公式;(2)、令 ,求数列 的前 项和 .18. 科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:
(年龄/岁)
26
27
39
41
49
53
56
58
60
61
(脂肪含量/%)
14.5
17.8
21.2
25.9
26.3
29.6
31.4
33.5
35.2
34.6
根据上表的数据得到如下的散点图.
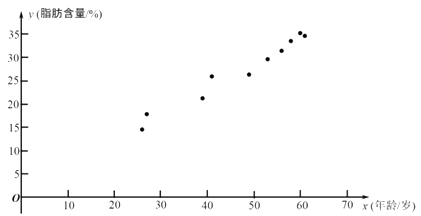 (1)、根据上表中的样本数据及其散点图:
(1)、根据上表中的样本数据及其散点图:(i)求 ;
(i)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)、若 关于 的线性回归方程为 ,求 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.附:参考数据: , , , , , ,
参考公式:相关系数
回归方程 中斜率和截距的最小二乘估计公式分别为 , .
19. 如图,在四棱锥 中,底面 为菱形, , ,且 .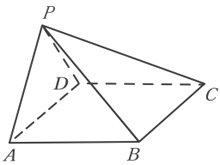 (1)、求证:平面 平面 ;(2)、若 ,求二面角 的余弦值.20. 在平面直角坐标系中,动点 分别与两个定点 , 的连线的斜率之积为 .(1)、求动点 的轨迹 的方程;(2)、设过点 的直线与轨迹 交于 , 两点,判断直线 与以线段 为直径的圆的位置关系,并说明理由.
(1)、求证:平面 平面 ;(2)、若 ,求二面角 的余弦值.20. 在平面直角坐标系中,动点 分别与两个定点 , 的连线的斜率之积为 .(1)、求动点 的轨迹 的方程;(2)、设过点 的直线与轨迹 交于 , 两点,判断直线 与以线段 为直径的圆的位置关系,并说明理由.