福建省南平市2019届普通高中毕业班理数第二次(5月)综合质量检查试卷
试卷更新日期:2019-06-06 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( ).A、 B、 C、 D、2. 若复数 满足 ,则 =( ).A、 B、 C、 D、3. 若直线 与曲线 相切于点 ,则 ( ).A、0 B、 C、 D、4. 如图,直角三角形的两直角边长分别为6和8,三角形内的空白部分是由三个半径为3的扇形构成,向该三角形内随机掷一点,则该点落在阴影部分的概率为( ).
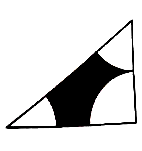 A、 B、 C、 D、5. 已知双曲线 的离心率为 ,则 的渐近线方程为( ).A、 B、 C、 D、6. 在 中,角 的对边分别是 , , , ,则 的面积为( ).A、 B、 C、 D、7. 从6位女学生和5位男学生中选出3位学生,分别担任数学、信息技术、通用技术科代表,要求这3位科代表中男、女学生都要有,则不同的选法共有( ).A、810种 B、840种 C、1620种 D、1680种8. 刘微(225-295),3世纪杰出的数学家,撞长利用切割的方法求几何体的体积,因些他定义了四种基本几何体,其中将底面是直角三角形的直三棱柱称为“堑堵”,将底面为矩形且一条侧棱垂直于底面的四棱锥称为“阳马”.已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积是( ).
A、 B、 C、 D、5. 已知双曲线 的离心率为 ,则 的渐近线方程为( ).A、 B、 C、 D、6. 在 中,角 的对边分别是 , , , ,则 的面积为( ).A、 B、 C、 D、7. 从6位女学生和5位男学生中选出3位学生,分别担任数学、信息技术、通用技术科代表,要求这3位科代表中男、女学生都要有,则不同的选法共有( ).A、810种 B、840种 C、1620种 D、1680种8. 刘微(225-295),3世纪杰出的数学家,撞长利用切割的方法求几何体的体积,因些他定义了四种基本几何体,其中将底面是直角三角形的直三棱柱称为“堑堵”,将底面为矩形且一条侧棱垂直于底面的四棱锥称为“阳马”.已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积是( ).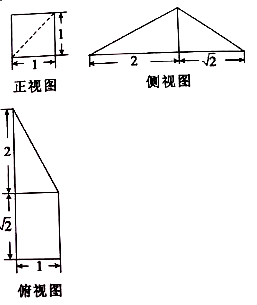 A、 B、 C、 D、9. 已知 , , ,平面区域 是由所有满足 的点 组成的区域,则区域 的面积是( ).A、8 B、12 C、16 D、2010. 已知 展开式中 的系数小于90,则 的取值范围为( ).A、 B、 C、 D、11. 在三棱锥 中, , , , ,平面 平面 ,若球 是三棱锥 的外接球,则球 的半径为( ).A、 B、 C、 D、12. 已知函数 的图像关于点 中心对称,关于直线 对称(直线 是与点 距离最近的一条对称轴),过函数 的图像上的任意一点 作点 、直线 的对称点分别为 、 ,且 ,当 时, ,记函数 的导函数为 ,则当 时, ( ).A、-2 B、-1 C、 D、
A、 B、 C、 D、9. 已知 , , ,平面区域 是由所有满足 的点 组成的区域,则区域 的面积是( ).A、8 B、12 C、16 D、2010. 已知 展开式中 的系数小于90,则 的取值范围为( ).A、 B、 C、 D、11. 在三棱锥 中, , , , ,平面 平面 ,若球 是三棱锥 的外接球,则球 的半径为( ).A、 B、 C、 D、12. 已知函数 的图像关于点 中心对称,关于直线 对称(直线 是与点 距离最近的一条对称轴),过函数 的图像上的任意一点 作点 、直线 的对称点分别为 、 ,且 ,当 时, ,记函数 的导函数为 ,则当 时, ( ).A、-2 B、-1 C、 D、二、填空题
-
13. 已知函数 在 单调递减,且为奇函数.若 ,则 的取值范围是 .14. 已知 ,则 .15. 若实数 , 满足不等式组 ,则 的最小值为 .16. 已知点 在离心率为 的椭圆 上,则该椭圆的内接八边形面积的最大值为 .
三、解答题
-
17. 已知数列 的的前 项和为 ,且1, , 成等差数列.(1)、求数列 的通项公式;(2)、数列 满足 , ,求 .18. 如图,在四棱锥 中,底面 是梯形, , , 是正三角形, 为 的中点,平面 平面 .
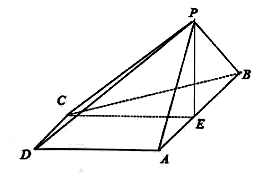 (1)、求证: 平面 ;(2)、在棱 上是否存在点 ,使得二面角 的余弦值为 ?若存在,求出 的值;若不存在,说明理由.19. 从某工厂生产的某种产品中抽取1000件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
(1)、求证: 平面 ;(2)、在棱 上是否存在点 ,使得二面角 的余弦值为 ?若存在,求出 的值;若不存在,说明理由.19. 从某工厂生产的某种产品中抽取1000件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图: (1)、求这1000件产品质量指标值的样本平均数 和样本方差 (同一组数据用该区间的中点值作代表)(2)、由频率分布直方图可以认为,这种产品的质量指标值 服从正态分布 ,其中以 近似为样本平均数 , 近似为样本方差 .
(1)、求这1000件产品质量指标值的样本平均数 和样本方差 (同一组数据用该区间的中点值作代表)(2)、由频率分布直方图可以认为,这种产品的质量指标值 服从正态分布 ,其中以 近似为样本平均数 , 近似为样本方差 .(ⅰ)利用该正态分布,求 ;
(ⅱ)某用户从该工厂购买了100件这种产品,记 表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求 .
附: .若 ,则 , .
20. 已知平面上动点 到点 距离比它到直线 距离少1.(1)、求动点 的轨迹方程;(2)、记动点 的轨迹为曲线 ,过点 作直线 与曲线 交于 两点,点 ,延长 , ,与曲线 交于 , 两点,若直线 , 的斜率分别为 , ,试探究 是否为定值?若为定值,请求出定值,若不为定值,请说明理由.