上海市黄浦区2019届高三数学二模试卷

试卷更新日期：2019-06-06 类型：高考模拟

进入出卷网下载

一、单选题

1. 设 $x \in R$ ，“ $x > 0$ ”是“ $x (x + 1) > 0$ ”的（）

A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分又非必要条件

查看试题解析
2. 已知梯形 $A B C D$ ， $A B ∥ C D$ ，设 $\overset{⇀}{A B} = \overset{⇀}{e_{1}}$ ，向量 $\overset{⇀}{e_{2}}$ 的起点和终点分别是 $A$ 、 $B$ 、 $C$ 、 $D$ 中的两个点，若对平面中任意的非零向量 $\overset{⇀}{a}$ ，都可以唯一表示为 $\overset{⇀}{e_{1}}$ 、 $\overset{⇀}{e_{2}}$ 的线性组合，那么 $\overset{⇀}{e_{2}}$ 的个数为（）

A、6 B、8 C、10 D、12

查看试题解析
3. 在某段时间内，甲地不下雨的概率为 $P_{1}$ （ $0 < P_{1} < 1$ ），乙地不下雨的概率为 $P_{2}$ （ $0 < P_{2} < 1$ ），若在这段时间内两地下雨相互独立，则这段时间内两地都下雨的概率为（）

A、 $P_{1} P_{2}$ B、 $1 - P_{1} P_{2}$ C、 $P_{1} (1 - P_{2})$ D、 $(1 - P_{1}) (1 - P_{2})$

查看试题解析
4. 在△ $A B C$ 中， $B C = a$ ， $C A = b$ ， $A B = c$ ，下列说法中正确的是（）

A、用 $\sqrt{a}$ 、 $\sqrt{b}$ 、 $\sqrt{c}$ 为边长不可以作成一个三角形 B、用 $\sqrt{a}$ 、 $\sqrt{b}$ 、 $\sqrt{c}$ 为边长一定可以作成一个锐角三角形 C、用 $\sqrt{a}$ 、 $\sqrt{b}$ 、 $\sqrt{c}$ 为边长一定可以作成一个直角三角形 D、用 $\sqrt{a}$ 、 $\sqrt{b}$ 、 $\sqrt{c}$ 为边长一定可以作成一个钝角三角形

查看试题解析

二、填空题、

5. 行列式 $| \begin{matrix} 1 \\ 4 \end{matrix} \begin{matrix} 2 \\ 7 \end{matrix} |$ 的值为．

查看试题解析
6. 计算： $lim_{n \to \infty} \frac{n^{2} - n - 2}{3 n^{2} + 1} =$ ．

查看试题解析
7. 椭圆 $\frac{x^{2}}{2} + y^{2} = 1$ 的焦距长为．

查看试题解析
8. 若函数 $f (x)$ 的反函数为 $f^{- 1} (x) = x^{\frac{1}{2}}$ ，则 $f (3) =$

查看试题解析
9. 若球主视图的面积为 $9 π$ ，则该球的体积等于

查看试题解析
10. 不等式 $\frac{1}{| x - 1 |} < \frac{1}{2}$ 的解集为

查看试题解析
11. 若等比数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n} = 3 \times 2^{n} + a$ ，则实数 $a =$

查看试题解析
12. 在 ${(\sqrt[3]{x} - \frac{2}{x})}^{n}$ 的二项展开式中，若所有项的二项式系数之和为256，则常数项等于

查看试题解析
13. 若函数 $f (x) = {\begin{matrix} x^{2} - 2 & x \leq 1 \\ lg | x - m | & x > 1 \end{matrix}$ 在区间 $[0, + \infty)$ 上单调递增，则实数 $m$ 的取值范围为

查看试题解析
14. 设 $φ \in [0, 2 π)$ ，若关于 $x$ 的方程 $sin (2 x + φ) = a$ 在区间 $[0, π]$ 上有三个解，且它们的和为 $\frac{4 π}{3}$ ，则 $φ =$

查看试题解析
15. 已知复数集合 $A = {x + y i | | x | \leq 1 ， | y | \leq 1 ， x ， y \in R}$ $B = {z_{2} | z_{2} = (\frac{3}{4} + \frac{3}{4} i) z_{1} ， z_{1} \in A}$ ，其中 $i$ 为虚数单位，若复数 $z \in A \cap^{} B$ ，则 $z$ 对应的点 $Z$ 在复平面内所形成图形的面积为

查看试题解析

三、解答题

16. 如图，在棱长为2的正方体 $A B C D - A^{'} B^{'} C^{'} D^{'}$ 中， $E$ 为 $A B$ 的中点.

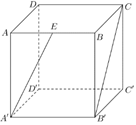(1)、求证：直线 $A^{'} E$ 平行于平面 $C C^{'} D^{'} D$ ；

(2)、求异面直线 $A^{'} E$ 与 $B^{'} C$ 所成角的大小. （结果用反三角函数值表示）

查看试题解析
17. 经济订货批量模型，是目前大多数工厂、企业等最常采用的订货方式，即某种物资在单位时间的需求量为某常数，经过某段时间后，存储量消耗下降到零，此时开始订货并随即到货，然后开始下一个存储周期，该模型适用于整批间隔进货、不允许缺货的存储问题，具体如下：年存储成本费 $T$ （元）关于每次订货 $x$ （单位）的函数关系 $T (x) = \frac{B x}{2} + \frac{A C}{x}$ ，其中 $A$ 为年需求量， $B$ 为每单位物资的年存储费， $C$ 为每次订货费. 某化工厂需用甲醇作为原料，年需求量为6000吨，每吨存储费为120元/年，每次订货费为2500元.

(1)、若该化工厂每次订购300吨甲醇，求年存储成本费；

(2)、每次需订购多少吨甲醇，可使该化工厂年存储成本费最少？最少费用为多少？

查看试题解析
18. 已知函数 $f (x) = sin x$ .

(1)、设 $a \in R$ ，判断函数 $g (x) = a \cdot f (x) + f (x + \frac{π}{2})$ 的奇偶性，并说明理由；

(2)、设函数 $F (x) = 2 f (x) - \sqrt{3}$ ，对任意 $b \in R$ ，求 $y = F (x)$ 在区间 $[b, b + 10 π]$ 上零点个数的所有可能值。

查看试题解析
19. 双曲线 $Γ : x^{2} - \frac{y^{2}}{b^{2}} = 1$ （ $b > 0$ ）.

(1)、若 $Γ$ 的一条渐近线方程为 $y = 2 x$ ，求 $Γ$ 的方程；

(2)、设 $F_{1}$ 、 $F_{2}$ 是 $Γ$ 的两个焦点， $P$ 为 $Γ$ 上一点，且 $P F_{1} ⊥ P F_{2}$ ，△ $P F_{1} F_{2}$ 的面积为9，求 $b$ 的值；

查看试题解析
20. 已知以 $a_{1}$ 为首项的数列 ${a_{n}}$ 满足： $| a_{n + 1} | = | a_{n} + 1 |$ （ $n \in N^{*}$ ）.

(1)、当 $a_{1} = - \frac{1}{3}$ 时，且 $- 1 < a_{n} < 0$ ，写出 $a_{2}$ 、 $a_{3}$ ；

(2)、若数列 ${| a_{n} |}$ （ $1 \leq n \leq 10$ ， $n \in N^{*}$ ）是公差为-1的等差数列，求a₁的取值范围；

查看试题解析