河南省平顶山市舞钢市2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2019-06-06 类型:期中考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 下列各式中,计算结果正确的是( )A、 B、 C、 D、3. 如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
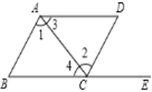 A、∠1=∠2 B、∠3=∠4 C、∠B=∠DCE D、∠D+∠DAB=180°4. 如图,描述同位角、内错角、同旁内角关系不正确的是( )
A、∠1=∠2 B、∠3=∠4 C、∠B=∠DCE D、∠D+∠DAB=180°4. 如图,描述同位角、内错角、同旁内角关系不正确的是( )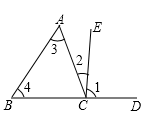 A、 与 是同位角 B、 与 是内错角 C、 与 是同旁内角 D、 与 是同旁内角5. 一蓄水池有水40立方米,按一定的速度匀速放水,水池里的水量 (立方米)与放水时间 (分钟)有如下关系:
A、 与 是同位角 B、 与 是内错角 C、 与 是同旁内角 D、 与 是同旁内角5. 一蓄水池有水40立方米,按一定的速度匀速放水,水池里的水量 (立方米)与放水时间 (分钟)有如下关系:放水时间 (分钟)
1
2
3
4
…
水池中水量 (立方米)
38
36
34
32
…
下列结论中正确的是( )
A、 随 的增加而增大 B、放水时间为15分钟时,水池中水量为8立方米 C、每分钟的放水量是2立方米 D、 与 之间的关系式为6. 如图,小轩从 处出发沿北偏东 方向行走至 处,又沿北偏西 方向行走至 处,则 的度数是( )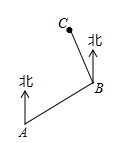 A、 B、 C、 D、7. 清明节假期的某天,小强骑车从家出发前往革命烈士陵园扫墓,匀速行驶一段时间后,因车子出现问题,途中耽搁了一段时间,车子修好后,以更快的速度匀速前行,到达烈士陵园扫完墓后匀速骑车回家.其中 表示小强从家出发后的时间, 表示小强离家的距离,下面能反映变量 与 之间关系的大致图象是( )A、
A、 B、 C、 D、7. 清明节假期的某天,小强骑车从家出发前往革命烈士陵园扫墓,匀速行驶一段时间后,因车子出现问题,途中耽搁了一段时间,车子修好后,以更快的速度匀速前行,到达烈士陵园扫完墓后匀速骑车回家.其中 表示小强从家出发后的时间, 表示小强离家的距离,下面能反映变量 与 之间关系的大致图象是( )A、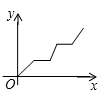 B、
B、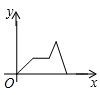 C、
C、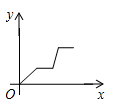 D、
D、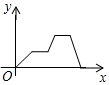 8. 如图,在边长为 的正方形中,剪去一个边长为 的小正方形( ),将余下的部分剪开后拼成一个平行四边形(如图),根据两个图形阴影部分面积的关系,可以得到一个关于 , 的恒等式为( )
8. 如图,在边长为 的正方形中,剪去一个边长为 的小正方形( ),将余下的部分剪开后拼成一个平行四边形(如图),根据两个图形阴影部分面积的关系,可以得到一个关于 , 的恒等式为( )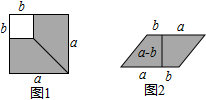 A、 B、 C、 D、9. 如图,直线 、 相交于点 , ,垂足为 ,若射线 在 的内部, , ,则 的度数为( )
A、 B、 C、 D、9. 如图,直线 、 相交于点 , ,垂足为 ,若射线 在 的内部, , ,则 的度数为( )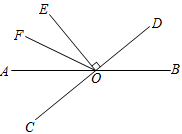 A、 B、 C、 D、10. 如图是甲、乙两车在某时段内速度随时间变化的图像,下列结论错误的是( )
A、 B、 C、 D、10. 如图是甲、乙两车在某时段内速度随时间变化的图像,下列结论错误的是( )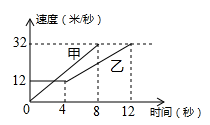 A、乙前4秒行驶的路程为48米 B、两车到第3秒时,行驶的路程相等 C、在0到8秒内甲的速度每秒增加4米 D、在4到8秒内甲的速度都大于乙的速度
A、乙前4秒行驶的路程为48米 B、两车到第3秒时,行驶的路程相等 C、在0到8秒内甲的速度每秒增加4米 D、在4到8秒内甲的速度都大于乙的速度二、填空题
-
11. 计算: .12. 若一个角的余角是其补角的 ,则这个角的度数为.13. 某游客爬山的高度 (单位: )与所用时间 (单位: )之间的关系如图所示,请根据图像提供的信息,描述游客爬山高度的变化情况:.
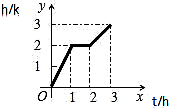 14. 若 , ,则 的值为.15. 某水库的水位在6小时内持续上涨,初始的水位高度为8米,水位以每小时0.2米的速度匀速上升,则水库的水位高度 米与时间 小时( )之间的关系式为.16. 某汽车生产厂对其生产的 型汽车进行油耗试验,试验中汽车为匀速行驶,在行使过程中,油箱的余油量 (升)与行驶时间 (小时)之间的关系如下表:
14. 若 , ,则 的值为.15. 某水库的水位在6小时内持续上涨,初始的水位高度为8米,水位以每小时0.2米的速度匀速上升,则水库的水位高度 米与时间 小时( )之间的关系式为.16. 某汽车生产厂对其生产的 型汽车进行油耗试验,试验中汽车为匀速行驶,在行使过程中,油箱的余油量 (升)与行驶时间 (小时)之间的关系如下表:(小时)
0
1
2
3
(升)
100
92
84
76
由表格中 与 的关系可知,当汽车行驶小时,油箱的余油量为40升.
17. 将一张长方形纸片 沿 折叠,顶点 , 分别落在点 , 处,且 交 于 , ,则 .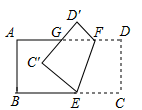 18. 按一定规律排列的一列数: , , , , , ,…,若 、 、 表示这列数中依次排列的连续的三个数,猜想 、 、 满足的关系式是.
18. 按一定规律排列的一列数: , , , , , ,…,若 、 、 表示这列数中依次排列的连续的三个数,猜想 、 、 满足的关系式是.三、解答题
-
19.(1)、(2)、20. 先化简,再求值: ,其中 , .21. 如图所示,已知 , 平分 , 与 相交于点 , ,试说明 .
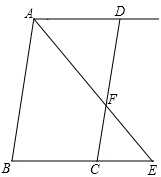 22. 下表是橘子的销售额随橘子卖出质量的变化表:
22. 下表是橘子的销售额随橘子卖出质量的变化表:质量/千克
1
2
3
4
5
6
7
8
9
…
销售额/元
2
4
6
8
10
12
14
16
18
…
(1)、这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、当橘子卖出5千克时,销售额是元.(3)、如果用 表示橘子卖出的质量, 表示销售额,按表中给出的关系, 与 之间的关系式为.(4)、当橘子的销售额是100元时,共卖出多少千克橘子?23. 作图题:如图,点 , 均在直线 上, . (1)、在图中作 ,使 (保留作图痕迹,不写作法).(2)、请直接说出直线 与直线 的位置关系.24. 小明家距离学校8千米,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他以更快的速度匀速骑车到校。我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行驶的路程(千米)与他所用的时间(分钟)之间的关系。请根据图象,解答下列问题:
(1)、在图中作 ,使 (保留作图痕迹,不写作法).(2)、请直接说出直线 与直线 的位置关系.24. 小明家距离学校8千米,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他以更快的速度匀速骑车到校。我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行驶的路程(千米)与他所用的时间(分钟)之间的关系。请根据图象,解答下列问题: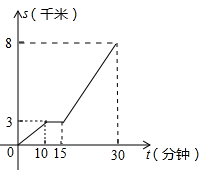 (1)、小明行了多少千米时,自行车出现故障?修车用了几分钟?(2)、小明从早晨出发直到到达学校共用了多少分钟?(3)、小明修车前、后的行驶速度分别是多少?(4)、如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟?25. 已知:如图所示,直线 ,另一直线交 于 ,交 于 ,且 ,点 为直线 上一动点,过点 的直线交 于点 ,且 .
(1)、小明行了多少千米时,自行车出现故障?修车用了几分钟?(2)、小明从早晨出发直到到达学校共用了多少分钟?(3)、小明修车前、后的行驶速度分别是多少?(4)、如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟?25. 已知:如图所示,直线 ,另一直线交 于 ,交 于 ,且 ,点 为直线 上一动点,过点 的直线交 于点 ,且 .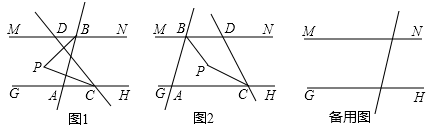 (1)、如图1,当点 在点 右边且点 在点 左边时, 的平分线与 的平分线交于点 ,求 的度数;(2)、如图2,当点 在点 右边且点 在点 右边时, 的平分线与 的平分线交于点 ,求 的度数;(3)、当点 在点 左边且点 在点 左边时, 的平分线与 的平分线所在直线交于点 ,请直接写出 的度数,不说明理由.
(1)、如图1,当点 在点 右边且点 在点 左边时, 的平分线与 的平分线交于点 ,求 的度数;(2)、如图2,当点 在点 右边且点 在点 右边时, 的平分线与 的平分线交于点 ,求 的度数;(3)、当点 在点 左边且点 在点 左边时, 的平分线与 的平分线所在直线交于点 ,请直接写出 的度数,不说明理由.