广西玉林市玉州区2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期：2019-06-06 类型：期中考试
一、单选题
-
1. 的相反数是（ ）A、 B、 C、 D、 +12. 下列图形中，不能通过其中一个四边形平移得到的是（ ）A、
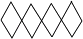B、
C、
D、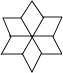
3. 实数9的算术平方根为（ ）A、 B、 C、3 D、±34. 下列实数是无理数的是（ ）A、3.14159 B、 C、 D、5. 在平面直角坐标系xOy中，若点P在第四象限，且点P到x轴的距离为1，到y轴的距离为3，则点的坐标为（ ）A、(3,-1) B、(-3,1) C、(1,-3) D、(-1,3)6. 如图，在数轴上的几点中与表示 的点最接近的点是（ ）
A、点A B、点B C、点C D、点D7. 如图，点A表示的数为-1，直径为1个单位长度的圆从A点沿数轴向右滚动(无滑动)两周到达点B，则点B表示的数是（ ）
A、π B、2π C、2π-1 D、2π+18. 请你观察、思考下列计算过程：因为112=121，所以 =11：，因为1112=12321所以 =111…，由此猜想 =（ ）A、111111 B、1111111 C、11111111 D、1111111119. 有下列命题：(1)无理数就是开方开不尽的数；(2)无理数包括正无理数、零、负无理数；(3)在同一平面内，垂直于同一直线的两直线平行；(4)在同一平面内，过一点有且只有一条直线与已知直线垂直。其中假命题的个数是（ ）A、1 B、2 C、3 D、410. 点A(-3，-5)向右平移2个单位，再向下平移3个单位到点B，则点B的坐标为（ ）A、(-5,-8) B、(-5,-2) C、(-1,-8) D、(-1,-2)11. 如图，AB∥EF，∠C=90°，则a、B、y的关系是（ ）
A、β+γ-α=90° B、α+β-γ=90° C、α+β+γ=180° D、β=α+γ12. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)，…按这样的运动规律，经过第2019次运动后，动点P的坐标是（ ）
A、（2018，0） B、（2018，1） C、（2019，1） D、（2019，2）二、填空题
-
13. 写出一个在x轴正半轴上的点坐标14. 若一个数的立方根等于这个数的算术平方根，则这个数是.15. 把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45角)如图放置，使直角顶点C重合，若DE∥BC，则∠1的度数是
16. 下列命题中：①若 ，则 ；②两直线平行，同位角相等；③对顶角相等；④内错角相等，两直线平行.是真命题的是.（填写所有真命题的序号）
17. 为了求1+2+22+23+…+22016的值，可令S=1+2+22+…+22016 ， 则2S=2+22+23+24+…+22017 ， 因此2S–S=22017-1，所以1+2+22+23+…+22016=22017-1。仿照以上推理计算出1+5+52+53+…+52019的值是18. 若 的整数部分为a，小数部分为b，求a2+b- 的值为三、解答题
-
19. 计算: - +|1- .20. 将下列各数填入相应的集合内-7,0.32, ,0, , , , ,0.1010010001….
①有理数集合{ … }
②无理数集合{ … }
③负实数集合{ … }.
21. 求式中的x的值:25(x-1)2=49；22. 在平面直角坐标系中，A，B，C三点的坐标分别为（-6，7）、（-3，0）、（0，3）.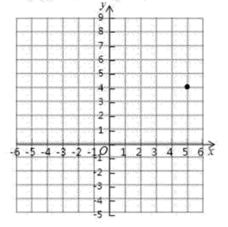
(1)、画出△ABC，并求△ABC的面积.(2)、在平面直角坐标系中平移△ABC，使点C经过平移后的对应点为C'(5，4)，平移后△ABC得到△A'B'C'，画出平移后的△A'B'C'，并写出点A'，B'的坐标(3)、P(-3，m)为△ABC中一点，将点P向右平移4个单位后，再向上平移6个单位得到点Q(n，-3)，则m=n=23. 完成下面的证明过程：如图所示，
直线AD与AB，CD分别相交于点A，D，与EC，BF分别相交于点H，G，已知∠1＝∠2，∠B＝∠C.
求证：∠A＝∠D.
证明：∵∠1＝∠2，（已知）∠2＝∠AGB（）
∴∠1＝
∴EC∥BF（）
∴∠B＝∠AEC（）
又∵∠B＝∠C（已知）
∴∠AEC＝（）
∴（）
∴∠A＝∠D（）
24. 已知a+2是1的平方根,3是b-3的立方根， 的整数部分为c，求a+b+c的值25. 如图所示，A(2，0)、点B在y轴上，将三角形OAB沿x轴负方向平移，平移后的图形为三角形DEC，且点C的坐标为(a，b)，且a= + -6
(1)、求点C的坐标；(2)、求点E的坐标；(3)、点P是CE上一动点，设∠CBP=x°，∠PAD=y°，∠BPA=z°，确定x，y，z之间的数量c关系，并证明你的结论26. 如图1，在平面直角坐标系中，A(a，0)，C(b，4)，且满足(a+4)2+ =0，过C作CB⊥x轴于B。
(1)、求三角形ABC的面积；(2)、如图2，若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，求∠AED的度数；(3)、在y轴上是否存在点P，使得三角形ACP和三角形ABC的面积相等?若存在，求出P点的坐标；若不存在，请说明理由