广西贵港市港南区2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2019-06-06 类型：期中考试

进入出卷网下载

一、单选题

1. 化简 $(- 3 x^{2}) \cdot 2 x^{3}$ 的结果是（）

A、 $- 6 x^{5}$ B、 $- 3 x^{5}$ C、 $2 x^{5}$ D、 $6 x^{5}$

查看试题解析
2. 下列是二元一次方程的是（）

A、3x-6=x B、3x=2y C、x- $y^{2}$ =0 D、2x-3y=xy

查看试题解析
3. 多项式 $m x^{2} - m$ 与多项式 $x^{2} - 2 x + 1$ 的公因式是（）

A、 $x - 1$ B、 $x + 1$ C、 $x^{2} - 1$ D、 ${(x - 1)}^{2}$

查看试题解析
4. 把代数式ax²-4ax+4a因式分解，下列结果中正确的是（）

A、a(x-2)² B、a(x+2)² C、a(x-4)² D、a(x+2)(x-2)

查看试题解析
5. 如果 $x^{2} - (m + 1) x + 1$ 是完全平方式，则m的值为（）

A、-1 B、1 C、1或-1 D、1或-3

查看试题解析
6. 下列从左边到右边的变形，是因式分解的是（）

A、 $(3 - x) (3 + x) = 9 - x^{2}$ B、 $(y + 1) (y - 3) = - (3 - y) (y + 1)$ C、 $4 y z - 2 y^{2} z + z = 2 y (2 z - y z) + z$ D、 $- 8 x^{2} + 8 x - 2 = - 2 {(2 x - 1)}^{2}$

查看试题解析
7. 已知方程组 ${\begin{matrix} 2 x + y = 4 \\ x + 2 y = 5 \end{matrix}$ ，则 $x + y$ 的值为（）

A、 $- 1$ B、0 C、2 D、3

查看试题解析
8. 规用190张铁皮做盒子，每张铁皮做8个盒身或做22个盒底，而一个盒身与两个盒底配成一个盒子，设用x张铁皮做盒身，y张铁皮做盒底，则可列方程组为（）

A、 ${\begin{matrix} x + y = 190 \\ 2 \times 8 x = 22 y \end{matrix}$ B、 ${\begin{matrix} x + y = 190 \\ 2 \times 22 y = 8 x \end{matrix}$ C、 ${\begin{matrix} 2 x + y = 190 \\ 8 x = 22 y \end{matrix}$ D、 ${\begin{matrix} x + 2 y = 190 \\ 2 \times 8 x = 22 y \end{matrix}$

查看试题解析
9. 计算：(a－b)(a＋b)(a²＋b²)(a⁴+b⁴)的结果是（）

A、a⁸＋2a⁴b⁴＋b⁸ B、a⁸－2a⁴b⁴＋b⁸ C、a⁸＋b⁸ D、a⁸－b⁸

查看试题解析
10. 将图(甲)中阴影部分的小长方形变换到图(乙)位置，根据两个图形的面积关系得到的数学公式是（）

A、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 $a^{2} - b^{2} = (a + b) (a - b)$ D、 $(a + 2 b) (a - b) = a^{2} + a b - 2 b^{2}$

查看试题解析
11. 如图，边长为a，b的矩形的周长为14，面积为10，则a²b+ab²的值为（）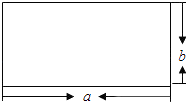

A、140 B、70 C、35 D、24

查看试题解析
12. 在求 $1 + 6 + 6^{2} + 6^{3} + 6^{4} + 6^{5} + 6^{6} + 6^{7} + 6^{8} + 6^{9}$ 的值时，小林发现：从第二个加数起每一个加数都是前一个加数的6倍，于是她设： $S = 1 + 6 + 6^{2} + 6^{3} + 6^{4} + 6^{5} + 6^{6} + 6^{7} + 6^{8} + 6^{9}$ ……①
然后在①式的两边都乘以6，得： $6 S = 6 + 6^{2} + 6^{3} + 6^{4} + 6^{5} + 6^{6} + 6^{7} + 6^{8} + 6^{9} + 6^{10}$ ……②

②-①得 $6 S - S = 6^{10} - 1$ ，即 $5 S = 6^{10} - 1$ ，所以 $S = \frac{6^{10} - 1}{5}$ .

得出答案后，爱动脑筋的小林想：如果把“6”换成字母“a”(a≠0且a≠1)，能否求出 $1 + a + a^{2} + a^{3} + a^{4} + ... + a^{2018}$ 的值?你的答案是（）

A、 $\frac{a^{2018} - 1}{a - 1}$ B、 $\frac{a^{2019} - 1}{a - 1}$ C、 $\frac{a^{2018} - 1}{a}$ D、 $a^{2019} - 1$

查看试题解析

二、填空题

13. 计算： ${(- 3)}^{2019} \cdot {(- \frac{1}{3})}^{2017}$ =.

查看试题解析
14. 分解因式： $4 a^{4} - 16 a^{2} =$ .

查看试题解析
15. 若方程 $4 x^{m - n} - 5 y^{m + n} = 6$ 是二元一次方程，则m= ， n=.

查看试题解析
16. 已知 $x + \frac{1}{x} = 2$ ，则 $x^{2} + \frac{1}{x^{2}} =$ .

查看试题解析
17. 若 ${\begin{cases} x = a \\ y = b \end{cases}$ 是方程2x+y=0的解，则6a+3b+2= ．

查看试题解析
18. 有甲，乙，丙三种笔，已知买甲种笔2支和乙种1支，丙种3支共12.5元，买甲种笔1支，乙种，4支，丙种5支，共18.5元，那么买甲种笔1支和乙种2支，丙种3支共需元.

查看试题解析

三、解答题

19. 把下列多项式因式分解：

(1)、 $x^{2} - 9$

(2)、 $4 x^{2} - 3 y (4 x - 3 y)$

查看试题解析
20. 先化简，再求值：3a(2a²－4a＋3)－2a²(3a＋4)，其中a＝－2.

查看试题解析
21. 若x+y=3，且(x+2)(y+2)=12.

(1)、求xy的值；

(2)、求x²+3xy+y²的值.

查看试题解析
22. 解二元一次方程组：

(1)、 ${\begin{matrix} 2 x - y = - 2 \\ x + y = 5 \end{matrix}$

(2)、 ${\begin{matrix} x + 4 y = 14 \\ \frac{x - 3}{4} + \frac{y - 3}{3} = \frac{1}{12} \end{matrix}$

查看试题解析
23. 长方形地砖排成一个长方形，每块长方形地砖的长和宽分别是多少?

查看试题解析
24.

(1)、已知 $a^{x} = 5$ ， $a^{x + y} = 5$ ，求 $a^{x} + a^{y}$ 的值；

(2)、已知 $10^{α} = 5$ ， $10^{β} = 6$ ，求 $10^{2 α + 2 β}$ 的值.

查看试题解析
25. 阅读材料：小明在解方程组 ${\begin{matrix} 2 x + 5 y = 3...... ① \\ 4 x + 11 y = 5..... ② \end{matrix}$ 时，采用了一种“整体代换”解法：
解：将方程②变形：4x+10y+y=5即2(2x+5y)+y=5......③

把方程①代入③得：2×3+y=5，

y=-1

y=-1代入①得x=4

∴方程组的解为 ${\begin{matrix} x = 4 \\ y = - 1 \end{matrix}$

请你解决以下问题：

(1)、参考小明的“整体代换”法解方程组 ${\begin{matrix} 3 x - 2 y = 5....... ① \\ 4 x - 4 y = 19..... ② \end{matrix}$

(2)、已知x，y满足方程组： ${\begin{matrix} 3 x^{2} - 2 x y + 12 y^{2} = 47....... ① \\ 2 x^{2} + x y + 8 y^{2} = 36........... ② \end{matrix}$
(i)求 $x^{2} + 4 y^{2}$ 的值；

(ii)求 $\frac{1}{x} + \frac{1}{2 y}$ 的值.

查看试题解析
26. 一家商店进行装修，若请甲、乙两个装修组同时施工，8天可以完成，需付两组费用共3520元，若先请甲组单独做6天，再请乙组单独做12天可以完成，需付费用3480元，问：

(1)、甲，乙两组工作一天，商店各应付多少钱?

(2)、已知甲单独完成需12天，乙单独完成需24天，单独请哪个组，商店所需费用最少?

(3)、若装修完后，商店每天可赢利200元，你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)

查看试题解析