浙江省慈溪市2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2019-06-06 类型:期中考试
一、单选题
-
1. 下列所给图形既是中心对称图形又是轴对称图形的是( )A、
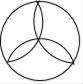 B、
B、 C、
C、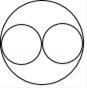 D、
D、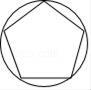 2. 若式子 有意义,则x的取值范围是( )A、 B、 C、 D、3. 下列方程中,是关于x的一元二次方程的是( )A、 B、 C、 D、4. 甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩都为9环,方差分别为S甲2=0.56,S乙2=0.62,S丙2=0.39,S丁2=0.42,则四人中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁5. 如图,在▱ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( )
2. 若式子 有意义,则x的取值范围是( )A、 B、 C、 D、3. 下列方程中,是关于x的一元二次方程的是( )A、 B、 C、 D、4. 甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩都为9环,方差分别为S甲2=0.56,S乙2=0.62,S丙2=0.39,S丁2=0.42,则四人中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁5. 如图,在▱ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( ) A、100° B、95° C、90° D、85°6. 用配方法解方程 时,应将其变形为( )A、 B、 C、 D、7. 某商场对上周女装的销售情况进行了统计,销售情况如表:
A、100° B、95° C、90° D、85°6. 用配方法解方程 时,应将其变形为( )A、 B、 C、 D、7. 某商场对上周女装的销售情况进行了统计,销售情况如表:颜色
黄色
绿色
白色
紫色
红色
数量(件)
100
180
220
80
550
经理决定本周进女装时多进一些红色的,可用来解释这一现象的统计知识是( )
A、平均数 B、中位数 C、众数 D、方差8. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是 ,设金色纸边的宽为xcm,那么x满足的方程是 A、 B、 C、 D、9. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°, ,则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ,正确的个数是( )
A、 B、 C、 D、9. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°, ,则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ,正确的个数是( ) A、1 B、2 C、3 D、410. 如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最大值与最小值的差为( )
A、1 B、2 C、3 D、410. 如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最大值与最小值的差为( ) A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
11. 计算:(1)、 = ,(2)、( )2= ,(3)、 ﹣9 = ,(4)、 (2 ﹣ )= .12. 一元二次方程y2=2y的解为 .13. 若正 边形的每个内角都等于150°,则 的值为 .14. 某组数据按从小到大的顺序如下:2、4、8、x、10、14,已知这组数据的中位数是9,则这组数据的众数是.15.
如图,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是 (只填写一个条件,不使用图形以外的字母和线段).
 16. 如图,直线AB、CD被直线EF所截,∠1、∠2是同位角,如果∠1≠∠2,那么AB与CD不平行.用反证法证明这个命题时,应先假设:.
16. 如图,直线AB、CD被直线EF所截,∠1、∠2是同位角,如果∠1≠∠2,那么AB与CD不平行.用反证法证明这个命题时,应先假设:.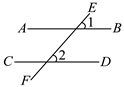 17. 已知x为实数,且满足 ,那么x2+3x=.
17. 已知x为实数,且满足 ,那么x2+3x=.
18. 如图,小明用三个等腰三角形(图中①②③)拼成了一个平行四边形ABCD,且 ,则 = 度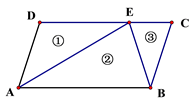
三、解答题
-
19. 计算:(1)、(2)、20. 用适当方法解下列方程:(1)、 ;(2)、 .21. 某校为了解全校1600名学生每周课外体育活动时间的情况,随机调查了其中的部分学生,对这些学生每周课外体育活动时间x(单位:小时)进行了统计,根据所得数据绘制了一幅统计图,根据以上信息及统计图解答下列问题
 (1)、本次接受随机抽样调查的学生人数为;(2)、求这些学生每周课外体育活动时间的平均数;(3)、估计全校学生每周课外体育活动时间不少于4小时的人数 .22. 已知关于x的方程 =0.
(1)、本次接受随机抽样调查的学生人数为;(2)、求这些学生每周课外体育活动时间的平均数;(3)、估计全校学生每周课外体育活动时间不少于4小时的人数 .22. 已知关于x的方程 =0.
(1)、求证:不论a取何实数,该方程都有两个不相等的实数根。(2)、当a=1时,求该方程的根。
