云南省保山市2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2019-06-06 类型：期中考试

进入出卷网下载

一、单选题

1. 下列根式中，不是最简二次根式的是（）

A、 $\sqrt{18}$ B、 $\sqrt{10}$ C、 $\sqrt{6}$ D、 $\sqrt{2}$

查看试题解析
2. 下列各组数中，能构成直角三角形的是（）

A、4，5，6 B、1，1， $\sqrt{2}$ C、6，8，11 D、5，12，23

查看试题解析
3. 下列计算正确的是（）

A、 $2 \sqrt{3} \times 3 \sqrt{3} = 6 \sqrt{3}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\sqrt{2} \div \sqrt{3} = \frac{\sqrt{6}}{3}$ D、 $5 \sqrt{5} - 2 \sqrt{2} = 3 \sqrt{3}$

查看试题解析
4. 平行四边形具有的性质是（）

A、四边相等 B、对角线相等 C、对角线互相平分 D、四个角都是直角

查看试题解析
5. 如图，字母B所代表的正方形的面积是（）

A、12cm² B、15cm² C、306cm² D、144cm²

查看试题解析
6. 如图，在▱ABCD中，已知AD=12cm，AB=8cm，AE平分∠BAD交BC边于点E，则CE的长等于（　）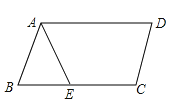　

A、8cm B、6cm C、4cm D、2cm

查看试题解析
7. 如图，在长方形ABCD中无重叠放入面积分别为16cm²和12cm²的两张正方形纸片，则图中空白部分的面积为（）cm².

A、16﹣8 $\sqrt{3}$ B、﹣12+8 $\sqrt{3}$ C、8﹣4 $\sqrt{3}$ D、4﹣2 $\sqrt{3}$

查看试题解析
8. 已知如图，折叠长方形的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm，则EC=（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

9. 比较大小： $2 \sqrt{3}$ $3 \sqrt{2}$ ．（填“＞、＜、或=”）

查看试题解析
10. 式子 $\sqrt{x - 3}$ 在实数范围内有意义，则 x 的取值范围是．

查看试题解析
11. 如图，已知AD∥BC，要使四边形 ABCD 为平行四边形，需要添加的一个条件是：.(填一个你认为正确的条件即可，不再添加任何线段与字母)

查看试题解析
12. 在平行四边形ABCD中，∠B+∠D=180 $°$ ，则∠A=.

查看试题解析
13. 已知三角形三边长为a，b，c，如果 $\sqrt{a - 6}$ +|b﹣8|+(c﹣10)²=0，则△ABC是三角形.

查看试题解析
14. 如图，平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点B的坐标为(10，6)，点P为BC边上的动点，当△POA为等腰三角形时，点P的坐标为.

查看试题解析

三、解答题

15. 计算

(1)、 $2 \sqrt{3} + \sqrt{8} - \sqrt{2} - \sqrt{27}$

(2)、 ${(\sqrt{2} - \sqrt{3})}^{2} + 2 \sqrt{\frac{1}{3}} \times 3 \sqrt{2}$

查看试题解析
16. 如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点.

(1)、在图①中，以格点为端点，画线段MN= $\sqrt{13}$ ；

(2)、在图②中，以格点为顶点，画正方形ABCD，使它的面积为10.

查看试题解析
17. 如图，在四边形ABCD中，∠B＝90º，AB=BC=2，AD＝1，CD＝3.求∠DAB的度数.

查看试题解析
18. 如图所示，在▱ABCD中，AE⊥BD，CF⊥BD，垂足分别为E，F，求证：BE=DF.

查看试题解析
19. 在▱ABCD中AB=6，BC=8，AC=10.

(1)、求证：四边形ABCD是矩形；

(2)、求BD的长.

查看试题解析
20. 甲、乙两船同时从港口A出发，甲船以12海里/时的速度向北偏东35°航行，乙船向南偏东55°航行.2小时后，甲船到达C岛，乙船到达B岛，若C、B两船相距40海里，问乙船的速度是每小时多少海里？

查看试题解析
21. 如图，梯形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于点E.求证：四边形AECD是菱形.

查看试题解析
22. 小东拿着一根长竹竿进一个宽为3米的门，他先横着拿，进不去，又竖起来拿，结果竿比门高1米，当他把竿斜着时，两端刚好顶着门的对角，问：竹竿高多少米？

查看试题解析
23. 四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM.

(1)、求证：AM=AD+MC.

(2)、若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，试判断AM=AD+MC是否成立？若成立，请给出证明，若不成立，请说明理由；

查看试题解析