湖北省鄂州市梁子湖区2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2019-06-06 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算中，正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ C、 $2 \sqrt{3} - \sqrt{3} = 2$ D、 $\sqrt{\frac{1}{2}} = 2 \sqrt{2}$

查看试题解析
2. 要使二次根式 $\sqrt{x - 3}$ 在实数范围内有意义，则x的取值范围是（）

A、x≠3 B、x≤3 C、x＞3 D、x≥3

查看试题解析
3. △ABC的三边长分别为a，b，c，下列条件：①∠A=∠B-∠C；②∠A：∠B：∠C=3：4：5；③a²=（b+c）（b-c）；④a：b：c=5：12：13，其中能判断△ABC是直角三角形的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如图，在Rt△AED中，∠E＝90°，AE＝3，ED＝4，以AD为边在△AED的外侧作正方形ABCD，则正方形ABCD的面积是（）

A、5 B、25 C、7 D、10

查看试题解析
5. 下列条件中，能判定四边形ABCD为平行四边形的个数是（）
①AB∥CD，AD＝BC ②AB＝CD，AD＝BC；③∠A＝∠B，∠C＝∠D；④AB＝AD，CB＝CD.

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，一架长5米的梯子AB，斜靠在一竖直的墙上，这时梯子底端距墙底3米，若梯子的顶端沿墙下滑1米，则梯子的底端在水平方向上将滑动（）

A、0米 B、1米 C、2米 D、3米

查看试题解析
7. 若1≤a≤ $\sqrt{2}$ ，则化简 $\sqrt{a^{2} - 2 a + 1} + | a - 2 |$ 的结果是（）

A、 $6 + a$ B、 $- 6 - a$ C、 $- a$ D、1

查看试题解析
8. 如图，平面直角坐标系中，点O，B，D的坐标分别是（0，0），（5，0），（2，3），若存在点C，使得以点O，B，D，C为顶点的四边形是平行四边形，则下列给出的点C的坐标中，错误的是（）

A、（3，－3） B、（－3，3） C、（3，5） D、（7，3）

查看试题解析
9. 如图，在平行四边形ABCD中，对角线AC，BD相交于点O，若BD，AC的和，为18cm，CD：DA=2：3，△AOB的周长为13cm，那么BC的长是（）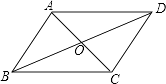

A、6cm B、9cm C、3cm D、12cm

查看试题解析
10. 如图，△ABC中，∠BAC＝60°，∠B＝45°，AB＝2，点D是BC上的一个动点，点D关于AB，AC的对称点分别是点E，F，四边形AEGF是平行四边形，则四边形AEGF面积的最小值是（）

A、1 B、 $\frac{\sqrt{6}}{2}$ C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析

二、填空题

11. 化简 $\sqrt{12} =$ ．

查看试题解析
12. 如图，数轴上点A表示数－1，点B表示数1，过点B作BC垂直于数轴，若BC＝1，以A为圆心，AC为半径作圆弧交数轴的正半轴于点P，则点P所表示的数是 .

查看试题解析
13. 如图，已知长方体的长、宽、高分别为4 cm，3 cm，12 cm，在其中放入一根细棒，则细棒的最大长度可以是 cm.

查看试题解析
14. 如图，在平行四边形ABCD中，DB＝DC，∠C＝70°，AE⊥BD于E，则∠DAE＝度.

查看试题解析
15. 如图，直线l₁ ， l₂ ， l₃分别过正方形ABCD的三个顶点A，D，C，且相互平行，若l₁ ， l₂的距离为2，l₂ ， l₃的距离为4，则正方形的对角线长为.

查看试题解析
16. 如图，△ABC中，∠ABC＝45°，∠BCA＝30°，点D在BC上，点E在△ABC外，且AD＝AE＝CE，AD⊥AE，则 $\frac{A B}{B D}$ 的值为.

查看试题解析

三、解答题

17. 计算:

(1)、 $\sqrt{8} + \sqrt{\frac{1}{3}} - \sqrt{\frac{1}{2}} + \frac{\sqrt{3}}{2}$ ；

(2)、 $(3 \sqrt{12} - 2 \sqrt{\frac{1}{3}} + \sqrt{48})$ $\div 2 \sqrt{3}$ .

查看试题解析
18. 如图，在平行四边形ABCD中，点E、F在AC上，且AF＝CE，点G、H分别在AB、CD上，且AG＝CH，AC与GH相交于点O.

(1)、求证：EG//FH；

(2)、GH、EF互相平分.

查看试题解析
19. 如图，在四边形ABCD中，AB＝BC＝CD＝AD＝4，∠DAB＝∠B＝∠C＝∠D＝90°，E，F分别是边BC，CD上的点，且CE＝ $\frac{1}{4}$ BC，F为CD的中点，问△AEF是什么三角形？请说明理由.

查看试题解析
20. 已知m＝ $\sqrt{7}$ ＋2，n＝ $\sqrt{7}$ －2，求下列各式的值：

(1)、（m＋1）(n＋1)；

(2)、 $\frac{m}{n} + \frac{n}{m}$ .

查看试题解析
21. 如图，在四边形ABCD中，∠A＝∠ABC＝90°，AD＝1，BC＝3，点E是边CD的中点，连接BE并延长交AD的延长线于点F，连接CF.

(1)、求证：四边形BDFC是平行四边形；

(2)、若CB＝CD，求四边形BDFC的面积.

查看试题解析
22. 如图，在△ABC中，点E是边AC上一点，线段BE垂直于∠BAC的平分线于点D，点M为边BC的中点，连接DM.

(1)、求证： DM＝ $\frac{1}{2}$ CE；

(2)、若AD＝6，BD＝8，DM＝2，求AC的长.

查看试题解析
23. 如图，已知△ABC中，∠B=90°，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．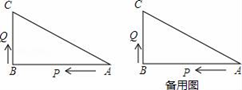

(1)、出发2秒后，求PQ的长；

(2)、当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？

(3)、当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

查看试题解析
24. 如图，在平面直角坐标系中，已知A（0，5）， B（a，b），且a，b满足b＝ $\sqrt{a - 4}$ ＋ $\sqrt{4 - a}$ －1.

(1)、如图，求线段AB的长；

(2)、如图，直线CD与x轴、y轴正半轴分别交于点C，D，∠OCD＝45°，第四象限的点P（m，n）在直线CD上，且mn＝－6，求OP²－OC²的值；

(3)、如图，若点D（1，0），求∠DAO ＋∠BAO的度数.

查看试题解析