广西贵港市港南区2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期：2019-06-06 类型：期中考试
一、单选题
-
1. 具备下列条件的△ABC中，不是直角三角形的是（ ）A、∠A＋∠B=∠C B、∠A－∠B=∠C C、∠A︰∠B︰∠C =1︰2︰3 D、∠A=∠B=3∠C2. 点P在∠A0B的平分线上，点P到OA边的距离等于5，点Q是0B边上的任意一点，则下列不符合题意的是（ ）A、PQ≤5 B、PQ<5 C、PQ≥5 D、PQ>53. 已知一个多边形的内角和等于900º，则这个多边形是（ ）A、五边形 B、六边形 C、七边形 D、八边形4. 已知AD是△ABC的中线，且△ABD比△ACD的周长大3cm，则AB与AC的差为（ ）A、2cm B、3cm C、4cm D、6cm5. 三角形一边上的中线把原三角形一定分成两个（ ）A、形状相同的三角形 B、面积相等的三角形 C、直角三角形 D、周长相等的三角形6. 如图，在 中，CD是斜边AB上的中线，若 ，则 的度数为
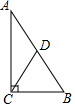A、 B、 C、 D、7. 如图，已知△ABC中，∠C=90°，AD平分∠BAC，且CD：BD=3：4.若BC=21，则点D到AB边的距离为（ ）
A、7 B、9 C、11 D、148. 如图，在ΔABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E，若AB=6cm，则ΔDBE的周长是（ ）
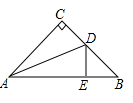A、6cm B、7cm C、8cm D、9 cm9.如图，在正方形ABCD的外侧，作等边三角形ADE，AC、BE相交于点F，则∠BFC为（ ）
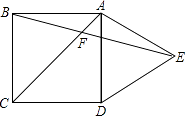A、45° B、55° C、60° D、75°10. 如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于点H，则DH等于（ ）
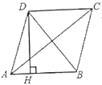A、 B、 C、5 D、4511. 如图，P是矩形ABCD的对角线AC的中点，E是AD的中点．若AB=6，AD=8，则四边形ABPE的周长为（ ）
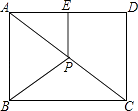A、14 B、16 C、17 D、18二、填空题
-
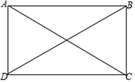
12. 正六边形的每个内角等于°．13. 矩形是中心对称图形，对矩形ABCD而言，点A的对称点是点.
14. 如图所示，点O是直线AB上的点，OC平分∠AOD，∠BOD=40°，则∠AOC=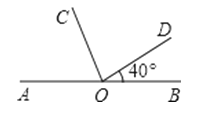
15. 如图，在△ABC中，CD平分∠ACB交AB于点D，DE⊥AC交于点E，DF⊥BC于点F，且BC=4，DE=2，则△BCD的面积是 ．
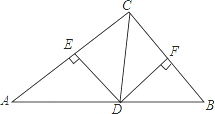16. 如图，在△ABC中，∠C＝90°，∠B＝30°，AD平分∠CAB，交BC于点D，若CD＝1，则BD＝ ．
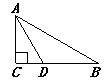17. 如图，在四边形ABCD中，∠ADC＝∠ABC＝90°，AD＝CD，DP⊥AB于P.若四边形ABCD的面积是18，则DP的长是.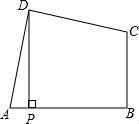
三、解答题
-
18.
如图，在△ABC中，点D是AB边上的中点，已知AC=4，BC=6，
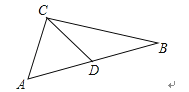(1)、画出△BCD关于点D的中心对称图形；
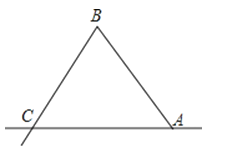
(2)、根据图形说明线段CD长的取值范围．19.现要在三角地ABC内建一中心医院，使医院到A、B两个居民小区的距离相等，并且到公路AB和AC的距离也相等，请确定这个中心医院的位置．
20. 已知：如图，P 是 OC 上一点，PD⊥OA 于 D，PE⊥OB 于 E，F，分别是 OA，B 上的点，且 PF=PG，DF=EG. 求证：OC 是∠AOB 的平分线.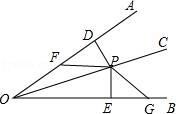
21.如图，在矩形ABCD中．点O在边AB上，∠AOC=∠BOD．求证：AO=OB．
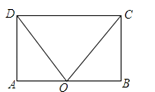22. 如图，E是▱ABCD的边CD的中点，延长AE交BC的延长线于点F.
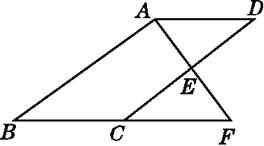(1)、求证：△ADE≌△FCE.(2)、若∠BAF=90°，BC=5，EF=3，求CD的长.
23. 如图所示，在△ABC中，∠C＝90°，AD是∠BAC的平分线，DE⊥AB交AB于E，F在AC上，BD＝DF.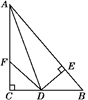
求证：
(1)、CF＝EB；(2)、AB＝AF＋2EB.24. 在Rt△ABC中，∠BAC= ，D是BC的中点，E是AD的中点.过点A作AF∥BC交BE的延长线于点F.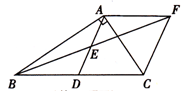
(1)、求证：△AEF≌△DEB；(2)、证明四边形ADCF是菱形；(3)、若AC=4，AB=5，求菱形ADCFD 的面积.25. 如图，在平面直角坐标系中，△AOB是直角三角形，∠AOB=90°，边AB与y轴交于点C.
(1)、若∠A=∠AOC，试说明：∠B=∠BOC；(2)、延长AB交x轴于点E，过O作OD⊥AB，若∠DOB=∠EOB，∠A=∠E，求∠A的度数；(3)、如图，OF平分∠AOM，∠BCO的平分线交FO的延长线于点P，∠A=40°，当△ABO绕O点旋转时（边AB与y轴正半轴始终相交于点C），问∠P的度数是否发生改变？若不变，求其度数；若改变，请说明理由.