安徽省淮南市2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2019-06-05 类型:期末考试
一、单选题
-
1. 以下列各组数据为边长,能构成三角形的是( )A、4,4,8 B、2,4,7 C、4,8,8 D、2,2,72. 一个凸多边形的内角和等于540°,则这个多边形的边数是( )A、5 B、6 C、7 D、83. 如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E,下列说法错误的是( )
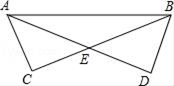 A、AD=BC B、∠DAB=∠CBA C、△ACE≌△BDE D、AC=CE4. 如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是( )
A、AD=BC B、∠DAB=∠CBA C、△ACE≌△BDE D、AC=CE4. 如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是( )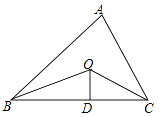 A、25 B、84 C、42 D、215. 下列图形中不是轴对称图形的是( )A、
A、25 B、84 C、42 D、215. 下列图形中不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 若x+y=2,xy=﹣2,则+的值是( )A、2 B、-2 C、4 D、-47. 下列等式从左到右的变形,属于因式分解的是A、(a+b)(a﹣b)=a2﹣b2 B、a2+4a+1=a(a+4)+1 C、x3﹣x=x(x+1)(x﹣1) D、8. 某煤矿原计划x天生产120t煤,由于采用新的技术,每天增加生存3t,因此提前2天完成,列出的方程为( )
6. 若x+y=2,xy=﹣2,则+的值是( )A、2 B、-2 C、4 D、-47. 下列等式从左到右的变形,属于因式分解的是A、(a+b)(a﹣b)=a2﹣b2 B、a2+4a+1=a(a+4)+1 C、x3﹣x=x(x+1)(x﹣1) D、8. 某煤矿原计划x天生产120t煤,由于采用新的技术,每天增加生存3t,因此提前2天完成,列出的方程为( )
A、 B、 C、 D、9. 下列算式中,你认为正确的是( ).A、 B、1÷ . =l C、 D、10. 已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,② AQ=BQ,③BP=2PQ, ④AE+BD=AB,其正确的个数有( )个. A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
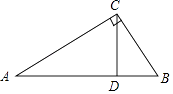
11. 当 = 时,分式 的值为0.12. 若多项式x2+ax﹣2分解因式的结果为(x+1)(x﹣2),则a的值为 .13. 如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,AB=8,则BC= , ∠BCD= , BD= .
 14. 如图,在△ABC中,AC=3,中线AD=5,则边AB的取值范围是 .
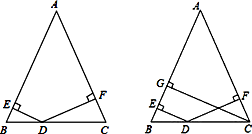
14. 如图,在△ABC中,AC=3,中线AD=5,则边AB的取值范围是 .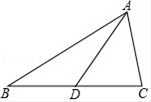 15. 如图,△ABC中,BD平分∠ABC , BC的中垂线交BC于点E , 交BD于点F , 连接CF . 若∠A=60°,∠ABD=24°,则∠ACF= .
15. 如图,△ABC中,BD平分∠ABC , BC的中垂线交BC于点E , 交BD于点F , 连接CF . 若∠A=60°,∠ABD=24°,则∠ACF= .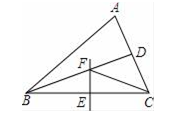 16. 如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB , 垂足为E , AD的垂直平分线交AB于点F , 则△DEF的面积为 .
16. 如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB , 垂足为E , AD的垂直平分线交AB于点F , 则△DEF的面积为 .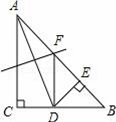 17. 若x-y≠0,x-2y=0,则分式 的值 .18. 如图,在△ABC与△AEF中,AB=AE , BC=EF , ∠B=∠E , AB交EF于点
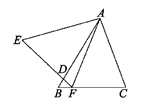
17. 若x-y≠0,x-2y=0,则分式 的值 .18. 如图,在△ABC与△AEF中,AB=AE , BC=EF , ∠B=∠E , AB交EF于点D.给出下列结论:①∠EAB=∠FAC;②AF=AC;③∠C=∠EFA;④AD=A
C.其中正确的结论是(填序号).
三、解答题
-
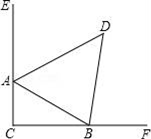
19. 先化简,再求值:[(x﹣2y)2﹣2y(2y﹣x)]÷2x , 其中 x=2,y=1.20. 已知x2+y2﹣4x+6y+13=0,求x2﹣6xy+9y2的值.21. 如图,在△ABC中,∠C=90°,外角∠EAB,∠ABF的平分线AD、BD相交于点D,求∠D的度数.
 22. 如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N,
22. 如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N,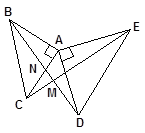
证明:
(1)、BD=CE.(2)、BD⊥CE.