重庆市江津区2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2019-06-05 类型:期末考试
一、单选题
-
1. 下列手机屏幕解锁图案中不是轴对称图形的是( )A、
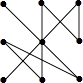 B、
B、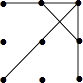 C、
C、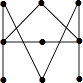 D、
D、 2. 以下列各组线段为边,能组成三角形的是( )A、2cm,3cm,5cm B、3cm,3cm,6cm C、5cm,8cm,2cm D、4cm,5cm,6cm3. 下列运算正确的是( )A、 B、 C、 D、4. 一枚一角硬币的直径约为 ,用科学记数法表示为( )A、 B、 C、 D、5. 下列各式从左到右的变形是因式分解的是( )
2. 以下列各组线段为边,能组成三角形的是( )A、2cm,3cm,5cm B、3cm,3cm,6cm C、5cm,8cm,2cm D、4cm,5cm,6cm3. 下列运算正确的是( )A、 B、 C、 D、4. 一枚一角硬币的直径约为 ,用科学记数法表示为( )A、 B、 C、 D、5. 下列各式从左到右的变形是因式分解的是( )
A、 B、 C、 D、6. 如图,点P是∠BAC的平分线AD上一点,PE AC于点E.已知∠BAC =60° ,PA=6,则PE长是( ) A、3 B、4 C、5 D、67. 已知△ABC的三个内角满足关系:∠A+∠B=∠C,则此三角形是( )A、等边三角形 B、锐角三角形 C、直角三角形 D、钝角三角形8. “五一”期间,东方中学“动感数学”活动小组的全体同学包租一辆面包车前去某景点游览,面包车的租价为180元.出发时又增加了两名同学,结果每个同学比原来少摊了3元车费.若设“动感数学”活动小组有x人,则所列方程为( )A、 B、 C、 D、9. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( )
A、3 B、4 C、5 D、67. 已知△ABC的三个内角满足关系:∠A+∠B=∠C,则此三角形是( )A、等边三角形 B、锐角三角形 C、直角三角形 D、钝角三角形8. “五一”期间,东方中学“动感数学”活动小组的全体同学包租一辆面包车前去某景点游览,面包车的租价为180元.出发时又增加了两名同学,结果每个同学比原来少摊了3元车费.若设“动感数学”活动小组有x人,则所列方程为( )A、 B、 C、 D、9. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( ) A、1个 B、2个 C、3个 D、4个10. 一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
A、1个 B、2个 C、3个 D、4个10. 一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )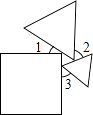 A、90° B、100° C、130° D、180°11. 分式 中,当 时,下列说法正确的是( )A、分式的值为零 B、分式无意义 C、若 时,分式的值为零 D、若 时,分式的值为零12. 如图所示,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,现有①点P在∠BAC的平分线上; ②AS=AR;③QP∥AR; ④△BRP≌△QSP四个结论.则对四个结论判断正确的是( )
A、90° B、100° C、130° D、180°11. 分式 中,当 时,下列说法正确的是( )A、分式的值为零 B、分式无意义 C、若 时,分式的值为零 D、若 时,分式的值为零12. 如图所示,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,现有①点P在∠BAC的平分线上; ②AS=AR;③QP∥AR; ④△BRP≌△QSP四个结论.则对四个结论判断正确的是( ) A、仅①和②正确 B、仅②③正确 C、仅①和③正确 D、全部都正确
A、仅①和②正确 B、仅②③正确 C、仅①和③正确 D、全部都正确二、填空题
-
13. 若点A( ,7)与点B(8, )关于 轴对称,则 .14. 因式分解: = .15. 如图,∠ABC=∠DCB,请补充一个条件: , 使△ABC≌△DCB.
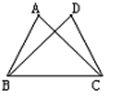 16. 如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积为12 ,则图中阴影部分的面积是
16. 如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积为12 ,则图中阴影部分的面积是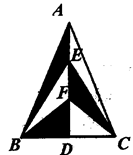 17. 如图,在△ABC中,将△ABC沿DE折叠,使顶点C落在△ABC三边的垂直平分线的交点O处,若BE=BO,则∠BOE=度.
17. 如图,在△ABC中,将△ABC沿DE折叠,使顶点C落在△ABC三边的垂直平分线的交点O处,若BE=BO,则∠BOE=度. 18. 如果记 ,并且f(1)表示当 时y的值,即f(1)= ;f( )表示当 时y的值,即f( )= .那么 .
18. 如果记 ,并且f(1)表示当 时y的值,即f(1)= ;f( )表示当 时y的值,即f( )= .那么 .三、解答题
-
19. 计算或化简:(1)、 ;(2)、 .20. 如图:点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AB∥DE.
求证:△ABC≌△DEF.
 21. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).
21. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1). (1)、在图中作出△ABC关于y轴对称的△A1B1C1 .(2)、写出A1 , B1 , C1的坐标,A1;B1;C1 . (直接写出答案)(3)、△A1B1C1的面积为 . (直接写出答案)22. 先化简再求值: ,其中 是不等式 的正整数解.23. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F.
(1)、在图中作出△ABC关于y轴对称的△A1B1C1 .(2)、写出A1 , B1 , C1的坐标,A1;B1;C1 . (直接写出答案)(3)、△A1B1C1的面积为 . (直接写出答案)22. 先化简再求值: ,其中 是不等式 的正整数解.23. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F. (1)、判断△BEO的形状,并说明理由.(2)、若AB=5cm,AC=4cm,求△AEF的周长.24. 目前,我区正在实施的“同城一体化”工程进展顺利区招投标中心在对观光路工程招标时,接到甲、乙两个工程队的投标书,甲、乙施工一天的工程费用分别为1.5万元和1.1万元,区招投标中心根据甲、乙两队的投标书测算,应有三种施工方案:
(1)、判断△BEO的形状,并说明理由.(2)、若AB=5cm,AC=4cm,求△AEF的周长.24. 目前,我区正在实施的“同城一体化”工程进展顺利区招投标中心在对观光路工程招标时,接到甲、乙两个工程队的投标书,甲、乙施工一天的工程费用分别为1.5万元和1.1万元,区招投标中心根据甲、乙两队的投标书测算,应有三种施工方案:⑴甲队单独做这项工程刚好如期完成;
⑵乙队单独做这项工程,要比规定日期多5天;
⑶若甲、乙两队合作4天后,余下的工程由乙队单独做,也正好如期完成.
在确保如期完成的情况下,你认为哪种方案最节省工程款,通过计算说明理由.
25. 已知CD是经过∠BCA顶点C的一条直线,CA=CB . E、F分别是直线CD上两点,且∠BEC=∠CFA=∠ . (1)、若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
(1)、若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:如图1若∠BCA=90°,∠ =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
(2)、如图2,若0°<∠BCA<180°, 请添加一个关于∠ 与∠BCA关系的条件使①中的结论仍然成立;(3)、如图3,若直线CD经过∠BCA的外部,∠ =∠BCA , 请写出三条线段EF、BE、AF的数量关系并证明你的结论.