安徽省巢湖市2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2019-06-05 类型:期末考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 若数据m,2,5,7,1,4,n的平均数为4,则m,n的平均数为( )A、7.5 B、5.5 C、2.5 D、4.53. 如果数据1,2,2,x的平均数与众数相同,那么x等于( )A、1 B、2 C、3 D、44. 以下二次根式:① ;② ;③ ;④ 中,与 是同类二次根式的是( )A、①和② B、②和③ C、①和④ D、③和④5. 分别以下列五组数为一个三角形的边长:①6,8,10;②13,5,12 ③1,2,3;④9,40,41;⑤3 ,4,5 .其中能构成直角三角形的有( )组A、2 B、3 C、4 D、56. 如图,分别以直角△ABC的三边AB , BC , CA为直径向外作半圆,面积记为S1、S2、S3 , 则( )
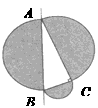 A、S1>S2+S3 B、S1= S2+S3 C、S1< S2+S3 D、无法确定7. 如图所示,AB=BC=CD=DE=1,AB⊥BC , AC⊥CD , AD⊥DE , 则AE=( )
A、S1>S2+S3 B、S1= S2+S3 C、S1< S2+S3 D、无法确定7. 如图所示,AB=BC=CD=DE=1,AB⊥BC , AC⊥CD , AD⊥DE , 则AE=( ) A、1 B、 C、 D、28. 若直线y=kx+b中,k<0,b>0,则直线不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 为保护生态环境,陕西省某县响应国家“退耕还林”号召,将某一部分耕地改为林地,改变后,林地面积和耕地面积共有180平方千米,耕地面积是林地面积的25%,为求改变后林地面积和耕地面积各多少平方千米.设改变后耕地面积x平方千米,林地地面积y平方千米,根据题意,列出如下四个方程组,其中正确的是( )A、 B、 C、 D、10. 若方程组 的解满足 ,则m的取值范围是( )A、m>-6 B、m<6 C、m<-6 D、m>6
A、1 B、 C、 D、28. 若直线y=kx+b中,k<0,b>0,则直线不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 为保护生态环境,陕西省某县响应国家“退耕还林”号召,将某一部分耕地改为林地,改变后,林地面积和耕地面积共有180平方千米,耕地面积是林地面积的25%,为求改变后林地面积和耕地面积各多少平方千米.设改变后耕地面积x平方千米,林地地面积y平方千米,根据题意,列出如下四个方程组,其中正确的是( )A、 B、 C、 D、10. 若方程组 的解满足 ,则m的取值范围是( )A、m>-6 B、m<6 C、m<-6 D、m>6二、填空题
-
11. 若一组数据6,7,5,6,x,1的平均数是5,则这组数据的众数是 .12. 如图,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有米。
 13. 某小组某次英语听写的平均成绩为80分,5名同学中有4名同学的成绩分别为:82,85,90,75,则另一名同学的成绩为分。14. 实数 在数轴上的位置如图所示:
13. 某小组某次英语听写的平均成绩为80分,5名同学中有4名同学的成绩分别为:82,85,90,75,则另一名同学的成绩为分。14. 实数 在数轴上的位置如图所示: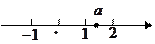
化简: =。
15. 若点P(a,b)在第二象限内,则直线y=ax+b不经过第象限.16. 当m时,一次函数y=(m+1)x+6的函数值随x的增大而减小.17. 若方程组 的解满足方程 ,则a的值为.18. 如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F,若BE=2,则CF长为。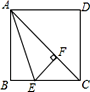 19. 设 表示大于 的最小整数,如 , ,则下列结论中正确的是。(填写所有正确结论的序号)① ;② 的最小值是0;③ 的最大值是0;④存在实数 ,使 成立。
19. 设 表示大于 的最小整数,如 , ,则下列结论中正确的是。(填写所有正确结论的序号)① ;② 的最小值是0;③ 的最大值是0;④存在实数 ,使 成立。三、解答题
-
20. 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 , ,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,求这个风车的外围周长.
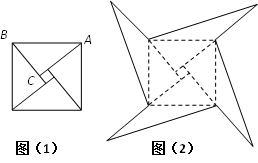 21. 化简下列各式。(1)、(2)、 ;22. 先化简、再求值。(6x + )-(4x+ ),其中x= ,y=27.23. 下图反映了八年级(2)班40名学生在一次数学测验的成绩。
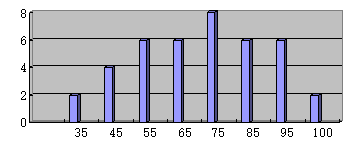
21. 化简下列各式。(1)、(2)、 ;22. 先化简、再求值。(6x + )-(4x+ ),其中x= ,y=27.23. 下图反映了八年级(2)班40名学生在一次数学测验的成绩。① 从图中观察这个班这次数学测验成绩的中位数和众数。
② 根据图形估计这个班这次数学测验成绩的平均成绩。
 24. 已知y﹣2与x成正比,且当x=1时,y=﹣6,(1)、求y与x之间的函数关系式;(2)、若点(a,2)在这个函数图象上,求a.25. 如图,在直角坐标系中,直线y=kx+4与x 轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求这条直线的解析式。
24. 已知y﹣2与x成正比,且当x=1时,y=﹣6,(1)、求y与x之间的函数关系式;(2)、若点(a,2)在这个函数图象上,求a.25. 如图,在直角坐标系中,直线y=kx+4与x 轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求这条直线的解析式。 26. 已知一次函数y=kx+b的图象经过点(-1, -5),且与正比例函数y= x的图象相交于点(2,a),求:(1)、a的值(2)、k,b的值(3)、这两个函数图象与y轴所围成的三角形的面积。27. 先阅读下列的解答过程,然后作答:
26. 已知一次函数y=kx+b的图象经过点(-1, -5),且与正比例函数y= x的图象相交于点(2,a),求:(1)、a的值(2)、k,b的值(3)、这两个函数图象与y轴所围成的三角形的面积。27. 先阅读下列的解答过程,然后作答:形如 的化简,只要我们找到两个数a、b使a+b=m,ab=n,这样( )2+( )2=m · =n,那么便有 = = ± (a>b) .例如:化简 解:首先把 化为 ,这里m=7,n=12;由于4+3=7,4×3=12,即( )2+( )2=7 · = ,
∴ = = =2+ .
由上述例题的方法化简:
(1)、(2)、(3)、28. 清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S , 则第一步: =m;第二步: =k;第三步:分别用3、4、5乘以k , 得三边长”.(1)、当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;(2)、你能证明“积求勾股法”的符合题意性吗?请写出证明过程.