云南省曲靖市罗平县2015-2016学年八年级下学期数学期末考试试卷
试卷更新日期:2019-06-05 类型:期末考试
一、单选题
-
1. 下列各曲线中,不能表示y是x的函数的是( )A、
 B、
B、 C、
C、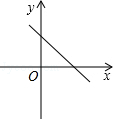 D、
D、 2. 下列命题中,逆命题是真命题的是( )A、直角三角形的两锐角互余 B、对顶角相等 C、若两直线垂直,则两直线有交点 D、若3. 函数y= 中,自变量x的取值范围是( )A、x≠0 B、x≥2 C、x>2且x≠0 D、x≥2且x≠04. 2015年1月1日起,杭州市城区实行全新的阶梯水价,之前为了解某社区居民的用水情况,随机对该社区20户居民进行了调查,下表是这20户居民2014年8月份用水量的调查结果:那么关于这次用水量的调查和数据分析,下列说法错误的是( )
2. 下列命题中,逆命题是真命题的是( )A、直角三角形的两锐角互余 B、对顶角相等 C、若两直线垂直,则两直线有交点 D、若3. 函数y= 中,自变量x的取值范围是( )A、x≠0 B、x≥2 C、x>2且x≠0 D、x≥2且x≠04. 2015年1月1日起,杭州市城区实行全新的阶梯水价,之前为了解某社区居民的用水情况,随机对该社区20户居民进行了调查,下表是这20户居民2014年8月份用水量的调查结果:那么关于这次用水量的调查和数据分析,下列说法错误的是( )居民(户)
1
2
8
6
2
1
月用水量(吨)
4
5
8
12
15
20
A、平均数是10(吨) B、众数是8(吨) C、中位数是10(吨) D、样本容量是205. 如图l1:y=x+3与l2:y=ax+b相交于点P(m,4),则关于x的不等式x+3≤ax+b的解为( ) A、x≥4 B、x<m C、x≥m D、x≤16. 如图,E是正方形ABCD的边BC的延长线上一点,若CE=CA,AE交CD于F,则∠FAC的度数是( )
A、x≥4 B、x<m C、x≥m D、x≤16. 如图,E是正方形ABCD的边BC的延长线上一点,若CE=CA,AE交CD于F,则∠FAC的度数是( ) A、22.5° B、30° C、45° D、67.5°7. 已知:|a|=3,=5,且|a+b|=a+b,则a﹣b的值为( )A、2或8 B、2或﹣8 C、﹣2或8 D、﹣2或﹣88. 如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB= BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE= BC,成立的个数有( )
A、22.5° B、30° C、45° D、67.5°7. 已知:|a|=3,=5,且|a+b|=a+b,则a﹣b的值为( )A、2或8 B、2或﹣8 C、﹣2或8 D、﹣2或﹣88. 如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB= BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE= BC,成立的个数有( )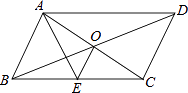 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. ﹣ ﹣ × + = .10. 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于 .
 11. 直线y=﹣2x+m﹣3的图象经过x轴的正半轴,则m的取值范围为 .12. 如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是 .
11. 直线y=﹣2x+m﹣3的图象经过x轴的正半轴,则m的取值范围为 .12. 如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是 . 13. 若函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,则a= .14. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是 .
13. 若函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,则a= .14. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是 .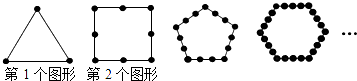
三、解答题
-
15. 计算:(1)、 ;(2)、( )2﹣(3+ )(3﹣ ).16. 先化简,再求值: ,其中x= ﹣1.17. 某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
分数(分)
人数(人)
70
7
80
90
1
100
8
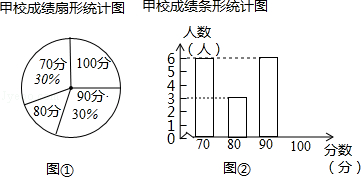 (1)、在图①中,“80分”所在扇形的圆心角度数为;(2)、请你将图②补充完整;(3)、求乙校成绩的平均分;(4)、经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.18. 如图,出租车是人们出行的一种便利交通工具,折线ABC是在我市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
(1)、在图①中,“80分”所在扇形的圆心角度数为;(2)、请你将图②补充完整;(3)、求乙校成绩的平均分;(4)、经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.18. 如图,出租车是人们出行的一种便利交通工具,折线ABC是在我市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.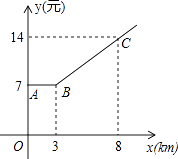 (1)、根据图象,当x≥3时y为x的一次函数,请写出函数关系式;
(1)、根据图象,当x≥3时y为x的一次函数,请写出函数关系式;
(2)、某人乘坐13km,应付多少钱?(3)、若某人付车费42元,出租车行驶了多少千米?19. 如图,在平面直角坐标系中,已知点A(3,4),B(﹣3,0). (1)、只用直尺(没有刻度)和圆规按下列要求作图.
(1)、只用直尺(没有刻度)和圆规按下列要求作图.(要求:保留作图痕迹,不必写出作法)
Ⅰ)AC⊥y轴,垂足为C;
Ⅱ)连结AO,AB,设边AB,CO交点E.
(2)、在(1)作出图形后,直接判断△AOE与△BOE的面积大小关系.20. 如图,在△ABC中,AD=15,AC=12,DC=9,点B是CD延长线上一点,连接AB,若AB=20.求:△ABD的面积.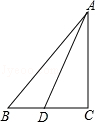 21. 如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是OB,OD的中点,试说明四边形AECF是平行四边形.
21. 如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是OB,OD的中点,试说明四边形AECF是平行四边形.