湖南省郴州市桂阳县2015-2016学年八年级下学期数学期末考试试卷
试卷更新日期：2019-06-05 类型：期末考试
一、单选题
-
1. 若点A（2，4）在函数y=kx的图象上，则下列各点在此函数图象上的是（ ）A、（1，2） B、（﹣2，﹣1） C、（﹣1，2） D、（2，﹣4）2. 在下列交通标志中，既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
3. 在平面直角坐标系中，点P（﹣3，4）关于y轴对称点的坐标为（ ）A、（﹣3，4） B、（3，4） C、（3，﹣4） D、（﹣3，﹣4）4. 已知▱ABCD的周长为32，AB=4，则BC=（ ）A、4 B、12 C、24 D、285. 正八边形的每个内角为（ ）A、120° B、135° C、140° D、144°6. 正六边形具备而菱形不具备的性质是（ ）A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、每条对角线平分一组对边7. 在Rt△ABC中，∠C=90°，AC=9，BC=12，则C点到AB的距离为（ ）A、 B、 C、 D、8. 一次函数y=ax+1与y=bx﹣2的图象交于x轴上同一个点，那么a：b等于（ ）A、1：2 B、（﹣1）：2 C、3：2 D、以上都不对二、填空题
-
9. 在Rt△ABC中，∠C=90°，斜边上的中线CD=3，则斜边AB的长是 ．10. 在Rt△ABC中，∠C=90°，∠B=30°，AB=16，则AC= ．11. 已知菱形的周长为40，两对角线比为3：4，则两对角线的长分别为 ．12. 一次函数的图象过点（0，3）且与直线y=﹣x平行，那么函数解析式是 ．13. 一个平行四边形的一条边长为3，两条对角线的长分别为4和2 ，则它的面积为 ．14. 如图，一块矩形纸片的宽CD为2cm，点E在AB上，如果沿图中的EC对折，B点刚好落在AD上，此时∠BCE=15°，则BC的长为 ．
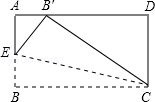15. 如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A，B的坐标分别为（﹣3，0），（2，0），点D在y轴上，则点C的坐标是 ．
16. 如图，在平面直角坐标系中，矩形OABC的对角线AC平行于x轴，边OA与x轴正半轴的夹角为30°，OC=2，则点A的坐标是 ．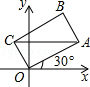
三、解答题
-
17. 已知：一次函数y=kx+b的图象经过M（0，2），N（1，3）两点．(1)、求k、b的值；(2)、若一次函数y=kx+b的图象与x轴交点为A（a，0），求a的值．18. 已知一次函数y=（m+3）x+m﹣4，y随x的增大而增大．(1)、求m的取值范围；(2)、如果这个一次函数又是正比例函数，求m的值．19. 如图，四边形ABCD四个顶点的坐标分别是A（1，2），B（3，1），C（5，2），D（3，4）．将四边形ABCD先向下平移5个单位，再向左平移6个单位，它的像是四边形A′B′C′D′．
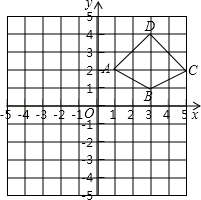(1)、作出四边形A′B′C′D′．(2)、写出四边形A′B′C′D′的顶点坐标．20. 如图，已知四边形ABCD是平行四边形，P、Q是对角线BD上的两个点，且AP∥QC．求证：BP=DQ．
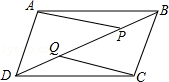21. 如图，在四边形ABCD中，AB=CD，M、N、E、F分别为AD、BC、BD、AC的中点，求证：四边形MENF为菱形．
22. 如图，△ABC中，AB=AC，AD⊥BC于点D，AE是∠BAC外角平分线，BE⊥AE，连接DE．
(1)、求证：DA⊥AE；(2)、求证：四边形DCAE是平行四边形．23. 某区在实施居民用水额定管理前，对居民生活用水情况进行了调查，下表是通过简单随机抽样获得的50个家庭去年月平均用水量（单位：吨），并将调查数据进行如下整理：4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
分组
划记
频数
2.0＜x≤3.5
正正
11
3.5＜x≤5.0
正正正正
19
5.0＜x≤6.5
6.5＜x≤8.0
8.0＜x≤9.5
合计
2
50
(1)、把上面频数分布表和频数分布直方图补充完整；(2)、从直方图中你能得到什么信息？（写出两条即可）；(3)、为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费，若要使60%的家庭收费不受影响，你觉得家庭月均用水量应该定为多少？为什么？24. 如图，直线y=﹣ x+8与x轴、y轴分别相交于点A、B，设M是OB上一点，若将△ABM沿AM折叠，使点B恰好落在x轴上的点B′处．求：
(1)、点B′的坐标；(2)、直线AM所对应的函数关系式．25. 一辆轿车从甲地驶往乙地，到达乙地后返回甲地，速度是原来的1.5倍，共用t小时．设轿车行驶的时间为x（h），轿车到甲地的距离为y（km），轿车行驶过程中y与x之间的函数图象如图．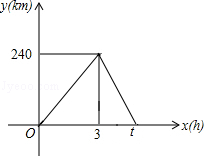
(1)、求轿车从乙地返回甲地时的速度和t的值；(2)、求轿车从乙地返回甲地时y与x之间的函数关系式，并写出自变量x的取值范围．26. 如图，直线l与坐标轴分别交于A、B两点，∠BAO=45°，点A坐标为（8，0）．动点P从点O出发，沿折线段OBA运动，到点A停止；同时动点Q也从点O出发，沿线段OA运动，到点A停止；它们的运动速度均为每秒1个单位长度．
(1)、求直线AB的函数关系式；(2)、若点A、B、O与平面内点E组成的图形是平行四边形，请直接写出点E的坐标；
(3)、在运动过程中，当P、Q的距离为2时，求点P的坐标．