2016-2017学年云南省楚雄州姚安一中高一下学期期中数学试卷

试卷更新日期：2017-05-25 类型：期中考试

进入出卷网下载

一、选择题

1. 1001101_（₂_）与下列哪个值相等（）

A、115_（₈_） B、113_（₈_） C、116_（₈_） D、114_（₈_）

查看试题解析
2. 将一枚硬币抛两次，恰好出现一次正面的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
3. ﹣1060^o的终边落在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 若sinα＜0且tanα＞0，则α是（　　）

A、第一象限角 B、第二象限角 C、第三象限角 D、第四象限角

查看试题解析
5. 圆心在y轴上，半径为1，且过点（1，2）的圆的方程为（　　）

A、x²+（y﹣2）²=1 B、x²+（y+2）²=1 C、（x﹣1）²+（y﹣3）²=1 D、x²+（y﹣3）²=1

查看试题解析
6. 已知直线l的方程为3x+4y﹣25=0，则圆x²+y²=1上的点到直线l的最大距距离是（）

A、1 B、4 C、5 D、6

查看试题解析
7. 图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a，b，i的值分别为8，10，0，则输出的a和i和值分别为（）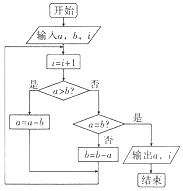

A、2，5 B、2，4 C、0，4 D、0，5

查看试题解析
8. 若三条直线l₁：ax+2y+6=0，l₂：x+y﹣4=0，l₃：2x﹣y+1=0相交于同一点，则实数a=（）

A、﹣12 B、﹣10 C、10 D、12

查看试题解析
9. 从500件产品中随机抽取20件进行抽样，利用随机数表法抽取样本时，先将这500件产品按001，002，003，…，500进行编号，如果从随机数表的第1行第6列开始，从左往右依次选取三个数字，则选出来的第4个个体编号为（）
1622 7794 3949 5443 5482 1737 9323 7887 3520 9643
8626 3491 6484 4217 5331 5724 5506 8877 0474 4767．

A、435 B、482 C、173 D、237

查看试题解析
10. 若α是第一象限的角，则 $\frac{α}{2}$ 所在的象限是（）

A、第一象限 B、第一、二象限 C、第一、三象限 D、第一、四象限

查看试题解析
11. 若点P（1，1）为圆（x﹣3）²+y²=9的弦MN的中点，则弦MN所在直线方程为（）

A、2x+y﹣3=0 B、x﹣2y+1=0 C、x+2y﹣3=0 D、2x﹣y﹣1=0

查看试题解析
12. 欧阳修在《卖油翁》中写到：“（翁）乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿”，可见卖油翁的技艺之高超，若铜钱直径2百米，中间有边长为1百米的正方形小孔，随机向铜钱上滴一滴油（油滴大小忽略不计），则油恰好落入孔中的概率是（）

A、 $\frac{1}{4 π}$ B、 $\frac{1}{2 π}$ C、 $\frac{1}{π}$ D、 $\frac{2}{π}$

查看试题解析

二、二.填空题：

13. 某个年级有男生560人，女生420人，用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本，则此样本中男生人数为．

查看试题解析
14. 已知sinα= $\frac{4}{5}$ ，且α是第二象限角，那么tanα的值是．

查看试题解析
15. 用秦九韶算法求多项式f（x）=3x⁴+2x²+x+4当x=10时的值的过程中，V₁的值等于

查看试题解析
16. 若直线x﹣y﹣2=0被圆（x﹣a）²+y²=4所截得的弦长为 $2 \sqrt{2}$ ，则实数a的值为．

查看试题解析

三、解答题

17. 已知圆：x²+y²+x﹣6y+3=0与直线x+2y﹣3=0的两个交点为P、Q，求以P，Q为直径的圆的方程．

查看试题解析
18. 已知圆C的方程为（x﹣1）²+（y﹣2）²=4．
（Ⅰ）求过点M（3，1）的圆C的切线方程；
（Ⅱ）判断直线ax﹣y+3=0与圆C的位置关系．

查看试题解析
19. 心理健康教育老师对某班50个学生进行了心里健康测评，测评成绩满分为100分．成绩出来后，老师对每个成绩段的人数进行了统计，并得到如图4所示的频率分布直方图．

(1)、求a，并从频率分布直方图中求出成绩的众数和中位数；

(2)、若老师从60分以下的人中选两个出来与之聊天，则这两人一个在（40，50]这一段，另一个在（50，60]这一段的概率是多少？

查看试题解析
20. 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83．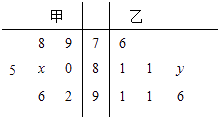

(1)、求x和y的值；

(2)、计算甲班7位学生成绩的方差s²；

(3)、从成绩在90分以上的学生中随机抽取两名学生，求甲班至少有一名学生的概率．

查看试题解析
21. 某小组共有A、B、C、D、E五位同学，他们的身高（单位：米）以及体重指标（单位：千克/米²）如表所示：
A
B
C
D
E
身高
1.69
1.73
1.75
1.79
1.82
体重指标
19.2
25.1
18.5
23.3
20.9
（Ⅰ）从该小组身高低于1.80的同学中任选2人，求选到的2人身高都在1.78以下的概率
（Ⅱ）从该小组同学中任选2人，求选到的2人的身高都在1.70以上且体重指标都在[18.5，23.9）中的概率．

查看试题解析
22. 随着我国经济的发展，居民的储蓄存款逐年增长．设某地区城乡居民人民币储蓄存款（年底余额）如下表：
年份
2010
2011
2012
2013
2014
时间代号t
1
2
3
4
5
储蓄存款y（千亿元）
5
6
7
8
10
（Ⅰ）求y关于t的回归方程 $\hat{y}$ = $\hat{b}$ t+ $\hat{a}$ ．
（Ⅱ）用所求回归方程预测该地区2015年（t=6）的人民币储蓄存款．
附：回归方程 $\hat{y}$ = $\hat{b}$ t+ $\hat{a}$ 中
${\begin{cases} b = \frac{\sum_{i = 1}^{n} (t_{i} - \bar{t}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(t_{i} - \bar{t})}^{2}} \\ a = \bar{y} - b \bar{t} \end{cases} = \frac{\sum_{i = 1}^{n} t_{i} y_{i} - n \bar{t} \bar{y}}{\sum_{i = 1}^{n} t_{i}^{2} - n {\bar{t}}^{2}}$ ．

查看试题解析

	A	B	C	D	E
身高	1.69	1.73	1.75	1.79	1.82
体重指标	19.2	25.1	18.5	23.3	20.9

年份	2010	2011	2012	2013	2014
时间代号t	1	2	3	4	5
储蓄存款y（千亿元）	5	6	7	8	10