2016-2017学年江苏省盐城市盐都区九年级下学期期中数学试卷
试卷更新日期:2017-05-25 类型:期中考试
一、选择题
-
1. 的倒数是( )A、﹣3 B、 C、3 D、2. 下列计算正确的是( )A、2a﹣a=1 B、a2+a2=2a4 C、a2•a3=a5 D、(a﹣b)2=a2﹣b23. 不等式组 的解集是( )A、x>1 B、1<x≤2 C、x≤2 D、无解4. 一个几何体的三视图如图所示,则这个几何体是( )
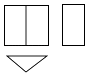 A、
A、 B、
B、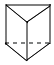 C、
C、 D、
D、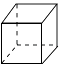 5. 对于一组统计数据:3,3,6,3,5,下列说法中错误的是( )A、中位数是6 B、众数是3 C、平均数是4 D、方差是1.66. 如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
5. 对于一组统计数据:3,3,6,3,5,下列说法中错误的是( )A、中位数是6 B、众数是3 C、平均数是4 D、方差是1.66. 如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )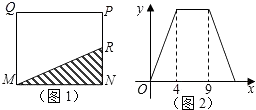 A、当x=2时,y=5 B、矩形MNPQ的面积是20 C、当x=6时,y=10 D、当y= 时,x=3
A、当x=2时,y=5 B、矩形MNPQ的面积是20 C、当x=6时,y=10 D、当y= 时,x=3二、填空题
-
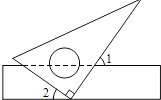
7. 若二次根式 有意义,则x的取值范围是 .8. “十二五”期间,将新建保障性住房约37000000套,用于解决中低收入和新参加工作的大学生住房的需求,把37000000用科学记数法表示应该是 .9. 如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为°.
 10. 小燕抛一枚硬币10次,有7次正面朝上,当她抛第11次时,正面向上的概率为 .11. 如图,⊙O的内接四边形ABCD中,∠BOD=100°,则∠BCD= .
10. 小燕抛一枚硬币10次,有7次正面朝上,当她抛第11次时,正面向上的概率为 .11. 如图,⊙O的内接四边形ABCD中,∠BOD=100°,则∠BCD= .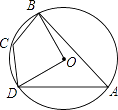 12. 若a﹣2b=2,则6﹣3a+6b的值为 .13. 三翼式旋转门在圆柱形的空间内旋转,旋转内的三片旋转翼把空间等分成三个部分,如图1,旋转门的俯视图是直径的2米的圆,图2显示了某一时刻旋转翼的位置,则弧AB的长是米.(结果保留π)
12. 若a﹣2b=2,则6﹣3a+6b的值为 .13. 三翼式旋转门在圆柱形的空间内旋转,旋转内的三片旋转翼把空间等分成三个部分,如图1,旋转门的俯视图是直径的2米的圆,图2显示了某一时刻旋转翼的位置,则弧AB的长是米.(结果保留π)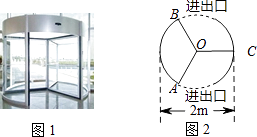 14. 如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为 .
14. 如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为 .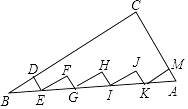 15. 定义:如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”.若Rt△ABC为匀称三角形,且∠C=90°,AC=4,则BC= .16. 如图,已知A1 , A2 , A3 , …An是x轴上的点,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1 , A2 , A3 , …An作x轴的垂线交反比例函数y= (x>0)的图象于点B1 , B2 , B3 , …Bn , 过点B2作B2P1⊥A1B1于点P1 , 过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1 , △B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn , 则S1+S2+S3+…+Sn= .
15. 定义:如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”.若Rt△ABC为匀称三角形,且∠C=90°,AC=4,则BC= .16. 如图,已知A1 , A2 , A3 , …An是x轴上的点,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1 , A2 , A3 , …An作x轴的垂线交反比例函数y= (x>0)的图象于点B1 , B2 , B3 , …Bn , 过点B2作B2P1⊥A1B1于点P1 , 过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1 , △B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn , 则S1+S2+S3+…+Sn= .
三、解答题
-
17. 计算:|﹣8|+(﹣2)3+tan45°﹣ .18. 先化简,再求值:(1+ )÷ ,其中x= ﹣1.19. 如图,转盘被等分成6个扇形,每个扇形上依次标有数字1,2,3,4,5,6.在游戏中特别规定:当指针指向边界时,重新转动转盘.
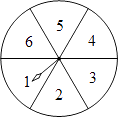 (1)、自由转动转盘,当它停止转动时,指针指向的数大于4的概率为;(2)、请用画树状图法或列表法等方式求出“两次转动转盘,指针指向的数都大于4”的概率.20. 某学校九年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置一、二、三等奖各进步奖共四个奖项,赛后将九年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请根据图中的信息,解答下列问题:
(1)、自由转动转盘,当它停止转动时,指针指向的数大于4的概率为;(2)、请用画树状图法或列表法等方式求出“两次转动转盘,指针指向的数都大于4”的概率.20. 某学校九年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置一、二、三等奖各进步奖共四个奖项,赛后将九年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请根据图中的信息,解答下列问题: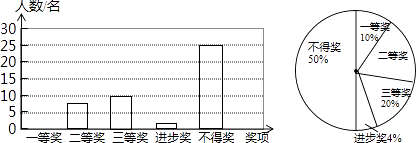 (1)、九年级(1)班共有名学生;(2)、将条形图补充完整:在扇形统计图中,“二等奖”对应的扇形的圆心角度数是;(3)、如果该九年级共有1250名学生,请估计荣获一、二、三等奖的学生共有多少名.21. 如图,在▱ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.
(1)、九年级(1)班共有名学生;(2)、将条形图补充完整:在扇形统计图中,“二等奖”对应的扇形的圆心角度数是;(3)、如果该九年级共有1250名学生,请估计荣获一、二、三等奖的学生共有多少名.21. 如图,在▱ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.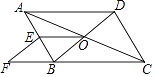 (1)、求证;四边形OBFE是平行四边形;(2)、当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由.22. 如图,AB是⊙O的直径,D为⊙O上一点,过 上一点T作⊙O的切线TC,且TC⊥AD于点C.
(1)、求证;四边形OBFE是平行四边形;(2)、当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由.22. 如图,AB是⊙O的直径,D为⊙O上一点,过 上一点T作⊙O的切线TC,且TC⊥AD于点C.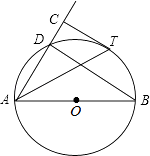 (1)、若∠DAB=50°,求∠ATC的度数;(2)、若⊙O半径为2,CT= ,求AD的长.23. 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y= (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3, ).
(1)、若∠DAB=50°,求∠ATC的度数;(2)、若⊙O半径为2,CT= ,求AD的长.23. 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y= (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3, ).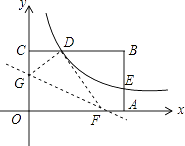 (1)、求反比例函数的表达式和m的值;(2)、将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式.24. 如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图(图2),支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得DE=20厘米,DC=40厘米,∠AED=58°,∠ADE=76°.
(1)、求反比例函数的表达式和m的值;(2)、将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式.24. 如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图(图2),支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得DE=20厘米,DC=40厘米,∠AED=58°,∠ADE=76°. (1)、求椅子的高度(即椅子的座板DF与地面MN之间的距离)(精确到1厘米)(2)、求椅子两脚B、C之间的距离(精确到1厘米)(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin76°≈0.97.cos76°≈0.24,tan76°≈4.00)25. 某公司开发出一种高科技电子节能产品,投资2500万元一次性购买整套生产设备,此外生产每件产品需成本20元,每年还需投入500万广告费,按规定该产品的售价不得低于30元/件且不得高于70元/件,该产品的年销售量y(万件)与售价x(元/件)之间的函数关系如下表:
(1)、求椅子的高度(即椅子的座板DF与地面MN之间的距离)(精确到1厘米)(2)、求椅子两脚B、C之间的距离(精确到1厘米)(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin76°≈0.97.cos76°≈0.24,tan76°≈4.00)25. 某公司开发出一种高科技电子节能产品,投资2500万元一次性购买整套生产设备,此外生产每件产品需成本20元,每年还需投入500万广告费,按规定该产品的售价不得低于30元/件且不得高于70元/件,该产品的年销售量y(万件)与售价x(元/件)之间的函数关系如下表:x(元/件)
30
31
…
70
y(万件)
120
119
…
80
(1)、求y与x的函数关系式,并写出x的取值范围;(2)、第一年公司是盈利还是亏损?冰球出当盈利最大或亏损最小时该产品的售价;(3)、在(2)的前提下,即在第一年盈利最大或亏损最小时,第二年公司重新确定产品定价,能否使两年盈利3500万元?若能,求第二年产品的售价;若不能,说明理由.26. 探究题(1)、问题发现如图1,△ABC和△BDE均为等边三角形,点A,D,E在同一直线上,连接CD.填空;
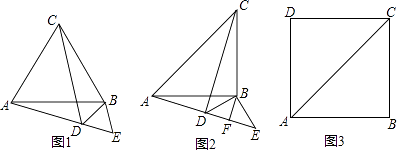
①CDB的度数为;
②线段AE,CD之间的数量关系为 .
(2)、拓展探究如图2,△ABC和△DBE均为等腰直角三角形,∠ABC=∠DBE=90°,点A,D,E在同一直线上,BF为△DBE中DE边上的高,连接CD.
①求∠CDB的大小;
②请判断线段BF,AD,CD之间的数量关系,并说明理由.
(3)、解决问题如图3,在正方形ABCD中,AC=2 ,AE=1,CE⊥AE于E,请补全图形,求点B到CE的距离.
27. 如图1,二次函数y= x2+bx+c与一次函数y= x﹣3的图象都经过x轴上点A(4,0)和y轴上点B(0,﹣3),过动点M(m,0)(0<m<4)作x轴的垂线交直线AB于点C,交抛物线于点P.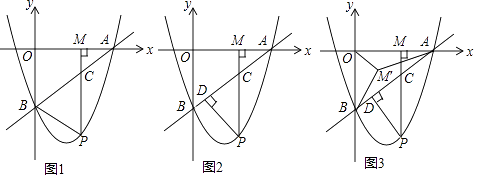 (1)、求b,c的值;(2)、点M在运动的过程中,能否使△PBC为直角三角形?如果能,求出点P的坐标;如果不能,请说明理由;(3)、如图2,过点P作PD⊥AB于点,设△PCD的面积为S1 , △ACM的面积为2 , 若 = ,
(1)、求b,c的值;(2)、点M在运动的过程中,能否使△PBC为直角三角形?如果能,求出点P的坐标;如果不能,请说明理由;(3)、如图2,过点P作PD⊥AB于点,设△PCD的面积为S1 , △ACM的面积为2 , 若 = ,①求m的值;
②如图3,将线段OM绕点O顺时针旋转得到OM′,旋转角为α(0°<α<90°),连接M'A、M'B,求M'A+ M'B的最小值.