2016-2017学年江苏省盐城市建湖县九年级下学期期中数学试卷

试卷更新日期：2017-05-25 类型：期中考试

进入出卷网下载

一、选择题

1. ﹣1是1的（）

A、倒数 B、相反数 C、绝对值 D、立方根

查看试题解析
2. 计算正确的是（）

A、（a+b）²=a²+b² B、x²+x³=x⁵ C、（ab²）³=a²b⁵ D、2a²•a^﹣¹=2a

查看试题解析
3. 如图是由5个相同的小正方体组成的立体图形，这个立体图形的俯视图是（）

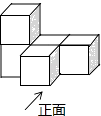A、 B、 C、 D、

查看试题解析
4. 如图，在△ABC中，AB=AC，AD∥BC，若∠BAD=110°，则∠BCA的大小为（）

A、30° B、40° C、50° D、70°

查看试题解析
5. 如图，边长为1的小正方形网格中，⊙O的圆心在格点上，则∠AED的正弦值是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
6.
如图，正方形ABCD的边长为4，点P为BC边上的任意一点（不与点B、C重合），且∠DPE=90°，PE交AB于点E，设BP=x，BE=y，则y关于x的函数图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 若式子 $\frac{x}{x - 3}$ 有意义，则x的取值范围是．

查看试题解析
8. 因式分解：2a²﹣8a+8= ．

查看试题解析
9. 被誉为“里下河的明珠”的九龙口自然保护区，地处射阳湖腹部的建湖县九龙口镇，由蚬河等9条自然河道汇集而成，水面约6670万平方米，这里藏垒水禽野味，广植柴蒲菱藕，盛产鱼虾螃蟹，有“金滩银荡”之美誉，是天然的“聚宝盆”，其中6670万平方米用科学记数法表示为平方米．

查看试题解析
10. 一组数据3，4，5，x，7，8的平均数为6，则这组数据的方差是．

查看试题解析
11. 如图，四边形ABCD的对角线AC、BD相交于点O，△ABO≌△ADO．下列结论：
①AC⊥BD；②CB=CD；③△ABC≌△ADC；④DA=DC．
其中所有正确结论的序号是．

查看试题解析
12. 已知方程组 ${\begin{cases} 3 x + y = 1 + 3 m \\ x + 3 y = 1 - m \end{cases}$ 的解x+y＞0，则m的取值范围是．

查看试题解析
13. 已知关于x的方程x²﹣mx+6=0的一个解是x=﹣2，则方程的另一个解是．

查看试题解析
14. 如图，已知正六边形ABCDEF没接于半径为4的⊙O，则B、D两点间的距离为．

查看试题解析
15. 如图，在四边形ABCD中，∠ABC=30°，将△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE，若AB=3，BC=4，则BD=（提示：可连接BE）

查看试题解析
16. 如图，P为反比例函数y= $\frac{3}{2 x}$ （x＞0）图象上一点，过点P分别向x轴，y轴作垂线，垂足分别为M、N，直线y=﹣x+2与PM、PN分别交于点E、F，与x轴、y轴分别交于A、B，则AF•BE的值为．

查看试题解析

三、解答题

17. 计算：（π﹣2017）⁰+ $\sqrt{2}$ cos45°﹣|﹣3|+（ $\frac{1}{2}$ ）^﹣¹ ．

查看试题解析
18. 先化简（ $\frac{2}{a + 1}$ ﹣ $\frac{2 a - 3}{a^{2} - 1}$ ）÷ $\frac{1}{a + 1}$ ，然后再从﹣2＜a≤2的范围内选取一个合适的a的整数值代入求值．

查看试题解析
19. 已知：关于x的一元二次方程x²+2x+k=0有两个不相等的实数根．

(1)、求k的取值范围；

(2)、当k取最大整数值时，用合适的方法求该方程的解．

查看试题解析
20. 在某市2016年“书香校园，经典诵读”比赛活动中，有32万名学生参加比赛活动，其中有8万名学生分别获得一、二、三等奖，从获奖学生中随机抽取部分，绘制成不完整的统计表（如表），请根据图表解答下列问题．
获奖等级
频数
一等奖
a
二等奖
b
三等奖
275

(1)、表格中a的值为， b的值为．

(2)、扇形统计图中表示获得一等奖的扇形的圆心角为度．

(3)、估计全市有多少名学生获得三等奖？

查看试题解析
21. A、B、C、D、E五位同学进行一次乒乓球单打比赛，要从中选出两位同学打第一场比赛．

(1)、若已确定A打第一场，再从其余四位同学中随机选取一位，求恰好选中B同学的概率；

(2)、请用画树状图或列表法，求恰好选中A、B两位同学的概率．

查看试题解析
22. 在四边形ABCD中，AD∥BC，点E在BC边的延长线上，CE=BC，连接AE，交CD边于点F，且CF=DF．

(1)、如图1，求证：AD=BC；

(2)、如图2，连接BD、DE，若BD⊥DE，请判定四边形ABCD的形状，并证明．

查看试题解析
23. 如图1是安装在斜屋面上的热水器，图2是安装该热水器的侧面示意图．已知，斜屋面的倾角为25°，长为2.1米的真空管AB与水平线AD的夹角为40°，安装热水器的铁架水平横管BC长0.2米，求铁架垂直管CE的长（结果精确到0.01米）．

查看试题解析
24. 如图，AB为⊙O的直径，BC、AD是⊙O的切线，切点分别为B、A，过点O作EC⊥OD，EC交BC于点C，交AD于点E．

(1)、求证：CE是⊙O的切线；

(2)、若AE=1，AD=3，求阴影部分的面积．（结果保留π）

查看试题解析
25. 快、慢两车分别从相距180千米的甲、乙两地同时出发，沿同一路线匀速行驶，相向而行，快车到达乙地停留一段时间后，按原路原速返回甲地．慢车到达甲地比快车到达甲地早 $\frac{1}{2}$ 小时，慢车速度是快车速度的一半，快、慢两车到达甲地后停止行驶，两车距各自出发地的路程y（千米）与所用时间x（小时）的函数图象如图所示，请结合图象信息解答下列问题：

(1)、请直接写出快、慢两车的速度；

(2)、求快车返回过程中y（千米）与x（小时）的函数关系式；

(3)、两车出发后经过多长时间相距90千米的路程？直接写出答案．

查看试题解析
26.
如图①，在正方形ABCD中，对角线AC、BD交于点O，动点P在线段BC上（不含点B），∠BPE= $\frac{1}{2}$ ∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．

(1)、如图②，当点P与点C重合时，求证：△BOG≌△POE；

(2)、通过观察、测量、猜想： $\frac{B F}{P E}$ = ，并结合图①证明你的猜想；

(3)、把正方形ABCD改为菱形，其他条件不变（如图②），若∠ACB=a，直接写出 $\frac{B F}{P E}$ 的值，为．（用含a的式子表示）

查看试题解析
27.
已知：如图，抛物线y=ax²+bx﹣3与x轴交于A、B两点，与y轴交于点C，O是坐标原点，已知点B的坐标是（3，0），tan∠OAC=3；

(1)、求该抛物线的函数表达式；

(2)、点P在x轴上方的抛物线上，且∠PAB=∠CAB，求点P的坐标；

(3)、若平行于x轴的直线与抛物线交于点M、N（M点在N点左侧），
①若以MN为直径的圆与x轴相切，求该圆的半径；
②若Q（m，4）是直线MN上一动点，当以点C、B、Q为顶点的三角形的面积等于6时，请直接写出符合条件的m值，为．

查看试题解析

获奖等级	频数
一等奖	a
二等奖	b
三等奖	275