2016-2017学年江苏省徐州市睢宁县九年级下学期期中数学试卷

试卷更新日期：2017-05-25 类型：期中考试

进入出卷网下载

一、单选题

1. m²的算术平方根一定是（）

A、m B、﹣m C、|m| D、 $\sqrt{m}$

查看试题解析
2. 下列计算正确的是（）

A、4x﹣x=3 B、（3x²）³=9x⁶ C、（x+2）（x﹣2）=x²﹣4 D、 $\sqrt{6}$ ÷ $\sqrt{3}$ =2

查看试题解析
3. 2016年我省克服连续降雨等自然灾害影响，全年粮食总产达693.2亿斤，将693.2亿用科学记数法表示为（）

A、6.932×10¹⁰ B、693.2×10⁸ C、69.32×10⁹ D、69.32×10⁷

查看试题解析
4. 下列事件：①在干燥的环境中，种子会发芽；②在排球比赛中弱队战胜强队；③抛掷10枚硬币，5枚正面向上；④彩票的中奖概率是8%，买100张有8张会中奖，其中随机事件有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
5. 在下列四个图案中，既是轴对称图形，又是中心对称图形是（）

A、 B、 C、 D、

查看试题解析
6. △ABC是⊙O的内接三角形，⊙O的直径为10，∠ABC=45°，则AC的长是（）

A、5 B、10 C、5 $\sqrt{2}$ D、10 $\sqrt{2}$

查看试题解析
7. 一次函数y=﹣ $\frac{3}{2}$ x﹣1的图象不经过的象限是（）

A、第四象限 B、第三象限 C、第二象限 D、第一象限

查看试题解析
8. 如图，点M是抛物线y=ax²（x＞0）上的任意一点，MA⊥x轴于点A，MB⊥y轴于点B，连接AB，交抛物线于点P，则 $\frac{P A}{P B}$ 的值是（）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} + 1}{2}$ C、 $\frac{3 - \sqrt{5}}{2}$ D、 $\frac{3 + \sqrt{5}}{2}$

查看试题解析

二、填空题

9. 绝对值是5的有理数是．

查看试题解析
10. 点P（3，﹣4）到坐标原点的距离为．

查看试题解析
11. 函数y= $\frac{1}{\sqrt{x - 1}}$ 中，自变量x的取值范围是．

查看试题解析
12. 若x²﹣2x﹣3=0，则代数式2x²﹣4x的值为．

查看试题解析
13. 已知圆锥的底面直径为4，母线长为6，则它的侧面展开图的圆心角为度．

查看试题解析
14. 在某一时刻，测得一根高为1.8m的竹竿的影长为3m，同时测得一根旗杆的影长为25m，那么这根旗杆的高度为m．

查看试题解析
15. 小明从P点出发，沿直线前进10米后向右转a，接着沿直线前进10米，再向右转a，…，照这样走下去，第一次回到出发地点P时，一共走了120米，则a的度数是．

查看试题解析
16. 在矩形ABCD中，AB=6，AD=10，点E是边BC的中点，连接AE，若将△ABE沿AE翻折，点B落在点F处，连接FC，则tan∠BCF= ．

查看试题解析
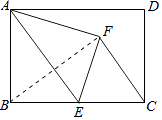17. 已知关于x的一元二次方程x²+ax﹣（m﹣1）（m+2）=0，对于任意实数a都有实数根，则m的取值范围是．

查看试题解析
18. 如图，在△ABC中，AB=AC=6，∠BAC=120°，点D是AB边上的点， $\frac{A D}{D B}$ = $\frac{1}{2}$ ，点P为底边BC上的一动点，则△PDA周长的最小值为．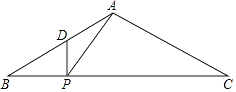

查看试题解析

三、解答题

19. 计算：

(1)、|1﹣ $\sqrt{3}$ |+（﹣1）²⁰¹⁷﹣（3﹣π）⁰

(2)、（1﹣ $\frac{1}{x - 1}$ ）÷ $\frac{x - 2}{x - x^{2}}$ ．

查看试题解析
20. 计算题

(1)、解方程组 ${\begin{cases} - x + 3 y = 7 \\ 2 x = 5 y \end{cases}$ ；

(2)、解不等式： $\frac{x + 4}{2}$ ＜4﹣ $\frac{2 x - 1}{3}$ ，并把解集在数轴上表示出来．

查看试题解析
21. 学校为了解学生“自主学习、合作交流”的情况，对八年级各班部分同学进行了一段时间的跟踪调査，将调查结果（A：特别好；　B：较好；　C：一般；　D：较差）绘制成以下两幅不完整的统计图．
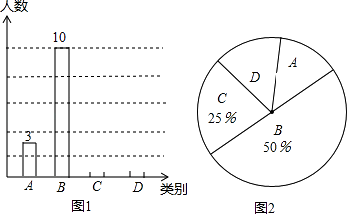
请根据图中提供的信息，解答下列问题：

(1)、此次跟踪调查的学生有人；扇形统计图中，D类所占圆心角为度；

(2)、补全条形统计图；

(3)、如果该校八年级共有学生360人，试估计A类学生大约有多少人？

查看试题解析
22. 6月5日是“世界环境日”，某校从3名男生和2名女生中随机抽取学生去参加市中学生环保演讲比赛．

(1)、若抽取1名学生参加，恰好是男生的概率是；

(2)、如果抽取1名学生参加，请用列表或树状图求出恰好是1名男生和1名女生的概率．

查看试题解析
23. 从南京到某市可乘坐普通列车，行驶路程是520千米；也可乘坐高铁，行驶路程是400千米．已知高铁的平均速度是普通列车平均速度的2.5倍，且从南京到该市乘坐高铁比乘坐普通列车要少用3小时．求高铁行驶的平均速度．

查看试题解析
24.
高铁给我们的出行带来了极大的方便．如图，“和谐号”高铁列车座椅后面的小桌板收起时，小桌板的支架的底端N与桌面顶端M的距离MN=75cm，且可以看作与地面垂直．展开小桌板使桌面保持水平，AB⊥MN，∠MAB=∠MNB=37°，且支架长BN与桌面宽AB的长度之和等于MN的长度．求小桌板桌面的宽度AB（结果精确到1cm，参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

查看试题解析
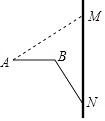25. 如图，AB是⊙O的弦，点C在⊙O外，OC⊥OA，并交AB于点P，且CP=CB．

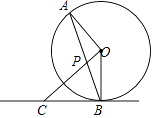(1)、判断CB与⊙O的位置关系，并说明理由；

(2)、若⊙O的半径为3，OP=1，求弦AB的长．

查看试题解析
26. 如图，矩形ABCD中，AD=5，AB=8，点E为射线DC上的一个动点，把△ADE沿AE折叠点．D的对应点为D′．

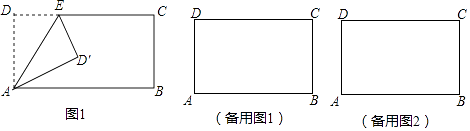(1)、求点D′刚好落在对角线AC上时，D′C的长；

(2)、求点D′刚好落在此对称轴上时，线段DE的长．

查看试题解析
27. 甲乙两台智能机器人从同一地点P出发，沿着笔直的路线行走了450cm到点Q．甲比乙先出发，乙出发一段时间后速度提高为原来的2倍．甲匀速走完全程．两机器人行走的路程y（cm）与时间x（s）之间的函数图象如图所示．根据图象所提供的信息解答下列问题：

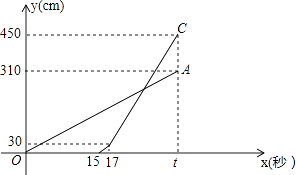(1)、乙比甲晚出发秒，乙提速前的速度是每秒cm，t=；

(2)、当x为何值时，乙追上了甲？

(3)、若两台机器人到达终点Q后迅速折返，并保持折返前的速度继续匀速行走返回到点P，乙比甲早到多长时间？

查看试题解析
28.
如图，抛物线y₁=﹣ax²+2ax﹣a﹣3（a＞0）和y₂=a（x+1）²﹣1（a＞0）的顶点分别为M、N，与y轴分别交于E、F．

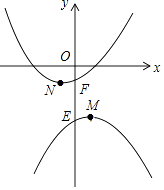(1)、①函数y₁=﹣ax²+2ax﹣a﹣3（a＞0）的最大值是；
②当y₁、y₂的值都随x的增大而增大时，自变量x的取值范围是；

(2)、当EF=MN时，求a值，并判断四边形EMFN是何种特殊的四边形；

(3)、若y₂=a（x+1）²﹣1（a＞0）的图象与x轴的右交点为A（m，0），当△AMN为等腰三角形时，求方程a（x+1）²﹣1=0的解．

查看试题解析