人教版2018-2019学年九年级下学期数学期末模拟卷
试卷更新日期:2019-06-04 类型:期末考试
一、选择题
-
1. 由6个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 2.
2.如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB∶FG=2∶3,则下列结论正确的是( )
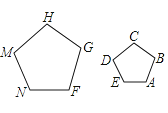 A、2DE=3MN B、3DE=2MN C、3∠A=2∠F D、2∠A=3∠F3. 在△ABC中,∠C=90°,∠B=50°,AB=10,则BC的长为( )
A、2DE=3MN B、3DE=2MN C、3∠A=2∠F D、2∠A=3∠F3. 在△ABC中,∠C=90°,∠B=50°,AB=10,则BC的长为( )
A、10tan50° B、10sin40° C、10sin50° D、4. 今年“父亲节”佳佳给父亲送了一个礼盒,该礼盒的主视图是( )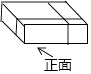 A、
A、 B、
B、 C、
C、 D、
D、 5. 对于反比例函数 , 下列说法正确的是( )A、图象经过点(2,﹣1) B、图象位于第二、四象限 C、当x<0时,y随x的增大而减小 D、当x>0时,y随x的增大而增大6. 在△ABC中,∠C=90°,AC=1,BC=2,则 cos A的值是( )A、 B、 C、 D、7.
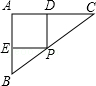
5. 对于反比例函数 , 下列说法正确的是( )A、图象经过点(2,﹣1) B、图象位于第二、四象限 C、当x<0时,y随x的增大而减小 D、当x>0时,y随x的增大而增大6. 在△ABC中,∠C=90°,AC=1,BC=2,则 cos A的值是( )A、 B、 C、 D、7.如图,Rt△ABC中,AB⊥AC,AB=3,AC=4,P是BC边上一点,作PE⊥AB于E,PD⊥AC于D,设BP=x,则PD+PE=( )
 A、 B、 C、 D、8. 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )
A、 B、 C、 D、8. 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )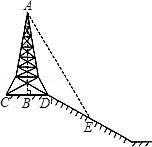 A、24m B、22m C、20m D、18m9. 如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )
A、24m B、22m C、20m D、18m9. 如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=α,则cosα的值为( )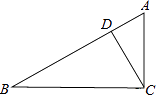 A、 B、 C、 D、10. 如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=﹣ 、y= 的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
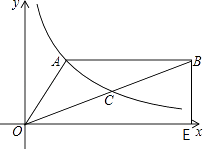
A、 B、 C、 D、10. 如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=﹣ 、y= 的图象交于B、A两点,则∠OAB的大小的变化趋势为( )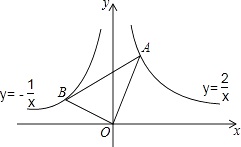 A、逐渐变小 B、逐渐变大 C、时大时小 D、保持不变11. 如图,点A是反比例函数y=(x>0)的图象上的一点,且点A的横坐标为2,连接OA并延长到点B,使AB=OA,过点B作x轴和y轴的垂线,垂足分别为C,D,则图中阴影部分的面积为( )
A、逐渐变小 B、逐渐变大 C、时大时小 D、保持不变11. 如图,点A是反比例函数y=(x>0)的图象上的一点,且点A的横坐标为2,连接OA并延长到点B,使AB=OA,过点B作x轴和y轴的垂线,垂足分别为C,D,则图中阴影部分的面积为( )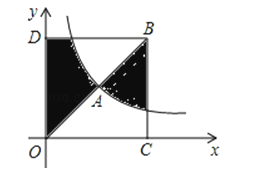 A、23 B、18 C、11 D、812. 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为 , 则下列结论中正确的是( )
A、23 B、18 C、11 D、812. 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为 , 则下列结论中正确的是( ) A、m=5 B、m=4 C、m=3 D、m=10
A、m=5 B、m=4 C、m=3 D、m=10二、填空题
-
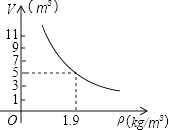
13. 一定质量的二氧化碳,其体积V(m3)是密度ρ(kg/m3)的反比例函数,请你根据图中的已知条件,写出反比例函数的关系式,当V=1.9m3时,ρ= .
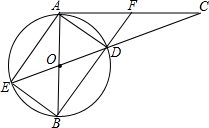
 14. CD为⊙O的直径,弦AB⊥CD于点E,CD=10,AB=8,则tan∠DAE= .15. 在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为m.16.
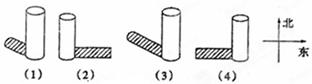
14. CD为⊙O的直径,弦AB⊥CD于点E,CD=10,AB=8,则tan∠DAE= .15. 在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为m.16.如图所示是小红在某天四个时刻看到一个棒及其影子的情况,那么她看到的先后顺序是 .
 17. 将△ABC的纸片按如图所示的方式折叠,使点B落在边AC上,记为点B′,折叠痕为EF,已知AB=AC=8,BC=10,若以点B′、F、C为顶点的三角形与△ABC相似,那么BF的长度是 .
17. 将△ABC的纸片按如图所示的方式折叠,使点B落在边AC上,记为点B′,折叠痕为EF,已知AB=AC=8,BC=10,若以点B′、F、C为顶点的三角形与△ABC相似,那么BF的长度是 .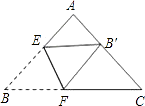 18. 函数y=x的图象与函数y= 的图象在第一象限内交于点B,点C是函数y= 在第一象限图象上的一个动点,当△OBC的面积为3时,点C的横坐标是 .
18. 函数y=x的图象与函数y= 的图象在第一象限内交于点B,点C是函数y= 在第一象限图象上的一个动点,当△OBC的面积为3时,点C的横坐标是 .
三、解答题
-
19. 计算:cos245°+ ﹣ •tan30°.20. 如图是由几个小立方体搭成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,请你画出这个几何体的主视图和左视图.
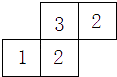 21. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且 .
21. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且 .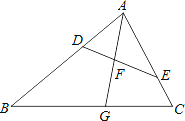 (1)、求证:△ADF∽△ACG;(2)、若 ,求 的值.22. 数学实践活动小组借助载有测角仪的无人机测量象山岚光阁与文明湖湖心亭之间的距离.如图,无人机所在位置P与岚光阁阁顶A、湖心亭B在同一铅垂面内,P与B的垂直距离为300米,A与B的垂直距离为150米,在P处测得A、B两点的俯角分别为α、β,且tanα= ,tanβ= ﹣1,试求岚光阁与湖心亭之间的距离AB.(计算结果若含有根号,请保留根号)
(1)、求证:△ADF∽△ACG;(2)、若 ,求 的值.22. 数学实践活动小组借助载有测角仪的无人机测量象山岚光阁与文明湖湖心亭之间的距离.如图,无人机所在位置P与岚光阁阁顶A、湖心亭B在同一铅垂面内,P与B的垂直距离为300米,A与B的垂直距离为150米,在P处测得A、B两点的俯角分别为α、β,且tanα= ,tanβ= ﹣1,试求岚光阁与湖心亭之间的距离AB.(计算结果若含有根号,请保留根号)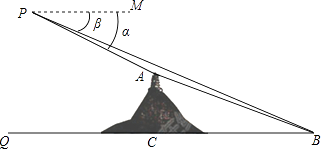 23. 如图,在△ABC中,∠C=90°,点D、E分别在AC、AB上,BD平分∠ABC,DE⊥AB,AE=6,cos A= .求:
23. 如图,在△ABC中,∠C=90°,点D、E分别在AC、AB上,BD平分∠ABC,DE⊥AB,AE=6,cos A= .求: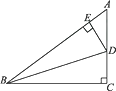 (1)、DE、CD的长;
(1)、DE、CD的长;
(2)、tan∠DBC的值.
24. 如图所示,a是海面上一条南北方向的海防警戒线,在a上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处,某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号,在当时气象条件下,声波在水中的传播速度是1.5 km/s.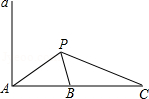 (1)、设A到P的距离为xkm,用x表示B,C到P的距离,并求x值;(2)、求静止目标P到海防警戒线a的距离(结果精确到0.01 km).
(1)、设A到P的距离为xkm,用x表示B,C到P的距离,并求x值;(2)、求静止目标P到海防警戒线a的距离(结果精确到0.01 km).