山东省泰安市泰山区2018-2019学年中考数学二模考试试卷

试卷更新日期：2019-06-04 类型：中考模拟

进入出卷网下载

一、选择题（本大题共12个小题，每小题选对4分）

1. 下列实数中，最大的数是（）

A、-|-4| B、0 C、1 D、-（-3）

查看试题解析
2. 2018年国庆小长假，奉安市旅游再次交出漂亮“成绩单”，全市纳入重点监测的21个旅游景区、旅游大项目、乡村旅游点实现旅游收入近1320000元，将1320000用科学记数法表示为（）

A、1.32×10⁹ B、1.32×10⁸ C、1.32×10⁷ D、1.32×10⁶

查看试题解析
3. 下列运算正确的是（）

A、a³.a⁴=¹² B、a⁵÷a-³=a² C、(3a⁴)²=6a⁸ D、(-a)⁵.a=-a⁶

查看试题解析
4. 下列四个图形中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 如图，直线a∥b，直线c分别交a，b于点.C.∠BAC的平分线交直线b于点D，若∠2=50°，则∠1的度数是（）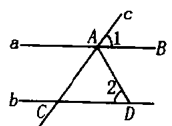

A、50° B、60° C、80° D、100°

查看试题解析
6. 某校对部分参加研学旅行社会实践活动的中学生的年龄（单位；岁)进行统计，结果如下表：

年龄

12

12

14

15

16

人数

1

2

2

3

1

则这些学生年龄的众数和中位数分别是（）

A、15，14 B、15,13 C、14，14 D、13.14

查看试题解析
7. 如图，点B、C、D在⊙O上，若∠BCD=140°，则∠BOD的度数是（）

A、40° B、50° C、80° D、90°

查看试题解析
8. 已知关于x的一元二次方程x²-2kx+6=0有两个相等的实数根，则k的值为（）

A、±2 $\sqrt{6}$ /6 B、± $\sqrt{6}$ C、2或3 D、 $\sqrt{6}$ 或 $\sqrt{3}$

查看试题解析
9. 给出下列函数:①y=2x-3；②y= $\frac{1}{x}$ ；③y=2x²；④y=-3x+1.上述函数中符合条件“当x>0时，函数值y随自变量x增大而增小”的是（）

A、①③ B、③④ C、②④ D、②③

查看试题解析
10. 如图，在菱形ABCD中，∠A=60°，4D=4，点F是AB的中点，过点F作FE⊥AD，垂足为E，将△AEF沿点A到点B的方向平移，得到△A'E’F'，设点P、P’分别是EF、E'F'的中点，当点A’与点B重合时，四边形PP’CD的面积为（）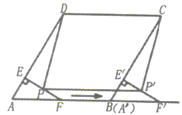

A、7 $\sqrt{3}$ B、6 $\sqrt{3}$ C、8 $\sqrt{3}$ D、8 $\sqrt{3}$ -4

查看试题解析
11. 如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF相交于点给出下列结论：①BE=2AE；②△DFP∽△BPA：③ $\frac{P F}{P H} = \frac{3}{5}$ ：④DP²=PH.PC其中正确的是（）

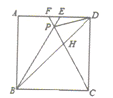A、①②③④ B、①③④ C、②③ D、①②④

查看试题解析
12. 二次函数y=ax²+br+c(a≠0)的图象如图所示，给出下列四个结论：①abc >0；②3b+2c<0；③4a+c<2b；④当y>0时，- $\frac{5}{2}$ <x< $\frac{1}{2}$ ，其中结论正确的个数是（）

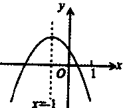A、2 B、3 C、4 D、1

查看试题解析

二、填空题（本大题共6小题，满分24分.每小题填对得4分）

13. 不等式组 ${\begin{cases} \frac{x - 1}{2} + 2 > x \\ 2 (x - 2) \leq 3 x - 5 \end{cases}$ 的解集是 .

查看试题解析
14. 为迎接文明城市的验收工作，某居委会组织两个检查组，分别对“垃圾分类”和“违规停车”的情况进行抽查。各组随机抽取辖区内某三个小区中的一个进行检查，则两个组恰好抽到同一个小区的概率是.

查看试题解析
15. 如图是某圆锥的主视图和左视图，则该圆锥的表面积是.

查看试题解析
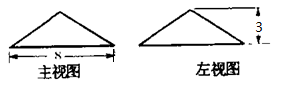16. 如图，一艘海轮位于灯塔P的南偏东45°方向，距离灯塔400海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的北偏东30°方向上的B处，这时B处与灯塔P的距离为海里

查看试题解析
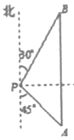17. 如图，在矩形ABCD中，对角线AC、BD交于点O，过点A作EA⊥CA交DB的延长线于点E，若AB=3，BC=4，则 $\frac{A O}{A E}$ 的值为 .

查看试题解析
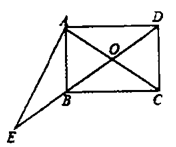18. 如图，四条直线l₁：y₁= $\frac{\sqrt{3}}{3}$ x，l₂：y₂= $\sqrt{3}$ x，l₃：y₃=- $\sqrt{3}$ x，l₄：y₄=- $\frac{\sqrt{3}}{3}$ x，OA₁=1，过点A₁作A₁A₂⊥x轴交l₁于点A₂ ，再过点A₂作A₂A₃⊥l₁ ，交l₂于点A₃ ，再过点A₃作A₃A₄⊥l₂交y轴于点A₄.…，则点A₂₀₂₀的坐标为.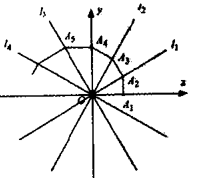

查看试题解析

三、解答题（本大题共7小题，满分78分.）

19. 先化简，再求值: $(a - 1 - \frac{2 a - 1}{a + 1}) \div \frac{a^{2} - 4 a + 4}{a + 1}$ ,其中a=2+ $\sqrt{3}$ .

查看试题解析
20. 民俗村的开发和建设，带动了旅游业的发展，某市有A、B、C、D、E五个民俗旅游村及“其它”景点，该市旅游部门绘制了2018年“五·一”长假期间民俗村旅游情况统计图如下：
某市2018年“五.一”长假期间民俗旅游情况统计图

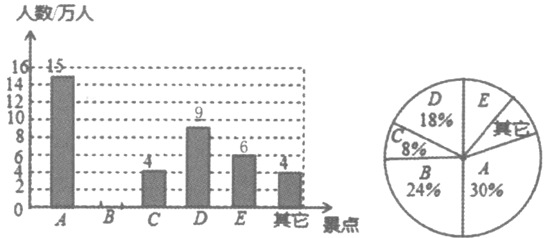
根据以上信息解答：

(1)、2018年“五·一”期间，该市五个旅游村及“其它”景点共接待游客万人，扇形统计图中D民俗村所对应的圆心角的度数是，并补全条形统计图；

(2)、根据近几年到该市旅游人数增长趋势，预计2019年“五·一”节将有70万游客选择该市旅游，请估计有多少万人会选择去E民俗村旅游?

(3)、甲、乙两个旅行团在A、C、D三个民俗村中，同时选择去同一个民俗村的概率是多少？请用画树状图或列表法加以说明.

查看试题解析
21. 如图，一次函数y=x+b与反比例函数y= $\frac{m}{x}$ 的图象交于A（2，3），B(-3，n)两点。

(1)、求一次函数与反比例函数的表达式；

(2)、过点B作BC⊥x轴，垂足为C，连接AC，求△ABC的面积

查看试题解析
22. 如图，四边形ABCD中，AC⊥BD交BD于点E，点F、M分别是AB、BC的中点，BN平分∠ABE交AM于点N，AB=AC=BD，连接MF、NF.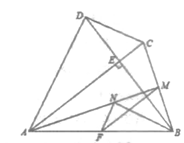

(1)、判断△BMN的形状，并证明你的结论；

(2)、求证：△MFN∽△BDC.

查看试题解析
23. 甲、乙两个工程队计划修建一条长18千米的乡村公路，已知甲工程队比乙工程队每天多修路0.6千米，乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍。

(1)、求甲、乙两个工程队每天各修路多少千米?

(2)、若甲工程队每天的修路费用为0.6万元，乙工程队每天的修路费用为0.5万元，要使两个工程队修路总费用不超过6.3万元，甲工程队至少修路多少天？

查看试题解析
24. 如图1，在平面直角坐标系中，已知抛物线y=ax²+bx-5与x轴交于点A（-1，0），B(5，0)两点，与y轴交于点C.

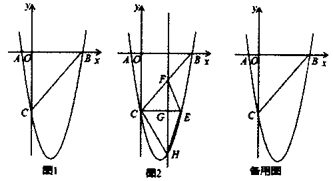(1)、求抛物线的函数表达式；

(2)、如图2，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC、CE分别相交于点F、G，试探究当点日运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积；

(3)、若点K为抛物线的顶点，点M(4，m)是该抛物线上的一点，在x轴、y轴上分别找点P、Q，使四边形PQKM的周长最小，请直接写出符合条件的点P、Q的坐标.

查看试题解析
25. 如图，在△ABC中，∠BAC=90°，AB=AC，点E在AC上（且不与点A、C重合）.在△ABC的外部作△CED，使∠CED=90°，DE=CE，连接AD，分别以AB、AD为邻边作平行四边形ABFD，连接AF.

(1)、根据图①写出线段AF、AE之间存在的等量关系式，并给予证明；

(2)、将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请直接
写出线段AF、AE的数量关系；

(3)、在图②基础上，将△CED绕点C继续逆时针旋转，请判断（2）间中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，说明理由.

查看试题解析

年龄	12	12	14	15	16
人数	1	2	2	3	1