山东省德州市宁津县2018-2019学年中考数学二模考试试卷

试卷更新日期：2019-06-04 类型：中考模拟

进入出卷网下载

一、选择题：本大题共12小题，每小题选对得4分，

1. 9的平方根是（　　）

A、3 B、-3 C、±3 D、81

查看试题解析
2. 下列图形中，是轴对称图形，但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算，正确的是（）

A、a²·a²=2a² B、3 $\sqrt{a}$ - $\sqrt{a}$ =3 C、(-a²)²=a⁴ D、(a+1)²=a2+1

查看试题解析
4. 空气中有一种有害粉尘颗粒，其直径大约为0.000000017m，该直径可用科学记数法表示为（）

A、0.17×10^-7m B、1.7×10⁷m C、1.7×10^-8m D、1.7x10⁸m

查看试题解析
5. 如图是由一个圆柱体和一个长方体组成的几何体，其左视图是（）

A、 B、 C、 D、

查看试题解析
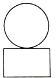6. 下列各数：-2，0， $\frac{1}{3}$ ，0.020020002…， $π$ ， $\sqrt{9}$ ，其中无理数的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
7. 如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=6，AB=20，则△ABD的面积是（）

A、30 B、45 C、60 D、90

查看试题解析
8. 如图，四边形ABCD内接于⊙O，AB经过圆心，∠B=3∠BAC，则∠ADC等于（）

A、100° B、112.5° C、120° D、135°

查看试题解析
9. 如图，在矩形ABCD中，点P从点A出发，沿着矩形的边顺时针方向运动一周回到点A，则点A、P、D围成的图形面积y与点P运动路程x之间形成的函数关系式的大致图象是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在 $▱$ ABCD中，AC，BD相交于点O，点E是OA的中点，连接BE并延长交AD于点F，已知S_△AEF=4，则下列结论：① $\frac{A F}{F D} = \frac{1}{2}$ ：②S_△BCE=36：③S_△ABE=12：④△AEF∽△ACD；其中一定正确的是（）

A、①②③④ B、①④ C、②③④ D、①②③

查看试题解析
11. 如图，直线y= $\frac{2}{3}$ x+4与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（）

A、(-3，0) B、(-6，0) C、(- $\frac{3}{2}$ ，0) D、(- $\frac{5}{2}$ ，0）

查看试题解析
12. 已知二次函数y=-x²+x+6及一次函数y=-x+m，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新函数（如图所示），当直线y=-x+m与新图象有4个交点时，m的取值范围是（）

A、- $\frac{25}{4}$ <m<3 B、- $\frac{25}{4}$ <m<-2 C、-2<m<3 D、-6<m<-2

查看试题解析

二、填空题：本大题共6小题，共24分，每小题填对得4分.

13. 如图，直线a∥b，∠1=140°，则∠2=。

查看试题解析
14. 已知一组数据1，2，0，-1，x，1的平均数是1，那么这组数据的方差是.

查看试题解析
15. 一般地，当a，β为任意角时，sin(a+β)与sin(a-β)的值可以用下面的公式求得：
sin(a+β)=sina·cosβ+cosa·sinβ:sin(a-β)=sina·cosβ-cosa·sinβ.例如sin90°=sin(60°+30°）=sin60°·cos30°+cos60°·sin30°= $\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2} + \frac{1}{2} \times \frac{1}{2}$ =1,类似地，可以求得sin15°的值是 .

查看试题解析
16. 如图，圆锥的底面直径是10cm，高为12cm，则它的侧面展开图的面积是cm²。

查看试题解析
17. 若关于x的分式方程 $\frac{2 x - a}{x - 2} = \frac{1}{2}$ 的解为正数，则a的取值范围是。

查看试题解析
18. 观察下列各式
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1 \times 2}$ ； $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2 \times 3}$ ； $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3 \times 4}$ ；….
请你利用你发现的规律，计算
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} + \sqrt{1 + \frac{1}{9^{2}} + \frac{1}{10^{2}}}$ 其结果为 .

查看试题解析

三、解答题：本大题共7小题，共78分.

19. 先化简，再求值：（x-1）÷ $(\frac{2}{x + 1} - 1)$ ，其中x为方程x²+3x+2=0的根.

查看试题解析
20. 2013年5月31日是第26个“世界无烟日”，校学生会书记小明同学就“戒烟方式”的了解程度对本校九年级学生进行了一次随机问卷调查，如图是他采集数据后绘制的两幅不完整的统计图（A：了解较多，B：不了解，C：了解一点，D：非常了解）.请你根据图中提供的信息解答以下问题：

(1)、在扇形统计图中的横线上填写缺失的数据，并把条形统计图补充完整。

(2)、2013年该初中九年级共有学生400人，按此调查，可以估计2013年该初中九年级学生中对戒烟方式“了解较多”以上的学生约有多少人？

(3)、在问卷调查中，选择“A”的是1名男生，1名女生，选择“D”的有4人且有2男2女.校学生会要从选择“A、D”的问卷中，分别抽一名学生参加活动，请你用列表法或树状图求出恰好是一名男生一名女生的概率。

查看试题解析
21. 数学活动课，老师和同学一起去测量校内某处的大树AB的高度，如图，老师测得大树前斜坡DE的坡度i=1：4，一学生站在离斜坡顶端E的水平距离DF为8m处的D点，测得大树顶端A的仰角为30°，已知BE=2m，此学生身高CD=1.7m，求大树的高度AB的值.（结果保留根号）

查看试题解析

22. 绿色无公害蔬菜基地有甲、乙两种植户，他们种植了A，B两类蔬菜，两种植户种植的两类蔬菜的种植面积与总收入如下表：

种植户	种植A类蔬菜面积（单位：面）	种植B类蔬菜面积（单位：面）	总收入（单位：元）
甲	3	1	12500
乙	2	3	16500

说明：不同种植户种植的同类蔬菜每亩的平均收入相等；亩为土地面积单位.

(1)、求A、B两类蔬菜每亩的平均收入各是多少元；

(2)、某种植户准备租20亩地用来种植A、B两类蔬菜，为了使总收入不低于63000元，且种植A类蔬菜的面积多于种植B类蔬菜的面积（两类蔬菜的种植面积均为整数），求该种植户所有租地方案；

(3)、在（2）的基础上，指出哪种方案使总收入最大，并求出最大值.

查看试题解析

23. 已知：如图，以等边△ABC的边BC为直径作⊙O，分别交AB，AC于点D，E，过点D作DF⊥AC交AC于点F.

(1)、求证：DF是⊙O的切线；

(2)、若等边△ABC的边长为8，求由 $\overset{⌢}{D E}$ 、DF、EF围成的阴影部分面积

查看试题解析
24. 如图1，在正方形ABCD中，E、F分别是BC，CD上的点，且∠EAF=45°.则有结论EF=BE+FD成立；

(1)、如图2，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是BC，CD上的点，且∠EAF是∠BAD的一半，那么结论EF=BE+FD是否仍然成立？若成立，请证明；不成立，请说明理由.

(2)、若将（1）中的条件改为：如图3，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，延长BC到点E，延长CD到点F，使得∠EAF仍然是∠BAD的一半，则结论EF=BE+FD是否仍然成立？若成立，请证明；不成立，请写出它们的数量关系并证明.

查看试题解析
25. 如图1，已知二次函数y=ax²+bx+c(a、b、c为常数，a≠0)的图象过点O（0，0）和点A（4，0），函数图象最低点M的纵坐标为- $\frac{8}{3}$ ，直线l的解析式为y=x.

(1)、求二次函数的解析式；

(2)、直线/沿x轴向右平移，得直线I，I与线段0A相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线/折叠，当点E恰好落在抛物线上点E'时（图2），求直线l的解析式；

(3)、在（2）的条件下，I与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B’ON'，
P为l上的动点，当△PB’N'为等腰三角形时，求符合条件的点P的坐标.

查看试题解析