河北省张家口市桥东区2018-2019学年中考数学一模考试试卷
试卷更新日期:2019-06-04 类型:中考模拟
一、选择题(本大题共16个小题,共42分.1~10小题各3分,11~16小题各2分.)
-
1. 下列图形中不具有稳定性的是( )A、
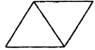 B、
B、 C、
C、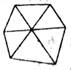 D、
D、 2. 斑叶兰被列为国家二级保护植物,它的一粒种子重约0.0000005克.将0.0000005用科学记数法表示为( )A、5×107 B、5×10-7 C、0.5×10-6 D、5×10-63. 以四种不同的方式连接正六边形的两条对角线,连接后的情形如下列选项中的图形所示,则下列哪一个图形不是轴对称图形( )A、
2. 斑叶兰被列为国家二级保护植物,它的一粒种子重约0.0000005克.将0.0000005用科学记数法表示为( )A、5×107 B、5×10-7 C、0.5×10-6 D、5×10-63. 以四种不同的方式连接正六边形的两条对角线,连接后的情形如下列选项中的图形所示,则下列哪一个图形不是轴对称图形( )A、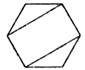 B、
B、 C、
C、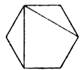 D、
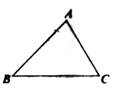
D、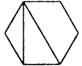 4. 计算-42的结果等于( )A、-8 B、-16 C、8 D、165. 如图,锐角三角形ABC中,BC>AB>AC,甲、乙两人想找一点P,使得∠BPC与∠A互补,其作法分别如下:
4. 计算-42的结果等于( )A、-8 B、-16 C、8 D、165. 如图,锐角三角形ABC中,BC>AB>AC,甲、乙两人想找一点P,使得∠BPC与∠A互补,其作法分别如下:(甲)以A为圆心,AC长为半径画弧交AB于P点,则P即为所求;
(乙)作过B点且与AB垂直的直线l,作过C点且与AC垂直的直线,交l于P点,则P即为所求.
对于甲、乙两人的作法,下列叙述正确的是( )
 A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确6. 下列关于a、b的等式,有一个是错误的,其它都是正确的,则错误的是( )A、b=3a B、b-a=0 C、b2-9a2=0 D、2b+m=6a+m7. 下列说法中,正确的是( )A、(-3)2是负数 B、最小的有理数是零 C、若|x|=5,则x=5或-5 D、任何有理数的绝对值都是正数8. 如图为一直棱柱,其底面是三边长为5、12、13的直角三角形。若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为( )A、
A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确6. 下列关于a、b的等式,有一个是错误的,其它都是正确的,则错误的是( )A、b=3a B、b-a=0 C、b2-9a2=0 D、2b+m=6a+m7. 下列说法中,正确的是( )A、(-3)2是负数 B、最小的有理数是零 C、若|x|=5,则x=5或-5 D、任何有理数的绝对值都是正数8. 如图为一直棱柱,其底面是三边长为5、12、13的直角三角形。若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为( )A、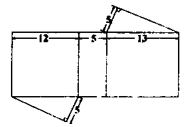 B、
B、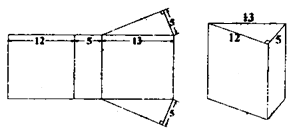 C、
C、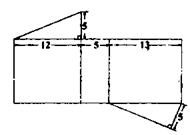 D、
D、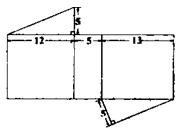 9. 2022年将在北京一张家口举办冬季奥运会,很多学校为此开设了相关的课程。下表记录了某校4名同学短道速滑成绩的平均数 和方差S2 , 根据表中数据,要选一名成绩好又发挥稳定的运动员参加比赛,应选择( )
9. 2022年将在北京一张家口举办冬季奥运会,很多学校为此开设了相关的课程。下表记录了某校4名同学短道速滑成绩的平均数 和方差S2 , 根据表中数据,要选一名成绩好又发挥稳定的运动员参加比赛,应选择( )队员1
队员2
队员3
队员4
平均数
51
50
51
50
方差S2
3.5
3.5
7.5
8.5
A、队员1 B、队员2 C、队员3 D、队员410. 在等腰△ABC中,AB=AC,D、E分别是BC,AC的中点,点P是线段AD上的一个动点,当△PCE的周长最小时,P点的位置在△ABC的( ) A、重心 B、内心 C、外心 D、不能确定11. 如图,有A,B,C三个地点,且AB⊥BC,从A地测得B地在A地的北偏东43°的方向上,那么从B地测得C地在B地的( )
A、重心 B、内心 C、外心 D、不能确定11. 如图,有A,B,C三个地点,且AB⊥BC,从A地测得B地在A地的北偏东43°的方向上,那么从B地测得C地在B地的( )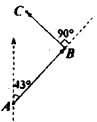 A、北偏西43° B、北偏西90° C、北偏东47° D、北偏西47°12. 半径为R、r的两个同心圆如图所示,已知半径为r的圆周长为a,且R-r=1,则半径为R的圆周长为( )
A、北偏西43° B、北偏西90° C、北偏东47° D、北偏西47°12. 半径为R、r的两个同心圆如图所示,已知半径为r的圆周长为a,且R-r=1,则半径为R的圆周长为( )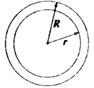 A、a+1 B、a+2 C、a+π D、a+2π13. 如图,设k= (a>b>0),则有( )
A、a+1 B、a+2 C、a+π D、a+2π13. 如图,设k= (a>b>0),则有( ) A、0<k< B、 <k<1 C、0<k<1 D、1<k<214. 如图,点E点为△ABC的内心,且EF⊥BC于点F,若∠BAC=38°,∠B=56°,则∠AEF的度数为( )
A、0<k< B、 <k<1 C、0<k<1 D、1<k<214. 如图,点E点为△ABC的内心,且EF⊥BC于点F,若∠BAC=38°,∠B=56°,则∠AEF的度数为( ) A、163 B、164 C、165 D、16615. 若x>1,y>0,且满足xy=xy , =x3y,则x+y的值为( )A、1 B、2 C、 D、16. 已知函数y1=a-x2(1≤x≤2)图象上某点P,其关于x轴的对称点在函数y2=x+1的图象上,则实数a的取值范围是( )A、A≥5 B、1≤a≤2 C、- ≤a≤1 D、-1≤a≤1
A、163 B、164 C、165 D、16615. 若x>1,y>0,且满足xy=xy , =x3y,则x+y的值为( )A、1 B、2 C、 D、16. 已知函数y1=a-x2(1≤x≤2)图象上某点P,其关于x轴的对称点在函数y2=x+1的图象上,则实数a的取值范围是( )A、A≥5 B、1≤a≤2 C、- ≤a≤1 D、-1≤a≤1二、填空题(本大题有3个小题,共12分.17~18小题各3分,19小题有3个空,每空2分.)
-
17. 已知a与b互为相反数,则代数式a2+2ab+b2+2019的值为 .18. 正方形的边长为a,它的面积与长为4cm、宽为12cm的长方形的面积相等,则a=cm.19. 如图,有一个圆O和两个正六边形T1 , T2.T1的6个顶点都在圆周上,T1的6条边都和圆O相切(我们称T1;T2分别为圆O的外切正六边形和内接正六边形).若设T1 , T2的周长分别为a,b,圆O的半径为r,则r:a= ;r:b=;正六边形T1 , T2 , 的面积比S1:S2 , 的值是.

三、解答题(本大题共7个小题,共66分.)
-
20. 已知:A、B都是关于x的多项式,A=3x2-5x+6,B=□-6,其中多项式B有一项被“□”遮挡住了(1)、当x=1时,A=B,请求出多项式B被“□”遮挡的这一项的系数;
(2)、若A+B是单项式,请直接写出多项式B.21. 某班老师要求每人每学期读4~7本书,并随机抽查了本学期学生读课外书册数的情况,绘制成不完整的条形图和不完整的扇形图,其中条形图被墨迹遮盖了一部分,回答下列问题: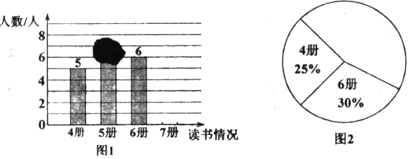 (1)、请你求出老师随机抽查了多少名学生;(2)、已知册数的中位数是5,
(1)、请你求出老师随机抽查了多少名学生;(2)、已知册数的中位数是5,嘉嘉说:条形图中被遮盖的数为5
淇淇说:条形图中被遮盖的数为6
i你认为嘉嘉和淇淇谁说的正确,请说明原因,并把条形图补充完整;
ii在扇形图中,“7册”部分所对的圆心角为 °,并把扇形图补充完整;
(3)、请直接写出:从抽查学生中任取两人,恰好都读7册书的概率为.22. 如图,数轴上的点A、B、C、D、E表示连续的五个整数,对应的数分别为a、b、c、d、e. (1)、若a+e=0,直接写出代数式b+c+d的值为:(2)、若a+b=7,先化简,再求值: :(3)、若a+b+c+d+e=5,数轴上的点M表示的实数为m,且MM+ME>12,则m的取值范围是 .23. 如图,在△ABC中,AB=CB=3,∠ABC=90°,点D为直线BC上一点,点E为AB延长线上一点,且BE=BD,连结AE、DE、EC.
(1)、若a+e=0,直接写出代数式b+c+d的值为:(2)、若a+b=7,先化简,再求值: :(3)、若a+b+c+d+e=5,数轴上的点M表示的实数为m,且MM+ME>12,则m的取值范围是 .23. 如图,在△ABC中,AB=CB=3,∠ABC=90°,点D为直线BC上一点,点E为AB延长线上一点,且BE=BD,连结AE、DE、EC.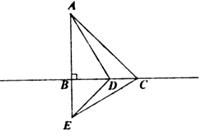 (1)、求证:△ABD≌△CBE:(2)、若∠CAD=15°,求∠BEC的度数.(3)、若点P是△CAD的外心,当点D在直线BC的一个位置运动到另一个位置时,点P恰好在△ABC的内部,请直接写出点P走过的距离为 .24. 如图,直线l1与y轴交于点A(0,3),直线l2:y=-x-2交y轴于点B,交直线l1点P(-3,t).
(1)、求证:△ABD≌△CBE:(2)、若∠CAD=15°,求∠BEC的度数.(3)、若点P是△CAD的外心,当点D在直线BC的一个位置运动到另一个位置时,点P恰好在△ABC的内部,请直接写出点P走过的距离为 .24. 如图,直线l1与y轴交于点A(0,3),直线l2:y=-x-2交y轴于点B,交直线l1点P(-3,t). (1)、求直线l1的函数解析式;(2)、过动点D(a,0)作x轴的垂线与直线l1、l2分别交于M、N两点,且MN≤3.
(1)、求直线l1的函数解析式;(2)、过动点D(a,0)作x轴的垂线与直线l1、l2分别交于M、N两点,且MN≤3.①求a的取值范围;
②若 S△ANB=2S△APN , 直接写出a的值.
25. 跳台滑雪是冬季奥运会比赛项目之一,如图平面直角坐标系是跳台滑雪的截面示意图,运动员沿滑道l下滑,在y轴上的点A起跳,点A距落地水平面x轴125m,运动员落地的雪面开始是段曲线m,到达点B后变为水平面,点B距y轴的水平距离为120m.运动员(看成点)从点A起跳后的水平速度为vm/s,点G是下落路线的某位置.忽略空气阻力,实验表明:G,A的竖直距离h(m)与飞出时间t(s)的平方成正比,且t=1时h=5;G,A的水平距离是vt米
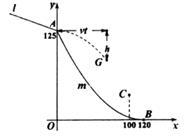 (1)、用含t的代数式表示h;(2)、用含v、t的代数式表示点G的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围);(3)、奥运组委会规定,运动员落地点距起跳点的水平距离为运动员本次跳跃的成绩,并且参赛的达标成绩为120m.在运动员跳跃的过程中,点C(100,35)处有一个摄像头,记录运动员的空中姿态,当运动员飞过点C时,在点C上方可被摄像头抓拍到.
(1)、用含t的代数式表示h;(2)、用含v、t的代数式表示点G的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围);(3)、奥运组委会规定,运动员落地点距起跳点的水平距离为运动员本次跳跃的成绩,并且参赛的达标成绩为120m.在运动员跳跃的过程中,点C(100,35)处有一个摄像头,记录运动员的空中姿态,当运动员飞过点C时,在点C上方可被摄像头抓拍到.若运动员本次跳跃达到达标成绩,并且能被C处摄像头抓拍,求从点A起跳后的水平速度v的取值范围.
26. 如图1,△OAB中,OA=OB=10,将扇形POP按图1摆放,使扇形的半径OP、OP分别与0A、OB重合,OP=6.如图2,若△AOB不动,让扇形POP绕点O逆时针旋转一周,连接线段AP、BP,设旋转角为a.
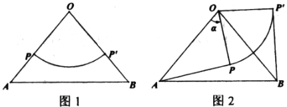
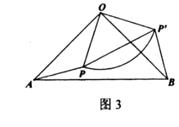
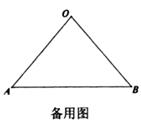
发现:直接写出AP、BP’的数量关系.
探究:若∠AOB=80°
(1)、扇形POP绕到点O的左侧,当OP∥AB时,旋转角a= °:(2)、扇形POP绕到点O的右侧,当AP与 相切时,求BP’;(3)、若点Q是弧 上任意一点,在扇形POP’绕点O逆时针转过程中,当△AOQ的面积最大时,直接写出∠BOQ的度数;延伸:如图3,若∠AOB==90°,当A、P、P'三点共线时,直接写出线段BP’的长.