河北省石家庄市十八中2018-2019学年中考数学二模考试试卷
试卷更新日期:2019-06-04 类型:中考模拟
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11-16小题各2分.)
-
1. 下列各数中,小于-3的数是( )A、1 B、0 C、-4 D、-22. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、(-a3)2=-a6 B、3x+2y=6xy C、3 -2 = D、 =34. 河北省“十三五”规划新建农林发电2.1×106千瓦.则2.1×106千瓦原数是( )A、0.0000021千瓦 B、210000千瓦 C、2100000千瓦 D、0.000021千瓦5. 下图是由多个相同小立方体搭成的几何体,则它的左视图为( )
3. 下列计算正确的是( )A、(-a3)2=-a6 B、3x+2y=6xy C、3 -2 = D、 =34. 河北省“十三五”规划新建农林发电2.1×106千瓦.则2.1×106千瓦原数是( )A、0.0000021千瓦 B、210000千瓦 C、2100000千瓦 D、0.000021千瓦5. 下图是由多个相同小立方体搭成的几何体,则它的左视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 已知反比例函数y= 的图象过二、四象限,则一次函数y=kx+k的图象大致是( )A、
6. 已知反比例函数y= 的图象过二、四象限,则一次函数y=kx+k的图象大致是( )A、 B、
B、 C、
C、 D、
D、 7. 已知方程组 的解为 ,则O、□分别为( )
7. 已知方程组 的解为 ,则O、□分别为( )
A、1,2 B、1,5 C、5,1 D、2,48. 证明:平行四边形对角线互相平分。已知:四边形ABCD是平行四边形,如图所示。求证:AO=CO,BO=DO.以下是排乱的证明过程,正确的顺序应是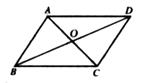
①∴∠ABO=∠CDO,∠BAC=∠DCA.②∵四边形ABCD是平行四边形.③∴AB∥CD,AB=DC.④△AOB≌△COD.⑤∴OA=OC,OB=OD
A、②-①-③-④-⑤ B、②-③-⑤-①-④ C、②-③-①-④-⑤ D、③-②-①-④-⑤9. 如图,在△ABC中,DE∥BC, ,则下列结论正确的是( ) A、 B、 C、 D、10. 在△ABC中,CA=CB=4,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰好在上(如图所示)。则图中阴影部分的面积为( )
A、 B、 C、 D、10. 在△ABC中,CA=CB=4,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰好在上(如图所示)。则图中阴影部分的面积为( )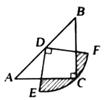 A、2π-4 B、4π-4 C、2π+4 D、4π+411. 在东西方向的海岸线上有A,B两个港口,甲货船从A港沿东北方向以5海里/时的速度出发,同时乙货船从B港口沿北偏西60°的方向出发,2h后相遇在点P处,如图所示.问A港与B港相距( )海里.
A、2π-4 B、4π-4 C、2π+4 D、4π+411. 在东西方向的海岸线上有A,B两个港口,甲货船从A港沿东北方向以5海里/时的速度出发,同时乙货船从B港口沿北偏西60°的方向出发,2h后相遇在点P处,如图所示.问A港与B港相距( )海里. A、10 B、5 +5 C、10+5 D、2012. 下表是某校合唱团成员的年龄分布,对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A、10 B、5 +5 C、10+5 D、2012. 下表是某校合唱团成员的年龄分布,对于不同的x,下列关于年龄的统计量不会发生改变的是( )年龄/岁
13
14
15
16
频数
5
15
x
10- x
A、平均数、中位数 B、众数、方差 C、平均数、方差 D、众数、中位数13. 某市对城区内某一段道路的一侧全部栽上梧桐树,要求路的两端各栽一棵,并且每两棵树的间隔相等,如果每隔4米栽1棵,则树苗缺21棵;如果每隔5米栽1棵,则树苗正好用完.设原有树苗x棵,根据题意列方程,正确的是( )A、4(x+21-1)=5(x-1) B、4(x+21)=5(x-1) C、4(x+21-1)=5x D、4(x+21)=5x14. 已知,在△ABC中,AB=AC,求作△ABC的外心O,以下是甲、乙两同学的作法:对于两人的作法:甲:如图
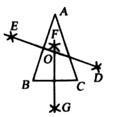
⑴作AB的垂直平分线DE;
⑵作BC的垂直平分线FG:
⑶DE,FG交于点O,则点O即为所求.
乙:如图
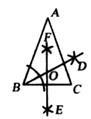 ,
,⑴作∠ABC的平分线BD;
⑵作BC的垂直平分线EF;图5图6
⑶BD,EF交于点O,则点O即为所求.
对于两人的作法,正确的是( )
A、两人都对 B、两人都不对 C、甲对,乙不对 D、甲不对,乙对15. 如图,在△ABC中,点I为△ABC的内心,点D在BC上,且ID⊥BC,若∠ABC=44°,∠C=56°,则∠AID的度数为( )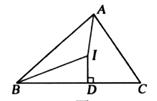 A、174° B、176° C、178° D、180°16. 如图,已知A(0,2),B(2,2),C(-1,0),抛物线y=a(x-h)2+k过点C,顶点M位于第一象限且在线段AB的垂直平分线上,若抛物线与线段AB无公共点,则k的取值范围是( )
A、174° B、176° C、178° D、180°16. 如图,已知A(0,2),B(2,2),C(-1,0),抛物线y=a(x-h)2+k过点C,顶点M位于第一象限且在线段AB的垂直平分线上,若抛物线与线段AB无公共点,则k的取值范围是( )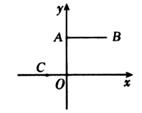 A、0<k<2 B、0<k<2或k> C、k> D、0<k<2或k>
A、0<k<2 B、0<k<2或k> C、k> D、0<k<2或k>二、填空题(本大题有3个小题,共12分,17-18小题各3分;19小题有2个空,每空3分)
-
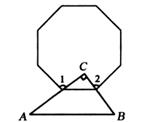
17. =18. 在图中,含30°的直角三角板的直角边AC,BC分别经过正八边形的两个顶点,则图中∠1+∠2= .
 19. 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,点P是线段AB上一动点.将△ABC绕点C按顺时针方向旋转,得到△A1B1C.点E是A1C上一点,且A1E=2,则PE长度的最小值为 , 最大值为.
19. 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,点P是线段AB上一动点.将△ABC绕点C按顺时针方向旋转,得到△A1B1C.点E是A1C上一点,且A1E=2,则PE长度的最小值为 , 最大值为.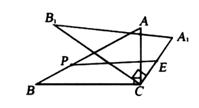
三、解答题(本大题有7个小题,共66分,解答应写出文字说明、证明过程或演算步骤)
-
20. 两个多项式A和B,A=
 ,B=x2+4x+4.A-B=3x2-4x-20.其中A被墨水污染了.
(1)、求多项式A.(2)、x取其中适合的一个数:2,-2,0,求 的值.21. 某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
,B=x2+4x+4.A-B=3x2-4x-20.其中A被墨水污染了.
(1)、求多项式A.(2)、x取其中适合的一个数:2,-2,0,求 的值.21. 某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题: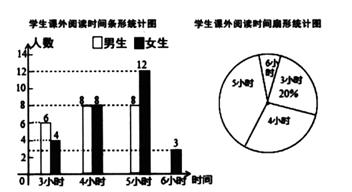 (1)、本次调查的学生总数为人,被调查学生的课外阅读时间的中位数是小时,众数是 小时;(2)、请你补全条形统计图 , 在扇形统计图中,课外阅读时间为5小时的扇形的圆心角度数是 :(3)、若全校九年级共有学生700人,估计九年级一周课外阅读时间为6小时的学生有多少人?(4)、若学校选取A、B、C、D四人参加阅读比赛,两人一组分为两组,求A与C是一组的概率。(列表或树状图)22. 已知P1=-2,P2=(-2)×(-2),P3=(-2)×(-2)×(-2),…,Pn=(-2)×(-2)x.…x(-2).(1)、计算P2+P3的值.(2)、猜想2P2018+P2019.(3)、猜想2PN+Pn+1·23. 如图,直线a∥b,点M,N分别为直线a和直线b上的点,连接M,N,∠1=70°,点P是线段MN上一动点,直线DE始终经过点P,且与直线a,b分别交与点D,E,设∠NPE=a.
(1)、本次调查的学生总数为人,被调查学生的课外阅读时间的中位数是小时,众数是 小时;(2)、请你补全条形统计图 , 在扇形统计图中,课外阅读时间为5小时的扇形的圆心角度数是 :(3)、若全校九年级共有学生700人,估计九年级一周课外阅读时间为6小时的学生有多少人?(4)、若学校选取A、B、C、D四人参加阅读比赛,两人一组分为两组,求A与C是一组的概率。(列表或树状图)22. 已知P1=-2,P2=(-2)×(-2),P3=(-2)×(-2)×(-2),…,Pn=(-2)×(-2)x.…x(-2).(1)、计算P2+P3的值.(2)、猜想2P2018+P2019.(3)、猜想2PN+Pn+1·23. 如图,直线a∥b,点M,N分别为直线a和直线b上的点,连接M,N,∠1=70°,点P是线段MN上一动点,直线DE始终经过点P,且与直线a,b分别交与点D,E,设∠NPE=a.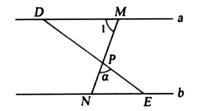 (1)、证明△MPD∽△NPE.(2)、当△MPD与△NPE全等时,直接写出点P的位置.(3)、当△NPE是等腰三角形时,求a的值.24. 如图,已知点A,B,C,D的坐标分别为(-2,2),(-2,1),(3,1),(3,2).线段AD,AB,BC组成的图形为图形G,点P沿D→A→B→C移动,设点P移动的距离为S,直线l:y=-x+b过点P,且在点P移动过程中,直线l随P运动而运动.
(1)、证明△MPD∽△NPE.(2)、当△MPD与△NPE全等时,直接写出点P的位置.(3)、当△NPE是等腰三角形时,求a的值.24. 如图,已知点A,B,C,D的坐标分别为(-2,2),(-2,1),(3,1),(3,2).线段AD,AB,BC组成的图形为图形G,点P沿D→A→B→C移动,设点P移动的距离为S,直线l:y=-x+b过点P,且在点P移动过程中,直线l随P运动而运动.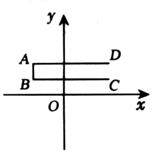 (1)、若点P过点D时,求直线l的解析式;(2)、当l过点C时,求S值;(3)、①若直线l与图形G有一个交点,直接写出b的取值范围;
(1)、若点P过点D时,求直线l的解析式;(2)、当l过点C时,求S值;(3)、①若直线l与图形G有一个交点,直接写出b的取值范围;②若直线l与图形G有两个交点,直接写出b的取值范围.
25. 在高尔夫球训练中,运动员在距球洞10m处击球,其飞行路线满足抛物线y=- x2+ x,其图象如图所示,其中球飞行高度为y(m),球飞行的水平距离为x(m),球落地时距球洞的水平距离为2m.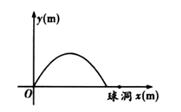 (1)、求b的值;(2)、若运动员再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球的飞行路线应满足怎样的抛物线,求抛物线的解析式;(3)、若球洞4m处有一横放的1.2m高的球网,球的飞行路线仍满足抛物线y=- x2+ x,要使球越过球网,又不越过球洞(刚好进洞),求b的取值范围.26. 如图,在△ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,半圆O的直径DE=12cm.点E与点C重合,半圆O以2cm/s的速度从左向右移动,在运动过程中,点D、E始终在BC所在的直线上.设运动时间为x(s),半圆O与△ABC的重叠部分的面积为S(cm2).
(1)、求b的值;(2)、若运动员再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球的飞行路线应满足怎样的抛物线,求抛物线的解析式;(3)、若球洞4m处有一横放的1.2m高的球网,球的飞行路线仍满足抛物线y=- x2+ x,要使球越过球网,又不越过球洞(刚好进洞),求b的取值范围.26. 如图,在△ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,半圆O的直径DE=12cm.点E与点C重合,半圆O以2cm/s的速度从左向右移动,在运动过程中,点D、E始终在BC所在的直线上.设运动时间为x(s),半圆O与△ABC的重叠部分的面积为S(cm2).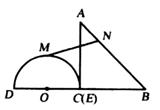 (1)、当x=0时,设点M是半圆O上一点,点N是线段AB上一点,则MN的最大值为 :MN的最小值为.(2)、在平移过程中,当点O与BC的中点重合时,求半圆O与△ABC重叠部分的面积S;(3)、当x为何值时,半圆O与△ABC的边所在的直线相切?
(1)、当x=0时,设点M是半圆O上一点,点N是线段AB上一点,则MN的最大值为 :MN的最小值为.(2)、在平移过程中,当点O与BC的中点重合时,求半圆O与△ABC重叠部分的面积S;(3)、当x为何值时,半圆O与△ABC的边所在的直线相切?