河北省衡水市八校2018-2019学年中考数学八模考试试卷
试卷更新日期:2019-06-04 类型:中考模拟
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.)
-
1. 下列图形中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列四个数表示在数轴上,它们对应的点中,离原点最远的是( )A、-2 B、-1 C、0 D、13. 下列运算正确的是( )A、x·x2 = x2 B、(xy)2 = xy2 C、(x2)3 = x6 D、x2 +x2 = x44. 学校开展捐书活动,以下是5名同学捐书的册数:4,9,5,x,3,已知这组数据的平均数是5,则这组数据的中位数和众数分别是( )A、3和3 B、4和4 C、3和4 D、5和55. 下图是由六个相同的小立方块搭成的几何体,这个几何体的俯视图是( )
2. 下列四个数表示在数轴上,它们对应的点中,离原点最远的是( )A、-2 B、-1 C、0 D、13. 下列运算正确的是( )A、x·x2 = x2 B、(xy)2 = xy2 C、(x2)3 = x6 D、x2 +x2 = x44. 学校开展捐书活动,以下是5名同学捐书的册数:4,9,5,x,3,已知这组数据的平均数是5,则这组数据的中位数和众数分别是( )A、3和3 B、4和4 C、3和4 D、5和55. 下图是由六个相同的小立方块搭成的几何体,这个几何体的俯视图是( )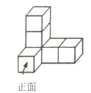 A、
A、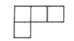 B、
B、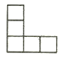 C、
C、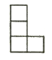 D、
D、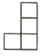 6. 2018年2月18日,清·袁枚的一首诗《苔》被乡村老师梁俊和山里的孩子小梁在《经典永流传》的舞台重新唤醒,“白日不到处,青春恰自来.苔花如米小,也学牡丹开。”若苔花的花粉直径约为0.0000084米,用科学记数法表示0.0000084=8.4×10n , 则n为( )A、-5 B、-6 C、5 D、67. 已知A(x1 , y1)和B(x2 , y2)是反比例函数y= 上的两个点,若x2>x1>0,则( )A、y2>y1>0 B、y1>y2>0 C、0>y1>y2 D、0>y2>y18.
6. 2018年2月18日,清·袁枚的一首诗《苔》被乡村老师梁俊和山里的孩子小梁在《经典永流传》的舞台重新唤醒,“白日不到处,青春恰自来.苔花如米小,也学牡丹开。”若苔花的花粉直径约为0.0000084米,用科学记数法表示0.0000084=8.4×10n , 则n为( )A、-5 B、-6 C、5 D、67. 已知A(x1 , y1)和B(x2 , y2)是反比例函数y= 上的两个点,若x2>x1>0,则( )A、y2>y1>0 B、y1>y2>0 C、0>y1>y2 D、0>y2>y18.如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为( )
 A、9 B、12 C、15 D、189. 用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A、9 B、12 C、15 D、189. 用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A、 B、
B、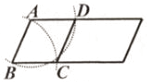 C、
C、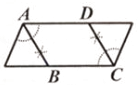 D、
D、 10. 如图,OA的方向是北偏东15°,OB的方向是西北方向,若∠AOC=∠A0B,则OC的( )
10. 如图,OA的方向是北偏东15°,OB的方向是西北方向,若∠AOC=∠A0B,则OC的( )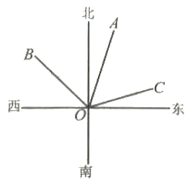 A、北偏东75° B、北偏东60° C、北偏东45° D、北偏东15°11. 在△ABC中,点D、E分别在AB、AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )A、= B、= C、= D、=12. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )
A、北偏东75° B、北偏东60° C、北偏东45° D、北偏东15°11. 在△ABC中,点D、E分别在AB、AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )A、= B、= C、= D、=12. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )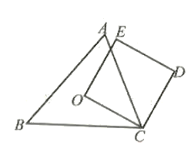 A、O是△AEB的外心,O是△AED的外心 B、O是△AEB的外心,O不是△AED的外心 C、O不是△AEB的外心,O是△AED的外心 D、O不是△AEB的外心,O不是△AED的外心13. 先化简,再求值: ,小明的解题步骤如下:
A、O是△AEB的外心,O是△AED的外心 B、O是△AEB的外心,O不是△AED的外心 C、O不是△AEB的外心,O是△AED的外心 D、O不是△AEB的外心,O不是△AED的外心13. 先化简,再求值: ,小明的解题步骤如下:原式= 第一步
= 第二步
= 第三步
= 第四步
请你判断一下小明的解题过程从第几步开始出错( )
A、第一步 B、第二步 C、第三步 D、第四步14. 有数颗等重的糖果和数个大、小砝码,其中大砝码皆为5克、小砝码皆为1克,如图是将糖果与砝码放在等臂天平上的两种情形。判断下列选项中哪一种情形是正确的( ) A、
A、 B、
B、 C、
C、 D、
D、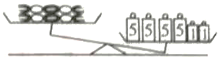 15. 如图,正方形ABCD的顶点B、C在x轴的正半轴上,反个比例函数y= (k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n, ),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )
15. 如图,正方形ABCD的顶点B、C在x轴的正半轴上,反个比例函数y= (k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n, ),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )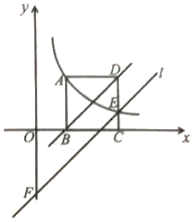 A、(0,- ) B、(0,- ) C、(0,-3) D、(0,- )16. 取一个自然数,若它是奇数,则乘以3加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1.这个结论在数学上还没有得到证明,但举例验证都是正确的.例如:取自然数5,经过下面5步运算可得1,即:如图所示.如果自然数m恰好经过7步运算可得到1,则所有符合条件的m的值有( )
A、(0,- ) B、(0,- ) C、(0,-3) D、(0,- )16. 取一个自然数,若它是奇数,则乘以3加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1.这个结论在数学上还没有得到证明,但举例验证都是正确的.例如:取自然数5,经过下面5步运算可得1,即:如图所示.如果自然数m恰好经过7步运算可得到1,则所有符合条件的m的值有( ) A、6个 B、5个 C、4个 D、3个
A、6个 B、5个 C、4个 D、3个二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有2个空,每空3分.)
-
17. 冬季某日,上海最低气温是3℃,北京最低气温是-5℃,这一天上海的最低气温比北京的最低气温高 ℃.
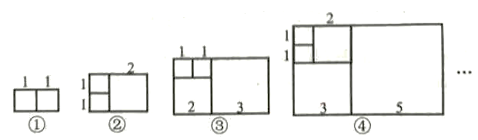
18. 若m2-n2=6,且m-n=3,则m+n= .19. 意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个,3个,4个,5个.正方形拼成如下长方形,若按此规律继续做长方形,则序号为⑦的长方形的长是 , 周长是 。
三、解答题(有7个小题,共66分)
-
20. 图中是小明完成的一道作业题,请你参考小明的解答方法解答下面的问题:
小明的作业
计算:(-4)7×0.257
解:(-4)7×0.257=(-4×0.25)7
=(-1)7
=-1
(1)、计算①82018×(-0.125)2018②(2)、看2·4n·16n=219 , 求n的值21. 某厂为新型号电视机上市举办促销活动,顾客每买一台该型号电视机,可获得一次抽奖机会,该厂拟按10%设大奖,其余90%为小奖。广家设计的抽奖方案是:在一个不透明的盒子中,放入10个黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球的顾客获得大奖,摸到白球的顾客获得小奖。(1)、厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2个黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖。该抽奖方案符合厂家的设奖要求吗?请说明理由;(2)、下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上黄、白两种颜色,并设计抽奖方案,使其符合厂家的设奖要求。(友情提醒:1.转盘上用文字注明颜色和扇形的圆心角的度数;2.结合转盘简述获奖方式,不需说明理由.)22. 自习课上小明在准备完成题目:化简:( x2+6x+8)-(6x+8x2+2)发现系数“
x2+6x+8)-(6x+8x2+2)发现系数“  ”
” 印刷不清楚、
(1)、他把“ ”猜成6,请你帮小明完成化简:(6x2+6x+8)-(6x+8x2+2); (2)、小明同桌看到他化简的结果说:“你猜错了,我看到该题标准答案的结果是常数。”请你通过计算说明原题中“
”猜成6,请你帮小明完成化简:(6x2+6x+8)-(6x+8x2+2); (2)、小明同桌看到他化简的结果说:“你猜错了,我看到该题标准答案的结果是常数。”请你通过计算说明原题中“ ”是几? 23. 如图,∠A=∠B=30°,P为AB中点,线段MV绕点P旋转,且M为射线AC上(不与点d重合)的任意一点,且N为射线BD上(不与点B重合)的一点,设∠BPN=α.
”是几? 23. 如图,∠A=∠B=30°,P为AB中点,线段MV绕点P旋转,且M为射线AC上(不与点d重合)的任意一点,且N为射线BD上(不与点B重合)的一点,设∠BPN=α.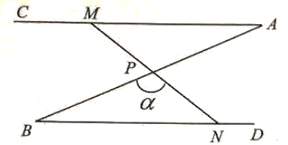 (1)、求证:△APM≌△BPN;(2)、当MN=2BN时,求α的度数;(3)、若AB=4,60°≤α≤90°,直接写出△BPN的外心运动路线的长度。24. 山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车1月份销售总额为50000元,2月份销售总额将比1月份减少20%,每辆销售价比1月份降低400元,若这两个月卖出的数量相同。(1)、求2月份A型车每辆售价多少元?(2)、该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,求销售这批车获得的最大利润是多少元?
(1)、求证:△APM≌△BPN;(2)、当MN=2BN时,求α的度数;(3)、若AB=4,60°≤α≤90°,直接写出△BPN的外心运动路线的长度。24. 山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车1月份销售总额为50000元,2月份销售总额将比1月份减少20%,每辆销售价比1月份降低400元,若这两个月卖出的数量相同。(1)、求2月份A型车每辆售价多少元?(2)、该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,求销售这批车获得的最大利润是多少元?A、B两种型号车今年的进货和销售价格表:
A型车
B型车
进货价格(元)
1100
1400
销售价格(元)
2月份的销售价格
2000
25. 如图,形如量角器的半圆O的直径DE-12cm,形如三角板的△ABC中,∠ACB=90°,tan∠ABC= ,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm. (1)、点C到直线AB的距离为 cm;(2)、当t= (s)时,⊙O与AC所在直线第一次相切;当t=(s)时,⊙O与AC所在直线第二次相切;(3)、当t为何值时,直线AB与半圆O所在的圆相切;(4)、当△ABC的一边所在直线与圆O相切时,若⊙O与△ABC有重叠部分,直接写出重叠部分的面积。26. 已知,抛物线C1:y=- x2+mx+m+
(1)、点C到直线AB的距离为 cm;(2)、当t= (s)时,⊙O与AC所在直线第一次相切;当t=(s)时,⊙O与AC所在直线第二次相切;(3)、当t为何值时,直线AB与半圆O所在的圆相切;(4)、当△ABC的一边所在直线与圆O相切时,若⊙O与△ABC有重叠部分,直接写出重叠部分的面积。26. 已知,抛物线C1:y=- x2+mx+m+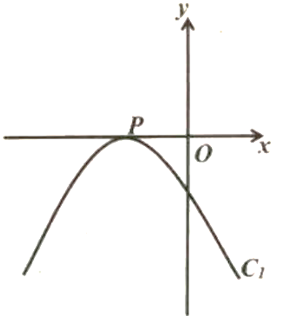 (1)、①当m=1时,抛物线与x轴的交点坐标为
(1)、①当m=1时,抛物线与x轴的交点坐标为②当m=2时,抛物线与x轴的交点坐标为:
(2)、①无论m取何值,抛物线经过定点P:②随着m的取值的变化,顶点M(x,y)随之变化,y是x的函数,记为函数C2 , 则函数C2的关系式为: ;
(3)、如图,若抛物线C1与x轴仅有一个公共点时,①直接写出此时抛物线C1的函数关系式;
②请在图中画出顶点M满足的函数C2的大致图象,在x轴上任取一点C,过点C作平行于y轴的直线l分别交C1、C2于点A、B,若△PAB为等腰直角三角形,求点C的坐标;
(4)、二次函数的图象C2与y轴交于点N,连接PN,若二次函数的图象C1与线段PN有两个交点,直接写出m的取值范围.