河北省2018-2019学年中考数学五模考试试卷
试卷更新日期:2019-06-04 类型:中考模拟
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分)
-
1. 下列图形中是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 实数a,b,c,d在数轴上的对应点的位置如图所示,则这四个数中,相反数是正数的( )
2. 实数a,b,c,d在数轴上的对应点的位置如图所示,则这四个数中,相反数是正数的( ) A、a B、b C、c D、d3. 下图是由7个完全相同的小立方块搭成的几何体,那么这个几何体的左视图是( )
A、a B、b C、c D、d3. 下图是由7个完全相同的小立方块搭成的几何体,那么这个几何体的左视图是( )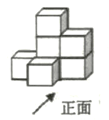 A、
A、 B、
B、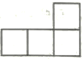 C、
C、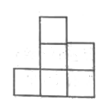 D、
D、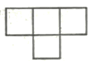 4. 北京城市副中心生态文明建设在2016年取得突出成果,通过大力推进能源结构调整,热电替代供热面积为17960000平方米.将17960000用科学记数法表示应为( )A、1.796×106 B、17.96×106 C、1.796×107 D、0.1796×1075. 下列运算中,正确的是( )A、a2·a3=a6 B、(-a2)3=a6 C、-3a-2=- D、-a2-2a2=-3a26. 估计7-2 的值在( )A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间。7. 有15位学生参加学校组织的“爱我中华”演讲比赛,比赛结后根据每位学生的最后得分计算出平均数、中位数、众数、方差。如果修改规则:先去掉一个最高分,去掉一个最低分,再进行统计,则上述四个统计量中,一定不会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差8. 如图,将一张矩形的纸从下向上对折,顺时针旋转90°后再对折,然后沿着下图中的虚线剪下,则剪下的纸片打开后的形状一定为( )
4. 北京城市副中心生态文明建设在2016年取得突出成果,通过大力推进能源结构调整,热电替代供热面积为17960000平方米.将17960000用科学记数法表示应为( )A、1.796×106 B、17.96×106 C、1.796×107 D、0.1796×1075. 下列运算中,正确的是( )A、a2·a3=a6 B、(-a2)3=a6 C、-3a-2=- D、-a2-2a2=-3a26. 估计7-2 的值在( )A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间。7. 有15位学生参加学校组织的“爱我中华”演讲比赛,比赛结后根据每位学生的最后得分计算出平均数、中位数、众数、方差。如果修改规则:先去掉一个最高分,去掉一个最低分,再进行统计,则上述四个统计量中,一定不会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差8. 如图,将一张矩形的纸从下向上对折,顺时针旋转90°后再对折,然后沿着下图中的虚线剪下,则剪下的纸片打开后的形状一定为( )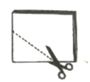 A、三角形 B、菱形 C、矩形 D、正方形9. 化简 的结果是( )A、x+1 B、 C、x-1 D、10. 在平面直角坐标系中,O为原点,小明将一块等腰直角三角板ABO放在这个平面直角坐标系中,如图.若点A的坐标为(6,8),则点B的坐标为( )
A、三角形 B、菱形 C、矩形 D、正方形9. 化简 的结果是( )A、x+1 B、 C、x-1 D、10. 在平面直角坐标系中,O为原点,小明将一块等腰直角三角板ABO放在这个平面直角坐标系中,如图.若点A的坐标为(6,8),则点B的坐标为( )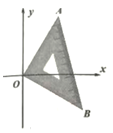 A、(-6,8) B、(6,-8) C、(-8,6) D、(8,-6)11. 如图,已知平行四边形AOBC的顶点O(0,0),A(-1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
A、(-6,8) B、(6,-8) C、(-8,6) D、(8,-6)11. 如图,已知平行四边形AOBC的顶点O(0,0),A(-1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )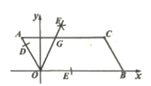 A、( -1,2) B、( ,2) C、(3- ,2) D、( -2,2)12. 如图,在△ABC中,AB是⊙O的直径,∠B=60°,∠C=70°,则∠BOD的度数是( )
A、( -1,2) B、( ,2) C、(3- ,2) D、( -2,2)12. 如图,在△ABC中,AB是⊙O的直径,∠B=60°,∠C=70°,则∠BOD的度数是( )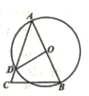 A、90° B、100° C、110° D、120°13. 某工厂进行技术创新,现在每天比原来多生产50台机器,并且现在生产600台机器所需时间与原计划生产450台机器所需时间相同。设现在每天生产x台机器,可得( )A、 B、 C、 D、14. 如图,△ABC中,下面说法正确的个数是( )
A、90° B、100° C、110° D、120°13. 某工厂进行技术创新,现在每天比原来多生产50台机器,并且现在生产600台机器所需时间与原计划生产450台机器所需时间相同。设现在每天生产x台机器,可得( )A、 B、 C、 D、14. 如图,△ABC中,下面说法正确的个数是( )
①若O是△ABC的外心,∠A=50°,则∠BOC=100°;②若O是△ABC的内心,∠A=50°,则∠BOC=115°;③若BC=6,AB+AC=10,则△ABC的面积的最大值是12;④△ABC的面积是12,周长是16,则其内切圆的半径是1.
A、1个 B、2个 C、3个 D、4个15. 已知二次函数y=ax2+bx+c中,自变量x与函数y之间的部分对应值如表:x
…..
0
1
2
3
…..
y
…..
-1
2
3
2
….
在该函数的图象上有A(x1 , y1)和B(x2 , y2)两点,且-1<x1≤0,3<x2<4,y1与y2的大小关系正确的是
A、y1≥y2 B、y1>y2 C、y1≤y2 D、y1≤y216. 如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与O刻度线的一端重合,∠ABC=40°,射线CD绕点C转动,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是( )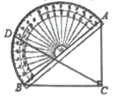 A、40° B、70° C、80或140° D、80°或70°
A、40° B、70° C、80或140° D、80°或70°二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有2个空,每空3分.)
-
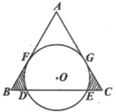
17. 已知点A(a,1)与点B(5,b)关于原点对称,则ab的值为.18. 如图,已知等边△ABC的边长是10 ,⊙O切AB、AC于点F、G,交边BC于D、E,⊙O的半径是6,则图中阴影部分的面积等于。
 19. 如图,在函数y=(x>0)的图象上有点P1、P2、P3..……Pn、Pn+1 点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、Pn、Pn+1分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3..…Sn , 则S1= , Sn=.(用含n的代数式表示)
19. 如图,在函数y=(x>0)的图象上有点P1、P2、P3..……Pn、Pn+1 点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、Pn、Pn+1分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3..…Sn , 则S1= , Sn=.(用含n的代数式表示)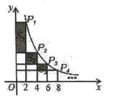
三、解答题(本大题有7个小题,共66分.)
-
20. 阅读材料:对于任何实数,我们规定符号 的意义是 =ad-bc.
例如: =1x4-2×3= =(-2)×5-4×3=-22
(1)、按照这个规定请你计算 的值;(2)、按照这个规定请你计算:当x2-4x+4=0时, 的值21. 某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动。某中学就“学生体育活动兴趣爱好“的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图: (1)、在这次调查中,喜欢篮球项目的同学有人,在扇形统计图中,乒乓球的百分比为%,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目。(2)、请将条形统计图补充完整,(3)、在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学。现要从中随机抽取2名同学代表班级参加篮球队,请求出所抽取的2名同学恰好是1名女同学和1名男同学的概率。22. “分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法。例如:图1有6个点,图2有12个点,图3有18个点,.…,按此规律,求图10、图n有多少个点?(1)、解决问题:我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图a,b,c),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是个、个.
(1)、在这次调查中,喜欢篮球项目的同学有人,在扇形统计图中,乒乓球的百分比为%,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目。(2)、请将条形统计图补充完整,(3)、在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学。现要从中随机抽取2名同学代表班级参加篮球队,请求出所抽取的2名同学恰好是1名女同学和1名男同学的概率。22. “分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法。例如:图1有6个点,图2有12个点,图3有18个点,.…,按此规律,求图10、图n有多少个点?(1)、解决问题:我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图a,b,c),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是个、个.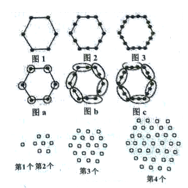 (2)、问题拓展:请你参考以上“分块计数法”,先将下面的点阵进行分块,再完成以下问题;
(2)、问题拓展:请你参考以上“分块计数法”,先将下面的点阵进行分块,再完成以下问题;第5个点阵中有个圆圈;第n个点阵中有个圆圈.
(3)、小圆圈的个数会等于271吗?如果会,请求出是第几个点阵:如果不会,请说明理由.23. 小明驾车从甲地到乙地,设他出发第xmin时的速度为ykm/h,图中的折线表示他在整个驾车过程中y与x之间的函数关系.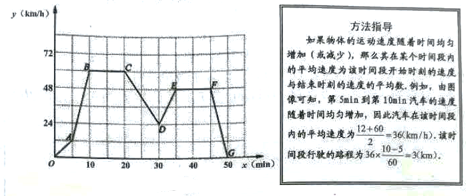 (1)、当20≤x≤30时,汽车的平均速度为km/h,该段时间行驶的路程为km;(2)、当30≤x≤35时,求y与x之间的函数关系式,并求出小明出发第32min时的速度;(3)、如果汽车每行驶100km耗油8L,那么小明驾车从甲地到乙地共耗油多少升?24. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)、当20≤x≤30时,汽车的平均速度为km/h,该段时间行驶的路程为km;(2)、当30≤x≤35时,求y与x之间的函数关系式,并求出小明出发第32min时的速度;(3)、如果汽车每行驶100km耗油8L,那么小明驾车从甲地到乙地共耗油多少升?24. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.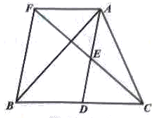 (1)、求证:BD=CD.(2)、如果AB=AC,试判断四边形AFBD的形状,并证明你的结论。25. 如图①,AB是半圆O的直径,以OA为直径作半圆C,P是半圆C上的一个动点(P与点A,O不重合),AP的延长线交半圆O于点D,其中OA=4,
(1)、求证:BD=CD.(2)、如果AB=AC,试判断四边形AFBD的形状,并证明你的结论。25. 如图①,AB是半圆O的直径,以OA为直径作半圆C,P是半圆C上的一个动点(P与点A,O不重合),AP的延长线交半圆O于点D,其中OA=4,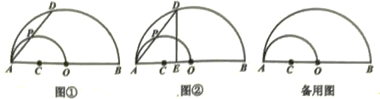 (1)、判断线段AP与PD的大小关系,并说明理由:(2)、连接OD,当OD与半圆C相切时,求弧AP的长:(3)、过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.26. 在平面直角坐标系xOy中,过y轴上一点A作平行于x轴的直线交某函数图象于点D,点P是x轴上一动点,连接DP,过点P作DP的垂线交y轴于点E(E在线段OA上,E不与点O重合),则称∠DPE为点D,P,E的“平横纵直角”图1为点D,P,E的“平横纵直角”的示意图.
(1)、判断线段AP与PD的大小关系,并说明理由:(2)、连接OD,当OD与半圆C相切时,求弧AP的长:(3)、过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.26. 在平面直角坐标系xOy中,过y轴上一点A作平行于x轴的直线交某函数图象于点D,点P是x轴上一动点,连接DP,过点P作DP的垂线交y轴于点E(E在线段OA上,E不与点O重合),则称∠DPE为点D,P,E的“平横纵直角”图1为点D,P,E的“平横纵直角”的示意图.如图2,在平面直角坐标系xOy中,已知二次函数图象与y轴交于点F(0,m),与x轴分别交于点B(-3,0),C(12,0).若过点F作平行于x轴的直线交抛物线于点N.
 (1)、点N的横坐标为;(2)、已知一直角为点N,M,K的“平横纵直角”,若在线段OC上存在不同的两点M1、M2 , 使相应的点K1、K2都与点F重合,试求m的取值范围;(3)、设抛物线的顶点为点Q,连接BQ与FN交于点H,当45°≤∠QHN≤60°时,求m的取值范围。
(1)、点N的横坐标为;(2)、已知一直角为点N,M,K的“平横纵直角”,若在线段OC上存在不同的两点M1、M2 , 使相应的点K1、K2都与点F重合,试求m的取值范围;(3)、设抛物线的顶点为点Q,连接BQ与FN交于点H,当45°≤∠QHN≤60°时,求m的取值范围。