上海市徐汇区2018-2019学年中考数学一模考试试卷
试卷更新日期:2019-06-04 类型:中考模拟
一、单选题
-
1. 某零件长40厘米,若该零件在设计图上的长是2毫米,则这幅设计图的比例尺是( )A、1:2000 B、1:200 C、200:1 D、2000:12. 将抛物线y=x2向右平移1个单位长度,再向上平移2个单位长度所得的抛物线解析式为( )A、y=(x﹣1)2+2 B、y=(x+1)2+2 C、y=(x﹣1)2﹣2 D、y=(x+1)2﹣23. 若斜坡的坡比为1: ,则斜坡的坡角等于( )A、30° B、45° C、50° D、60°4. 如图,下列条件中不能判定△ACD∽△ABC的是( )
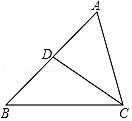 A、∠ADC=∠ACB B、 C、∠ACD=∠B D、AC2=AD•AB5. 若 =2 ,向量 和向量 方向相反,且| |=2| |,则下列结论中错误的是( )A、| |=2 B、| |=4 C、 =4 D、 =6. 已知抛物线y=ax2+bx+c上部分点的横坐标x与纵坐标y的对应值如下表:
A、∠ADC=∠ACB B、 C、∠ACD=∠B D、AC2=AD•AB5. 若 =2 ,向量 和向量 方向相反,且| |=2| |,则下列结论中错误的是( )A、| |=2 B、| |=4 C、 =4 D、 =6. 已知抛物线y=ax2+bx+c上部分点的横坐标x与纵坐标y的对应值如下表:x
…
﹣1
0
1
2
3
…
y
…
3
0
﹣1
m
3
…
①抛物线开口向下②抛物线的对称轴为直线x=﹣1③m的值为0④图象不经过第三象限
上述结论中正确的是( )
A、①④ B、②④ C、③④ D、②③二、填空题
-
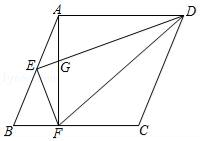
7. 已知 ,则 的值是 .8. 已知点P是线段AB上的黄金分割点,AP>BP,AB=4,那么AP= .9. 计算: ( ﹣2 )﹣4 = .10. 已知A(﹣2,y1)、B(﹣3,y2)是抛物线y=(x﹣1)2+c上两点,则y1y2 . (填“>”、“=”或“<”)11. 如图,在▱ABCD中,AB=3,AD=5,AF分别交BC于点E、交DC的延长线于点F , 且CF=1,则CE的长为 .
 12. 在Rt△ABC中,∠C=90°,AB=5,BC=3,则sinA= .13. 如图,正方形DEFG的边EF在ABC的边BC上,顶点D、G分别在边AB、AC上.已知BC长为40厘米,若正方形DEFG的边长为25厘米,则ABC的高AH为厘米.
12. 在Rt△ABC中,∠C=90°,AB=5,BC=3,则sinA= .13. 如图,正方形DEFG的边EF在ABC的边BC上,顶点D、G分别在边AB、AC上.已知BC长为40厘米,若正方形DEFG的边长为25厘米,则ABC的高AH为厘米.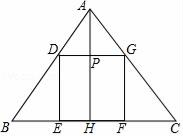 14. 如图,在梯形ABCD中,AD∥BC , EF是梯形ABCD的中位线,AH∥CD分别交EF、BC于点G、H , 若 = , = ,则用 、 表示 = .
14. 如图,在梯形ABCD中,AD∥BC , EF是梯形ABCD的中位线,AH∥CD分别交EF、BC于点G、H , 若 = , = ,则用 、 表示 = .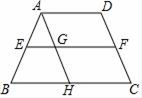 15. 如图,在Rt△ABC中,∠ACB=90°,点G是△ABC的重心,CG=2,sin∠ACG= ,则BC长为 .
15. 如图,在Rt△ABC中,∠ACB=90°,点G是△ABC的重心,CG=2,sin∠ACG= ,则BC长为 .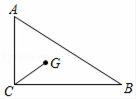 16. 如图,某兴趣小组用无人机进行航拍测高,无人机从1号楼和2号楼的地面正中间B点垂直起飞到高度为50米的A处,测得1号楼顶部E的俯角为60°,测得2号楼顶部F的俯角为45°.已知1号楼的高度为20米,则2号楼的高度为米(结果保留根号).
16. 如图,某兴趣小组用无人机进行航拍测高,无人机从1号楼和2号楼的地面正中间B点垂直起飞到高度为50米的A处,测得1号楼顶部E的俯角为60°,测得2号楼顶部F的俯角为45°.已知1号楼的高度为20米,则2号楼的高度为米(结果保留根号). 17. 如图,在△ABC中,AB=AC , BD=CD , CE⊥AB于点E , cosB= ,则 = .
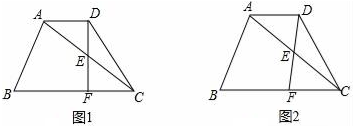
17. 如图,在△ABC中,AB=AC , BD=CD , CE⊥AB于点E , cosB= ,则 = . 18. 在梯形ABCD中,AB∥DC , ∠B=90°,BC=6,CD=2,tanA= .点E为BC上一点,过点E作EF∥AD交边AB于点F . 将△BEF沿直线EF翻折得到△GEF , 当EG过点D时,BE的长为 .
18. 在梯形ABCD中,AB∥DC , ∠B=90°,BC=6,CD=2,tanA= .点E为BC上一点,过点E作EF∥AD交边AB于点F . 将△BEF沿直线EF翻折得到△GEF , 当EG过点D时,BE的长为 .
三、解答题
-
19. 计算: .20. 如图,已知△ABC , 点D在边AC上,且AD=2CD , AB∥EC , 设 = , = .
 (1)、试用 、 表示 ;(2)、在图中作出 在 、 上的分向量,并直接用 、 表示 .21. 如图,在平面直角坐标系xOy中,抛物线y=﹣ x2+bx+c与x轴交于点A(﹣3,0)和点B , 与y轴交于点C (0,2).
(1)、试用 、 表示 ;(2)、在图中作出 在 、 上的分向量,并直接用 、 表示 .21. 如图,在平面直角坐标系xOy中,抛物线y=﹣ x2+bx+c与x轴交于点A(﹣3,0)和点B , 与y轴交于点C (0,2). (1)、求抛物线的表达式,并用配方法求出顶点D的坐标;(2)、若点E是点C关于抛物线对称轴的对称点,求tan∠CEB的值.22. 如图是某品牌自行车的最新车型实物图和简化图,它在轻量化设计、刹车、车篮和座位上都做了升级.A为后胎中心,经测量车轮半径AD为30cm , 中轴轴心C到地面的距离CF为30cm , 座位高度最低刻度为155cm , 此时车架中立管BC长为54cm , 且∠BCA=71°.(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.88)
(1)、求抛物线的表达式,并用配方法求出顶点D的坐标;(2)、若点E是点C关于抛物线对称轴的对称点,求tan∠CEB的值.22. 如图是某品牌自行车的最新车型实物图和简化图,它在轻量化设计、刹车、车篮和座位上都做了升级.A为后胎中心,经测量车轮半径AD为30cm , 中轴轴心C到地面的距离CF为30cm , 座位高度最低刻度为155cm , 此时车架中立管BC长为54cm , 且∠BCA=71°.(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.88) (1)、求车座B到地面的高度(结果精确到1cm);(2)、根据经验,当车座B'到地面的距离B'E'为90cm时,身高175cm的人骑车比较舒适,此时车架中立管BC拉长的长度BB'应是多少?(结果精确到1cm)
(1)、求车座B到地面的高度(结果精确到1cm);(2)、根据经验,当车座B'到地面的距离B'E'为90cm时,身高175cm的人骑车比较舒适,此时车架中立管BC拉长的长度BB'应是多少?(结果精确到1cm)