辽宁省本溪市2018-2019学年中考数学一模考试试卷
试卷更新日期:2019-06-04 类型:中考模拟
一、单选题
-
1. 在﹣7,5,0,﹣3这四个数中,最大的数是( )A、﹣7 B、5 C、0 D、﹣32. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
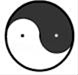 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、(xy)3=xy3 B、x5÷x5=x C、3x2·5x3=15x5 D、5x2y3+2x2y3=10x4y94. 如图所示的某零件左视图是( )
3. 下列计算正确的是( )A、(xy)3=xy3 B、x5÷x5=x C、3x2·5x3=15x5 D、5x2y3+2x2y3=10x4y94. 如图所示的某零件左视图是( )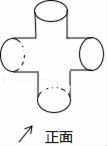 A、
A、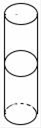 B、
B、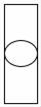 C、
C、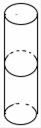 D、
D、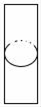 5. 某车间需加工一批零件,车间20名工人每天加工零件数如表所示:
5. 某车间需加工一批零件,车间20名工人每天加工零件数如表所示:每天加工零件数
4
5
6
7
8
人数
3
6
5
4
2
每天加工零件数的中位数和众数为( )
A、6,5 B、6,6 C、5,5 D、5,66. 下列事件为必然事件的是( )A、掷一枚普通的正方体骰子,掷得的点数不小于1 B、任意购买一张电影票,座位号是奇数 C、抛一枚普通的硬币,正面朝上 D、一年有367天7. 若一次函数y=(2m﹣3)x﹣1+m的图象不经过第三象限,则m的取值范围是( )A、1<m< B、1≤m< C、1<m≤ D、1≤m≤8. 体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,由题意列出关于x与y的方程组为( )进球数
0
1
2
3
4
5
人数
1
5
x
y
3
2
A、 B、 C、 D、9. 如图,过反比例函数y= (x<0)图象上的一点A作AB⊥x轴于点B , 连接AO , 若S△AOB=2,则k的值是( ) A、2 B、﹣2 C、4 D、﹣410. 如图1,在菱形ABCD中,∠BAD=120°,点Q是BC边的中点,点P为AB边上的一个动点,设AP=x , 图1中线段PQ的长为y , 若表示y与x的函数关系的图象如图2所示,则菱形ABCD的面积为( )
A、2 B、﹣2 C、4 D、﹣410. 如图1,在菱形ABCD中,∠BAD=120°,点Q是BC边的中点,点P为AB边上的一个动点,设AP=x , 图1中线段PQ的长为y , 若表示y与x的函数关系的图象如图2所示,则菱形ABCD的面积为( )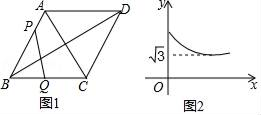 A、4 B、2 C、8 D、12
A、4 B、2 C、8 D、12二、填空题
-
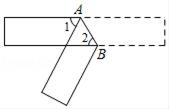
11. 将473000用科学记数法表示为 .12. 分解因式:3x2﹣6x2y+3xy2= .13. 如图,把一张长方形纸片沿AB折叠后,若∠1=48°,则∠2的大小为度.
 14. 在一个不透明的布袋中装有4个白球和n个黄球,它们除颜色不同外,其余均相同,若从中随机摸出一个球,摸到白球的概率是 ,则n= .15. 不等式组 的解集为 .16. 已知:如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,8),点D是OA的中点,点P在边BC上运动,当△ODP是腰长为10的等腰三角形时,则P点的坐标为 .
14. 在一个不透明的布袋中装有4个白球和n个黄球,它们除颜色不同外,其余均相同,若从中随机摸出一个球,摸到白球的概率是 ,则n= .15. 不等式组 的解集为 .16. 已知:如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,8),点D是OA的中点,点P在边BC上运动,当△ODP是腰长为10的等腰三角形时,则P点的坐标为 .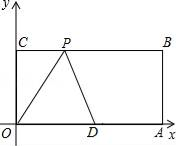 17. 如图,平面直角坐标系中,已知P(1,1),C为y轴正半轴上一点,D为第一象限内一点,且PC=PD , ∠CPD=90°,过点D作直线AB⊥x轴于B , 直线AB与直线y=x交于点A , 且BD=3AD , 连接CD , 直线CD与直线y=x交于点Q , 则点Q的坐标为 .
17. 如图,平面直角坐标系中,已知P(1,1),C为y轴正半轴上一点,D为第一象限内一点,且PC=PD , ∠CPD=90°,过点D作直线AB⊥x轴于B , 直线AB与直线y=x交于点A , 且BD=3AD , 连接CD , 直线CD与直线y=x交于点Q , 则点Q的坐标为 .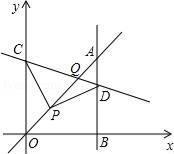
三、解答题
-
18. 已知 是关于 的方程 的一个根,则 __19. 先化简,再求值: ,其中 .20. 济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.
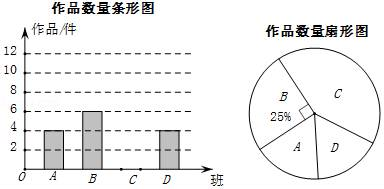
请根据以上信息,回答下列问题:
(1)、杨老师采用的调查方式是(填“普查”或“抽样调查”);(2)、请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .(3)、请估计全校共征集作品的件数.(4)、如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.21. 如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.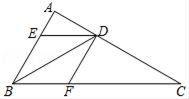 (1)、求证:四边形BEDF为菱形;(2)、如果∠A=90°,∠C=30°,BD=6,求菱形BEDF的面积.22. 如图:007渔船在南海海面上沿正东方向匀速航行,在A点观测到渔船C在北偏东60°方向的我国某传统渔场捕鱼作业.若007渔船航向不变,航行半小时后到达B点,观测到渔船C在东北方向上.问:007渔船再按原航向航行多长时间,离渔船C的距离最近?
(1)、求证:四边形BEDF为菱形;(2)、如果∠A=90°,∠C=30°,BD=6,求菱形BEDF的面积.22. 如图:007渔船在南海海面上沿正东方向匀速航行,在A点观测到渔船C在北偏东60°方向的我国某传统渔场捕鱼作业.若007渔船航向不变,航行半小时后到达B点,观测到渔船C在东北方向上.问:007渔船再按原航向航行多长时间,离渔船C的距离最近?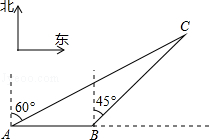 23. 某商店以15元/件的价格购进一批纪念品销售,经过市场调查发现:若每件卖20元,则每天可以售出50件,且售价每提高1元,每天的销量会减少2件,于是该商店决定提价销售,设售价x元件,每天获利y元.(1)、求每件售价为多少元时,每天获得的利润最大?最大利润是多少?(2)、若该商店雇用人员销售,在营销之前,对支付给销售人员的工资有如下两种方案:
23. 某商店以15元/件的价格购进一批纪念品销售,经过市场调查发现:若每件卖20元,则每天可以售出50件,且售价每提高1元,每天的销量会减少2件,于是该商店决定提价销售,设售价x元件,每天获利y元.(1)、求每件售价为多少元时,每天获得的利润最大?最大利润是多少?(2)、若该商店雇用人员销售,在营销之前,对支付给销售人员的工资有如下两种方案:方案一:每天支付销售工资100元,无提成;
方案二:每销售一件提成2元,不再支付销售工资.
综合以上所有信息,请你帮着该商店老板算一算,应该采用哪种支付方案,才能使该商店每天销售该纪念品的利润最大?最大利润是多少?
24. 已知△ABC内接于以AB为直径的⊙O , 过点C作⊙O的切线交BA的延长线于点D , 且DA∶AB=1∶2.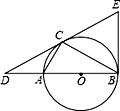 (1)、求∠CDB的度数;(2)、在切线DC上截取CE=CD , 连接EB , 判断直线EB与⊙O的位置关系,并证明.25. 如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)、求∠CDB的度数;(2)、在切线DC上截取CE=CD , 连接EB , 判断直线EB与⊙O的位置关系,并证明.25. 如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.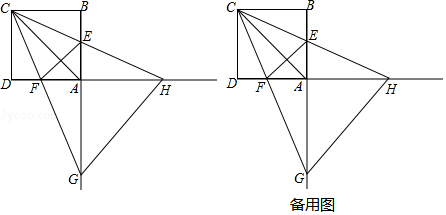 (1)、填空:∠AHC∠ACG;(填“>”或“<”或“=”)(2)、线段AC,AG,AH什么关系?请说明理由;(3)、设AE=m,
(1)、填空:∠AHC∠ACG;(填“>”或“<”或“=”)(2)、线段AC,AG,AH什么关系?请说明理由;(3)、设AE=m,①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
26. 如图1,抛物线y=mx2﹣4mx+3m(m>0)与x轴交于A , B两点(点B在点A右侧).与y轴交点C , 与直线l:y=x+1交于D、E两点,
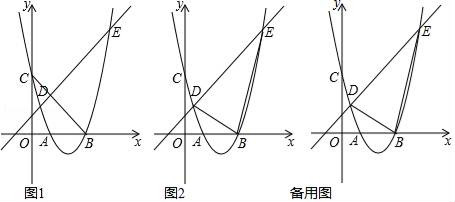 (1)、当m=1时,连接BC , 求∠OBC的度数;(2)、在(1)的条件下,连接D
(1)、当m=1时,连接BC , 求∠OBC的度数;(2)、在(1)的条件下,连接DB、EB , 是否存在抛物线在第四象限上一点P , 使得S△DBE=S△DPE?若存在,求出此时P点坐标及PB的长度;若不存在,请说明理由;
(3)、若以DE为直径的圆恰好与x轴相切,求此时m的值.