广东省惠来县2018-2019学年中考数学模拟考试试卷

试卷更新日期：2019-06-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、（x﹣y）²=x²﹣y² B、x²•x⁴=x⁶ C、^{$\sqrt{{(- 3)}^{2}} = - 3$} D、（2x²）³=6x⁶

查看试题解析
2. 据悉，超级磁力风力发电机可以大幅度提升风力发电效率，但其造价高昂，每座磁力风力发电机，其建造花费估计要5 300万美元，“5 300万”用科学记数法可表示为（）

A、5.3×10³ B、5.3×10⁴ C、5.3×10⁷ D、5.3×10⁸

查看试题解析
3. 如图，空心圆柱的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 正多边形的一个内角是150°，则这个正多边形的边数为（）

A、10 B、11 C、12 D、13

查看试题解析
5. 有9名同学参加歌咏比赛，他们的预赛成绩各不相同，现取其中前4名参加决赛，小红同学知道自己的成绩后，要判断能否进入决赛，还需知道这9名同学成绩的（　　）

A、众数 B、中位数 C、平均数 D、方差

查看试题解析
6. 如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是（）

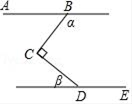A、α+β＝180° B、α+β＝90° C、β＝3α D、α﹣β＝90°

查看试题解析
7. 如图， $▱$ $A B C D$ 的对角线AC，BD相交于点O， $E$ 是AB中点，且AE+EO=4，则 $▱ A B C D$ 的周长为（）

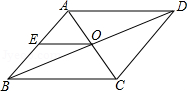A、20 B、16 C、12 D、8

查看试题解析
8. 关于 $x$ 的一元二次方程 $(k + 1) x^{2} - 2 x + 1 = 0$ 有两个实数根，则 $k$ 的取值范围是（）

A、k≥0 B、k≤0 C、k＜0且 $k \neq - 1$ D、k≤0且 $k \neq - 1$

查看试题解析
9. 在同平面直角坐标系中，函数y＝x﹣1与函数y＝ $\frac{1}{x}$ 的图象大致是（　　）

A、 B、 C、 D、

查看试题解析
10. 如图，CE是□ABCD的边AB的垂直平分线，垂足为点O ， CE与DA的延长线交于点E、连接AC ， BE ， DO ， DO与AC交于点F ，则下列结论：①四边形ACBE是菱形；②∠ACD＝∠BAE；③AF：BE＝2：3；④S_四边形_AFOE：S_△_COD＝2：3．其中正确的结论有（　　）个．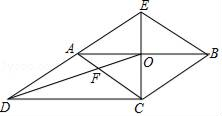

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 分解因式：ab²﹣9a= ．

查看试题解析
12. 若x²﹣2x＝1，则2x²﹣4x+3＝．

查看试题解析
13. 如下图，在Rt△ABC中，∠C=90°，DE垂直平分AB，垂足为E，D在BC上，已知∠CAD=32°，则∠B=度．

查看试题解析
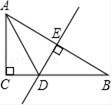14. 对于实数a，b，定义运算“※”如下：a※b=a²﹣ab，例如，5※3=5²﹣5×3=10．若（x+1）※（x﹣2）=6，则x的值为．

查看试题解析
15. 如图，点 A 在双曲线y＝ $\frac{5}{x}$ 上，点 B 在双曲线y＝ $\frac{8}{x}$ 上，且AB∥x轴，则△OAB 的面积等于．

查看试题解析
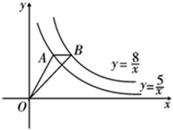16. 如图，在平面直角坐标系中，等腰直角三角形OAA₁的直角边OA在x轴上，点A₁在第一象限，且OA=1，以点A₁为直角顶点，OA₁为一直角边作等腰直角三角形OA₁A₂ ，再以点A₂为直角顶点，OA₂为直角边作等腰直角三角形OA₂A₃…依此规律，则点A₂₀₁₈的坐标是．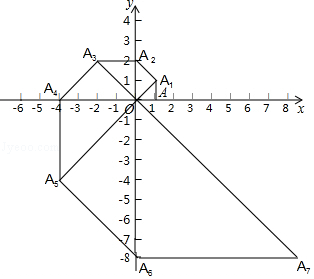

查看试题解析

三、解答题

17. 解分式方程： $\frac{x}{x - 1}$ + $\frac{2}{1 - x}$ =4．

查看试题解析
18. 先化简，再求值：（1﹣ $\frac{1}{a + 1}$ ）÷ $\frac{2 a}{a^{2} - 1}$ ，其中a＝﹣2．

查看试题解析
19. 如图，在△ABC中，∠C＝90°，∠B＝30°

(1)、在BC上作出点D ，使它到A ， B两点的距离相等（用尺规作图法，保留作图痕迹，不要求写作法）

(2)、若BD＝6，求CD长．

查看试题解析
20. 为进一步推广“阳光体育”大课间活动，某中学对已开设的A实心球，B立定跳远，C跑步，D跳绳四种活动项目的学生喜欢情况进行调查，随机抽取了部分学生，并将调查结果绘制成图1，图2的统计图，请结合图中的信息解答下列问题：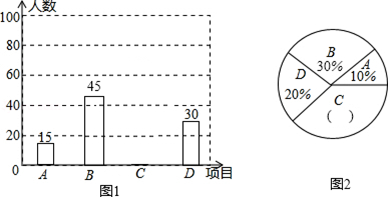

(1)、请计算本次调查中喜欢“跑步”的学生人数和所占百分比，并将两个统计图补充完整；

(2)、随机抽取了5名喜欢“跑步”的学生，其中有3名女生，2名男生，现从这5名学生中任意抽取2名学生，请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．

查看试题解析
21. 郴州市正在创建“全国文明城市”，某校拟举办“创文知识”抢答赛，欲购买A、B两种奖品以鼓励抢答者．如果购买A种20件，B种15件，共需380元；如果购买A种15件，B种10件，共需280元．

(1)、A、B两种奖品每件各多少元？

(2)、现要购买A、B两种奖品共100件，总费用不超过900元，那么A种奖品最多购买多少件？

查看试题解析
22. 已知：如图，在△ABC中，∠BAC=90°，M是斜边BC的中点，BN⊥AM ，垂足为点N ，且BN的延长线交AC于点D ．

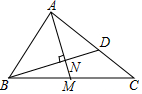(1)、求证：△ABC∽△ADB；

(2)、如果BC=20，BD=15，求AB的长度．

查看试题解析
23. 如图，在平行四边形ABCD中，过对角线BD中点的直线交AD、BC边于F、E ．

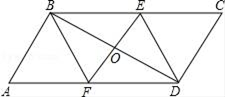(1)、求证：四边形BEDF是平行四边形；

(2)、当四边形BEDF是菱形时，写出EF与BD的关系．

(3)、若∠A＝60°，AB＝4，BC＝6，四边形BEDF是矩形，求该矩形的面积．

查看试题解析
24. 如图1，直线y＝k₁x+b与反比例函数y＝ $\frac{k_{2}}{x}$ 的图象交于A（1，6），B（a ， 3）两点．

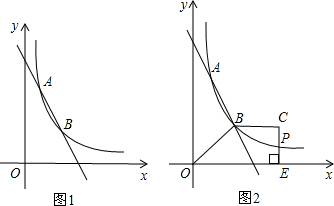(1)、求k₁、k₂的值；

(2)、结合图形，在第一象限内，直接写出k₁x+b﹣ $\frac{k_{2}}{x}$ ＞0时，x的取值范围；

(3)、如图2，梯形OBCE中，BC∥OE ，过点C作CE⊥x轴于点E ， CE和反比例函数的图象交于点P ，当梯形OBCE的面积为9时，请判断PC和PE的大小关系，并说明理由．

查看试题解析
25. 在平面直角坐标系中，四边形AOBC是矩形，点O（0，0），点A（5，0），点B（0，3）．以点A为中心，顺时针旋转矩形AOBC ，得到矩形ADEF ，点O ， B ， C的对应点分别为D ， E ， F ．

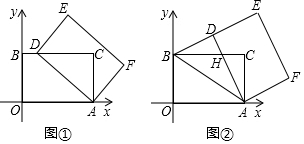(1)、如图①，当点D落在BC边上时，求点D的坐标；

(2)、如图②，当点D落在线段BE上时，AD与BC交于点H ．
①求证△ADB≌△AOB；

②求点H的坐标．

(3)、记K为矩形AOBC对角线的交点，S为△KDE的面积，求S的取值范围（直接写出结果即可）．

查看试题解析