广东省2018-2019学年中考数学模拟考试试卷
试卷更新日期:2019-06-04 类型:中考模拟
一、单选题
-
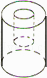
1. 的相反数是A、2 B、 C、 D、2. 据统计,2017年河南省的夏粮收购总产量为796.24亿斤,请用科学记数法表示这个数为( )A、7.9624×1010 B、7.9624×109 C、79.624×109 D、0.79624×10113. 如图,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 一个袋子中装有3个红球和2个黄球,这些球的形状、大小.质地完全相同,在看不到球的条件下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是( )A、 B、 C、 D、5. 下面的图形中,既是轴对称图形又是中心对称图形的是( )
4. 一个袋子中装有3个红球和2个黄球,这些球的形状、大小.质地完全相同,在看不到球的条件下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是( )A、 B、 C、 D、5. 下面的图形中,既是轴对称图形又是中心对称图形的是( )
A、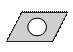 B、
B、 C、
C、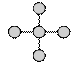 D、
D、 6. 某同学做了四道题:①3m+4n=7mn;②(﹣2a2)3=﹣8a6;③6x6÷2x2=3x3;④y3•xy2=xy5 , 其中正确的题号是( )A、②④ B、①③ C、①② D、③④7. 如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
6. 某同学做了四道题:①3m+4n=7mn;②(﹣2a2)3=﹣8a6;③6x6÷2x2=3x3;④y3•xy2=xy5 , 其中正确的题号是( )A、②④ B、①③ C、①② D、③④7. 如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( ) A、100° B、90° C、80° D、70°8. 如图,双曲线y= (x>0)经过线段AB的中点M,则△AOB的面积为( )
A、100° B、90° C、80° D、70°8. 如图,双曲线y= (x>0)经过线段AB的中点M,则△AOB的面积为( )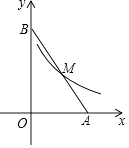 A、18 B、24 C、6 D、129. 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
A、18 B、24 C、6 D、129. 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )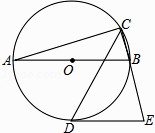 A、 B、2 C、2 D、310.
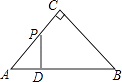
A、 B、2 C、2 D、310.如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A﹣C﹣B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )
 A、
A、 B、
B、 C、
C、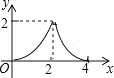 D、
D、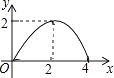
二、填空题
-
11. 分解因式:ma2﹣4ma+4m= .12. 若关于x的一元二次方程x2+2x﹣k=0没有实数根,则k的取值范围是 .13. 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于 .
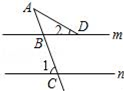 14. 如图,在▱ABCD中,E为AD的三等分点,AE= AD,连接BE交AC于点F,AC=12,则AF为 .
14. 如图,在▱ABCD中,E为AD的三等分点,AE= AD,连接BE交AC于点F,AC=12,则AF为 .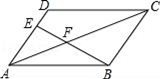 15. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作 交AB于点E,以点B为圆心,BC的长为半径作 交AB于点D,则阴影部分的面积为 .
15. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作 交AB于点E,以点B为圆心,BC的长为半径作 交AB于点D,则阴影部分的面积为 .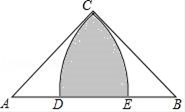
三、解答题
-
16. 计算:( )﹣2+(π﹣2019)0+sin60°+| ﹣2|17. 先化简,再求值:( )÷ ,其中实数a,b满足(a﹣2)2+|b﹣2a|=0.18. 如图,△ABC是直角三角形,∠ACB=90°.
 (1)、尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.
(1)、尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.
(2)、在你按(1)中要求所作的图中,若BC=3,∠A=30°,求 的长.
19. 甲、乙两同学从家到学校的距离之比是10:7,甲同学的家与学校的距离为3000米,甲同学乘公交车去学校、乙同学骑自行车去学校.已知公交车速度是乙骑自行车速度的2倍,甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.(1)、求乙同学的家与学校的距离为多少米?(2)、求乙骑自行车的速度.20. 某校为了了解学生在家使用电脑的情况(分为“总是、较多、较少、不用”四种情况),随机在八、九年级各抽取相同数量的学生进行调查,绘制成部分统计图如下所示.请根据图中信息,回答下列问题: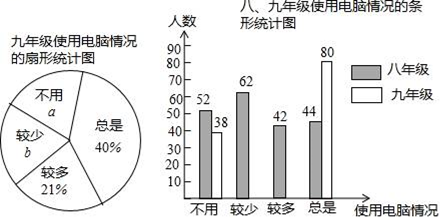 (1)、九年级一共抽查了多少名学生,图中的a等于多少,“总是”对应的圆心角为多少度.(2)、根据提供的信息,补全条形统计图.(3)、若该校九年级共有900名学生,请你统计其中使用电脑情况为“较少”的学生有多少名?21. 某数学活动小组实地测量湛河两岸互相平行的一段东西走向的河的宽度,在河的北岸边点A处,测得河的南岸边点B处在其南偏东45°方向,然后向北走20米到达点C处,测得点B在点C的南偏东33°方向,请求出这段河的宽度.(结果精确到1米.参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65, ≈1.41)
(1)、九年级一共抽查了多少名学生,图中的a等于多少,“总是”对应的圆心角为多少度.(2)、根据提供的信息,补全条形统计图.(3)、若该校九年级共有900名学生,请你统计其中使用电脑情况为“较少”的学生有多少名?21. 某数学活动小组实地测量湛河两岸互相平行的一段东西走向的河的宽度,在河的北岸边点A处,测得河的南岸边点B处在其南偏东45°方向,然后向北走20米到达点C处,测得点B在点C的南偏东33°方向,请求出这段河的宽度.(结果精确到1米.参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65, ≈1.41)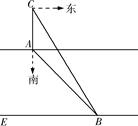 22. 如图,直线L:y=- x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
22. 如图,直线L:y=- x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.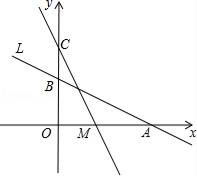 (1)、求A、B两点的坐标;(2)、求△COM的面积S与M的移动时间t之间的函数关系式;(3)、当t为何值时△COM≌△AOB,并求此时M点的坐标.23. 如图在⊙O中,BC=2,AB=AC,点D为AC上的动点,且cosB= .
(1)、求A、B两点的坐标;(2)、求△COM的面积S与M的移动时间t之间的函数关系式;(3)、当t为何值时△COM≌△AOB,并求此时M点的坐标.23. 如图在⊙O中,BC=2,AB=AC,点D为AC上的动点,且cosB= . (1)、求AB的长度;(2)、求AD•AE的值;(3)、过A点作AH⊥BD,求证:BH=CD+DH.24. 如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)、求AB的长度;(2)、求AD•AE的值;(3)、过A点作AH⊥BD,求证:BH=CD+DH.24. 如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.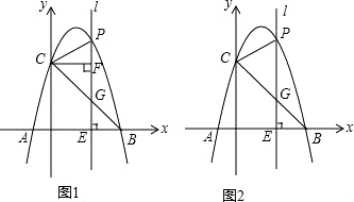 (1)、求抛物线的表达式;(2)、当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;(3)、如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
(1)、求抛物线的表达式;(2)、当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;(3)、如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.