北京市通州区2018-2019学年中考数学一模考试试卷
试卷更新日期:2019-06-04 类型:中考模拟
一、单选题
-
1. 如图所示,用直尺度量线段AB,可以读出AB的长度为( )
 A、6cm B、7cm C、8cm D、9cm2. 实数a,b,c,d在数轴上的对应点的位置如图所示,则这四个数中,相反数是正数的为( )
A、6cm B、7cm C、8cm D、9cm2. 实数a,b,c,d在数轴上的对应点的位置如图所示,则这四个数中,相反数是正数的为( )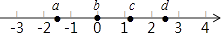 A、a B、b C、c D、d3. 北京城市副中心生态文明建设在2016年取得突出成果,通过大力推进能源结构调整,热电替代供热面积为17960000平方米.将17960000用科学记数法表示应为( )A、1.796×106 B、17.96×106 C、1.796×107 D、0.1796×1074. 如图是某个几何体的三视图,该几何体是( )
A、a B、b C、c D、d3. 北京城市副中心生态文明建设在2016年取得突出成果,通过大力推进能源结构调整,热电替代供热面积为17960000平方米.将17960000用科学记数法表示应为( )A、1.796×106 B、17.96×106 C、1.796×107 D、0.1796×1074. 如图是某个几何体的三视图,该几何体是( )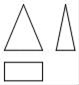 A、圆锥 B、四棱锥 C、圆柱 D、四棱柱5. 下列图形中,是中心对称图形的是( )A、
A、圆锥 B、四棱锥 C、圆柱 D、四棱柱5. 下列图形中,是中心对称图形的是( )A、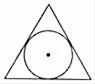 B、
B、 C、
C、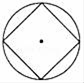 D、
D、 6. 如果a+b= ,那么 的值是( )A、 B、 C、2 D、47. 如图,在平面直角坐标系xOy中,点A,B,C满足二次函数y=ax2+bx的表达式,则对该二次函数的系数a和b判断正确的是( )
6. 如果a+b= ,那么 的值是( )A、 B、 C、2 D、47. 如图,在平面直角坐标系xOy中,点A,B,C满足二次函数y=ax2+bx的表达式,则对该二次函数的系数a和b判断正确的是( )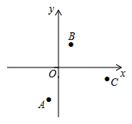 A、a>0,b>0 B、a<0,b<0 C、a>0,b<0 D、a<0,b>08. 如图,将一张矩形的纸对折,旋转90°后再对折,然后沿着下图中的虚线剪下,则剪下的纸片打开后的形状一定为( )
A、a>0,b>0 B、a<0,b<0 C、a>0,b<0 D、a<0,b>08. 如图,将一张矩形的纸对折,旋转90°后再对折,然后沿着下图中的虚线剪下,则剪下的纸片打开后的形状一定为( ) A、三角形 B、菱形 C、矩形 D、正方形9. 如图,在平面直角坐标系xO1y中,点A的坐标为(1,1).如果将x轴向上平移3个单位长度,将y轴向左平移2个单位长度,交于点O2 , 点A的位置不变,那么在平面直角坐标系xO2y中,点A的坐标是( )
A、三角形 B、菱形 C、矩形 D、正方形9. 如图,在平面直角坐标系xO1y中,点A的坐标为(1,1).如果将x轴向上平移3个单位长度,将y轴向左平移2个单位长度,交于点O2 , 点A的位置不变,那么在平面直角坐标系xO2y中,点A的坐标是( ) A、(3,﹣2) B、(﹣3,2) C、(﹣2,﹣3) D、(3,4)10. 小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
A、(3,﹣2) B、(﹣3,2) C、(﹣2,﹣3) D、(3,4)10. 小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )①小亮测试成绩的平均数比小明的高;②小亮测试成绩比小明的稳定;③小亮测试成绩的中位数比小明的高;④小亮参加第一轮比赛,小明参加第二轮比赛,比较合理.
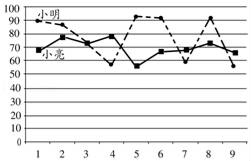 A、①③ B、①④ C、②③ D、②④
A、①③ B、①④ C、②③ D、②④二、填空题
-
11. 函数y= 的自变量x的取值范围是 .12. 如图,正方形ABCD由四个矩形构成,根据图形,写出一个含有a和b的正确的等式 .
 13. 某农场引进一批新麦种,在播种前做了五次发芽实验,每次任取800 粒麦种进行实验.实验结果如表所示 ( 发芽率精确到 0.001 ):
13. 某农场引进一批新麦种,在播种前做了五次发芽实验,每次任取800 粒麦种进行实验.实验结果如表所示 ( 发芽率精确到 0.001 ):实验的麦种数
800
800
800
800
800
发芽的麦种数
787
779
786
789
782
发芽率
0.984
0.974
0.983
0.986
0.978
在与实验条件相同的情况下,估计种一粒这样的麦种发芽的概率为 .
14. 如图所示,某地三条互相平行的街道a,b,c与两条公路相交,有六个路口分别为A,B,C,D,E,F.路段EF正在封闭施工.若已知路段AB约为270.1米,路段BC约为539.8米,路段DE约为282.0米,则封闭施工的路段EF的长约为米.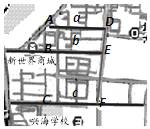 15. 古代有这样一个数学问题:韩信点一队士兵人数,三人一组余两人,五人一组余三人,七人一组余四人.问这队士兵至少多少人?我国古代学者早就研究过这个问题.例如明朝数学家程大位在他著的《算法统宗》中就用四句口诀暗示了此题的解法:三人同行七十稀,五树梅花甘一枝,七子团圆正半,除百零五便得知.这四句口诀暗示的意思是:当除数分别是3,5,7时,用70乘以用3除的余数(例如:韩信点兵问题中用70乘以2),用21乘以用5除的余数,用15乘以用7除的余数,然后把三个乘积相加.加得的结果如果比105大就除以105,所得的余数就是满足题目要求的最小正整数解.按这四句口诀暗示的方法计算韩信点的这队士兵的人数为 .16. 工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC即是∠AOB的平分线.这种做法的依据是 .
15. 古代有这样一个数学问题:韩信点一队士兵人数,三人一组余两人,五人一组余三人,七人一组余四人.问这队士兵至少多少人?我国古代学者早就研究过这个问题.例如明朝数学家程大位在他著的《算法统宗》中就用四句口诀暗示了此题的解法:三人同行七十稀,五树梅花甘一枝,七子团圆正半,除百零五便得知.这四句口诀暗示的意思是:当除数分别是3,5,7时,用70乘以用3除的余数(例如:韩信点兵问题中用70乘以2),用21乘以用5除的余数,用15乘以用7除的余数,然后把三个乘积相加.加得的结果如果比105大就除以105,所得的余数就是满足题目要求的最小正整数解.按这四句口诀暗示的方法计算韩信点的这队士兵的人数为 .16. 工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC即是∠AOB的平分线.这种做法的依据是 .
三、解答题
-
17. 计算: +|1﹣ |﹣2cos45°+( )﹣1 .18. 解不等式组:19. 如图,在矩形ABCD中,连接对角线AC,BD,延长BC至点E,使BC=CE,连接DE.
求证:DE=AC.
 20. 在平面直角坐标系xOy中,过原点O的直线l1与双曲线 的一个交点为A(1,m).(1)、求直线l1的表达式;(2)、过动点P(n,0)(n>0)且垂直于x轴的直线与直线l1和双曲线 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.21. 关于x的一元二次方程x2﹣2mx+(m﹣1)2=0有两个相等的实数根.
20. 在平面直角坐标系xOy中,过原点O的直线l1与双曲线 的一个交点为A(1,m).(1)、求直线l1的表达式;(2)、过动点P(n,0)(n>0)且垂直于x轴的直线与直线l1和双曲线 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.21. 关于x的一元二次方程x2﹣2mx+(m﹣1)2=0有两个相等的实数根.(Ⅰ)求m的值;
(II)求此方程的根.
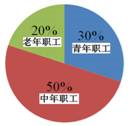
22. 某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄
26
42
57
健康指数
97
79
72
表2:小王抽样调查单位10名职工的健康指数
年龄
23
25
26
32
33
37
39
42
48
52
健康指数
93
89
90
83
79
75
80
69
68
60
表3:小李抽样调查单位10名职工的健康指数
年龄
22
29
31
36
39
40
43
46
51
55
健康指数
94
90
88
85
82
78
72
76
62
60
根据上述材料回答问题:
小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
 23. 如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
23. 如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB. (1)、求证:四边形DBFC是平行四边形;(2)、如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.24. 如图,点C在以AB为直径的⊙O上,BD与过点C的切线垂直于点D,BD与⊙O交于点E.
(1)、求证:四边形DBFC是平行四边形;(2)、如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.24. 如图,点C在以AB为直径的⊙O上,BD与过点C的切线垂直于点D,BD与⊙O交于点E.
(1)、求证:BC平分∠DBA;(2)、连接AE和AC,若cos∠ABD= ,OA=m,请写出求四边形AEDC面积的思路.
25. 阅读下列材料:环视当今世界,科技创新已成为发达国家保持持久竞争力的“法宝”.研究与试验发展(R&D)活动的规模和强度指标反映一个地区的科技实力和核心竞争力.
北京市在研究和实验发展(R&D)活动中的经费投入也在逐年增加.2012年北京市全年研究与试验发展(R&D)经费投入1031.1亿元,比上年增长10.1%.2013年全年研究与试验发展(R&D)经费投入1200.7亿元.2014年全年研究与试验发展(R&D)经费投入1286.6亿元.2015年研究与试验发展(R&D)经费投入1367.5亿元.2016年研究与试验发展(R&D)经费投入1479.8亿元,相当于地区生产总值的5.94%.
(以上数据来源于北京市统计局)
根据以上材料解答下列问题:
(1)、用折线统计图或者条形统计图将2012﹣2016年北京市在研究和实验发展(R&D)活动中的经费投入表示出来,并在图中标明相应数据;(2)、根据绘制的统计图提供的信息,预估2017年北京市在研究和实验发展(R&D)活动中的经费投入约为多少亿元,写出你的预估理由.26. 已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.x
…
1
2
4
5
6
8
9
…
y
…
3.92
1.95
0.98
0.78
2.44
2.44
0.78
…
小风根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象和性质进行了探究.
下面是小风的探究过程,请补充完整:
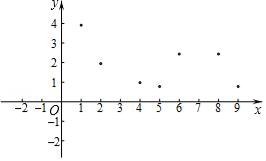
(1)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(2)、根据画出的函数图象,写出:①x=7对应的函数值y约为多少;
②写出该函数的一条性质.
 27. 在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-m+2的顶点为D.线段AB的两个端点分别为A(-3,m),B(1,m).(1)、求点D的坐标(用含m的代数式表示);(2)、若该抛物线经过点B(1,m),求m的值;(3)、若线段AB与该抛物线只有一个公共点,结合函数的图象,求m的取值范围.28. 在等边三角形ABC中,E为直线AB上一点,连接EC.ED与直线BC交于点D,ED=EC.
27. 在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-m+2的顶点为D.线段AB的两个端点分别为A(-3,m),B(1,m).(1)、求点D的坐标(用含m的代数式表示);(2)、若该抛物线经过点B(1,m),求m的值;(3)、若线段AB与该抛物线只有一个公共点,结合函数的图象,求m的取值范围.28. 在等边三角形ABC中,E为直线AB上一点,连接EC.ED与直线BC交于点D,ED=EC. (1)、如图1,AB=1,点E是AB的中点,求BD的长;(2)、点E是AB边上任意一点(不与AB边的中点和端点重合),依题意,将图2补全,判断AE与BD间的数量关系并证明;(3)、点E不在线段AB上,请在图3中画出符合条件的一个图形.29. 在平面直角坐标系xOy中,点A(x1 , y1),B(x2 , y2),若x1x2+y1y2=0,且A,B均不为原点,则称A和B互为正交点.比如:A(1,1),B(2,﹣2),其中1×2+1×(﹣2)=0,那么A和B互为正交点.(1)、点P和Q互为正交点,P的坐标为(﹣2,3),
(1)、如图1,AB=1,点E是AB的中点,求BD的长;(2)、点E是AB边上任意一点(不与AB边的中点和端点重合),依题意,将图2补全,判断AE与BD间的数量关系并证明;(3)、点E不在线段AB上,请在图3中画出符合条件的一个图形.29. 在平面直角坐标系xOy中,点A(x1 , y1),B(x2 , y2),若x1x2+y1y2=0,且A,B均不为原点,则称A和B互为正交点.比如:A(1,1),B(2,﹣2),其中1×2+1×(﹣2)=0,那么A和B互为正交点.(1)、点P和Q互为正交点,P的坐标为(﹣2,3),①如果Q的坐标为(6,m),那么m的值为多少;
②如果Q的坐标为(x,y),求y与x之间的关系式;
(2)、点M和N互为正交点,直接写出∠MON的度数;(3)、点C,D是以(0,2)为圆心,半径为2的圆上的正交点,以线段CD为边,构造正方形CDEF,圆心F在正方形CDEF的外部,求线段OE长度的取值范围.