2016-2017学年湖北省鄂州市九年级下学期期中数学试卷

试卷更新日期：2017-05-25 类型：期中考试

进入出卷网下载

一、选择题

1. |﹣8|的相反数是（）

A、﹣8 B、8 C、 $\frac{1}{8}$ D、﹣ $\frac{1}{8}$

查看试题解析
2. 下列运算正确的是（）

A、a³•a⁴=a¹² B、3a²•2a³=6a⁶ C、（﹣2x²y）³=﹣8x⁶y³ D、（﹣3a²b³）²=6a⁴b⁶

查看试题解析
3. 下图是一个由多个相同小正方体堆积而成的几何体的俯视图，图中所示数字为该位置小正方体的个数，则这个几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 阿联抛一枚质地均匀的硬币，连续抛3次，硬币均正面朝上落地，如果他再抛第4次，那么硬币正面朝上的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、1

查看试题解析
5. 若方程组 ${\begin{cases} 3 x + y = k + 1 \\ x + 3 y = 3 \end{cases}$ 的解x，y满足0＜x+y＜1，则k的取值范围是（）

A、﹣4＜k＜0 B、﹣1＜k＜0 C、0＜k＜8 D、k＞﹣4

查看试题解析
6.
如图，△ABC中，D、E分别是BC、AC的中点，BF平分∠ABC，交DE于点F，若BC=6，则DF的长是（　　）

A、3 B、2 C、 $\frac{5}{2}$ D、4

查看试题解析
7. 如图所示，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y= $\frac{k}{x}$ （k≠0）在第一象限的图象经过顶点A（m，m+3）和CD上的点E，且OB﹣CE=1．直线l过O、E两点，则tan∠EOC的值为（）

A、 $\frac{9}{2}$ B、5 C、 $\frac{2}{9}$ D、3

查看试题解析
8. 如图，AB是⊙O的直径，BD、CD分别是过⊙O上点B、C的切线，且∠BDC=100°，连接AC，则∠A的度数是（）

A、15° B、30° C、40° D、45°

查看试题解析
9. 如图是二次函数y=ax²+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：
①abc＜0；
②2a﹣b=0；
③4a+2b+c＜0；
④若（﹣5，y₁），（ $\frac{5}{2}$ ，y₂）是抛物线上两点，则y₁＞y₂ ．
其中说法正确的是（）

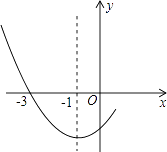A、①② B、②③ C、①②④ D、②③④

查看试题解析
10. 如图，P为⊙O内的一个定点，A为⊙O上的一个动点，射线AP、AO分别与⊙O交于B、C两点．若⊙O的半径长为3，OP= $\sqrt{3}$ ，则弦BC的最大值为（）

A、2 $\sqrt{3}$ B、3 C、 $\sqrt{6}$ D、3 $\sqrt{2}$

查看试题解析

二、填空题

11. 分解因式：（a²+1）²﹣4a²= ．

查看试题解析
12. 若一元二次方程ax²=b（ab＞0）的两个根分别是m+2与2m﹣5，则 $\frac{b}{a}$ = ．

查看试题解析
13. 在△ABC中，∠C=90°，AB=6，sin∠B= $\frac{1}{3}$ ，则BC= ．

查看试题解析
14. 将△ABC的纸片按如图所示的方式折叠，使点B落在边AC上，记为点B′，折叠痕为EF，已知AB=AC=8，BC=10，若以点B′、F、C为顶点的三角形与△ABC相似，那么BF的长度是．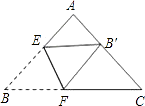

查看试题解析
15. 如图，在正方形ABCD内有一折线段，其中AE丄EF，EF丄FC，并且AE=3，EF=4，FC=5，则正方形ABCD的外接圆的半径是．

查看试题解析
16.
如图①，在正方形ABCD中，点P沿边DA从点D开始向点A以1cm/s的速度移动；同时，点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动．当点P移动到点A时，P、Q同时停止移动．设点P出发xs时，△PAQ的面积为ycm² ， y与x的函数图象如图②，则线段EF所在的直线对应的函数关系式为．

查看试题解析

三、简答题

17. 先化简，再求值：（ $\frac{x - 1}{x^{2} - x}$ ﹣ $\frac{x}{x^{2} - 2 x + 1}$ ）÷ $\frac{1}{x - 1}$ ，其中x满足方程x²﹣x﹣6=0．

查看试题解析
18. 在四张编号为A，B，C，D的卡片（除编号外，其余完全相同）的正面分别写上如图所示正整数后，背面朝上，洗匀放好，现从中随机抽取一张（不放回），再从剩下的卡片中随机抽取一张．

(1)、请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果（卡片用A，B，C，D表示）；

(2)、我们知道，满足a²+b²=c²的三个正整数a，b，c成为勾股数，求抽到的两张卡片上的数都是勾股数的概率．

查看试题解析
19. 已知关于x的一元二次方程x²﹣（2k+1）x+k²+2k=0有两个实数根x₁ ， x₂ ．

(1)、求实数k的取值范围；

(2)、是否存在实数k使得x₁•x₂﹣x₁²﹣x₂²≥0成立？若存在，请求出k的值；若不存在，请说明理由．

查看试题解析
20. 如图，已知在△ABC中，AD平分∠BAC，EM是AD的中垂线，交BC延长线于E．

(1)、连接AE，证明：∠EAC=∠B．

(2)、求证：DE²=BE•CE．

查看试题解析
21.
如图，已知斜坡AB长为80米，坡角（即∠BAC）为30°，BC⊥AC，现计划在斜坡中点D处挖去部分坡体（用阴影表示）修建一个平行于水平线CA的平台DE和一条新的斜坡BE．

(1)、若修建的斜坡BE的坡角为45°，求平台DE的长；（结果保留根号）

(2)、一座建筑物GH距离A处36米远（即AG为36米），小明在D处测得建筑物顶部H的仰角（即∠HDM）为30°．点B、C、A、G、H在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，求建筑物GH的高度．（结果保留根号）

查看试题解析
22. 如图，已知Rt△ABC，∠ABC=90°，以直角边AB为直径作⊙O，交斜边AC于点D，连接BD．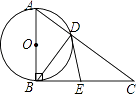

(1)、若AD=3，BD=4，求边BC的长；

(2)、取BC的中点E，连接ED，试证明ED与⊙O相切．

查看试题解析
23. 某公司投资1200万元购买了一条新生产线生产新产品．根据市场调研，生产每件产品需要成本50元，该产品进入市场后不得低于80元/件且不得超过160元/件，该产品销售量y（万件）与产品售价x（元）之间的关系如图所示．

(1)、求y与x之间的函数关系式，并写出x的取值范围；

(2)、第一年公司是盈利还是亏损？求出当盈利最大或亏损最小时的产品售价；

(3)、在（2）的前提下，即在第一年盈利最大或者亏损最小时，公司第二年重新确定产品售价，能否使前两年盈利总额达790万元？若能，求出第二年产品售价；若不能，说明理由．

查看试题解析
24.
已知：如图一，抛物线y=ax²+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y=x﹣2经过A、C两点，且AB=2．

(1)、求抛物线的解析式；

(2)、
若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移，且分别交y轴、线段BC于点E，D，同时动点P从点B出发，沿BO方向以每秒2个单位速度运动，（如图2）；当点P运动到原点O时，直线DE与点P都停止运动，连DP，若点P运动时间为t秒；设s= $\frac{E D + O P}{E D \cdot O P}$ ，当t为何值时，s有最小值，并求出最小值．

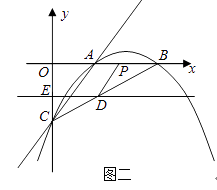(3)、在（2）的条件下，是否存在t的值，使以P、B、D为顶点的三角形与△ABC相似；若存在，求t的值；若不存在，请说明理由．

查看试题解析