2016-2017学年江苏省无锡市江阴市青阳片九年级下学期期中数学试卷
试卷更新日期:2017-05-25 类型:期中考试
一、选择题
-
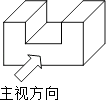
1. 如果a与﹣3互为相反数,则a等于( )A、 B、3 C、﹣ D、﹣32. 下列各式运算中,正确的是( )A、(a+b)2=a2+b2 B、 C、a3•a4=a12 D、3. 下列调查方式中适合的是( )A、要了解一批节能灯的使用寿命,采用普查方式 B、调查你所在班级同学的身高,采用抽样调查方式 C、环保部门调查沱江某段水域的水质情况,采用抽样调查方式 D、调查全市中学生每天的就寝时间,采用普查方式4. 图中所示几何体的俯视图是( )
 A、
A、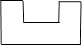 B、
B、 C、
C、 D、
D、 5. 如图,AB∥CD,则根据图中标注的角,下列关系中成立的是( )
5. 如图,AB∥CD,则根据图中标注的角,下列关系中成立的是( ) A、∠1=∠3 B、∠2+∠3=180° C、∠2+∠4<180° D、∠3+∠5=180°6. 关于抛物线y=(x﹣1)2+2,下列结论中不正确是( )A、对称轴为直线x=1 B、当x<1时,y随x的增大而减小 C、与x轴没有交点 D、与y轴交于点(0,2)7. 晓明家到学校的路程是3500米,晓明每天早上7:30离家步行去上学,在8:10(含8:10)至8:20(含8:20)之间到达学校.如果设晓明步行的速度为x米/分,则晓明步行的速度范围是( )A、70≤x≤87.5 B、x≤70或x≥87.5 C、x≤70 D、x≥87.58. 如图,已知菱形OABC的顶点O(0,0),B(﹣2,﹣2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
A、∠1=∠3 B、∠2+∠3=180° C、∠2+∠4<180° D、∠3+∠5=180°6. 关于抛物线y=(x﹣1)2+2,下列结论中不正确是( )A、对称轴为直线x=1 B、当x<1时,y随x的增大而减小 C、与x轴没有交点 D、与y轴交于点(0,2)7. 晓明家到学校的路程是3500米,晓明每天早上7:30离家步行去上学,在8:10(含8:10)至8:20(含8:20)之间到达学校.如果设晓明步行的速度为x米/分,则晓明步行的速度范围是( )A、70≤x≤87.5 B、x≤70或x≥87.5 C、x≤70 D、x≥87.58. 如图,已知菱形OABC的顶点O(0,0),B(﹣2,﹣2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( ) A、(1,﹣1) B、(﹣1,﹣1) C、(1,1) D、(﹣1,1)9. 当m,n是实数且满足m﹣n=mn时,就称点Q(m, )为“奇异点”,已知点A、点B是“奇异点”且都在反比例函数y= 的图象上,点O是平面直角坐标系原点,则△OAB的面积为( )A、1 B、 C、2 D、
A、(1,﹣1) B、(﹣1,﹣1) C、(1,1) D、(﹣1,1)9. 当m,n是实数且满足m﹣n=mn时,就称点Q(m, )为“奇异点”,已知点A、点B是“奇异点”且都在反比例函数y= 的图象上,点O是平面直角坐标系原点,则△OAB的面积为( )A、1 B、 C、2 D、二、填空题
-
10. 分解因式:a2﹣4a+4= .11. 据媒体报道,我国因环境污染造成的巨大经济损失,每年高达680000000元,这个数用科学记数法表示为元.12. 若一个多边形的内角和比外角和大360°,则这个多边形的边数为 .13. 一组数据1,2,a,4,5的平均数是3,则这组数据的方差为 .14. 有一个正六面体,六个面上分别写有1~6这6个整数,投掷这个正六面体一次,向上一面的数字是2的倍数或3的倍数的概率是 .15. 如图,△ABC中,DE∥FG∥BC,AD:DF:FB=2:3:4,若EG=4,则AC= .
 16. 如图,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y= 的图象上,则k的值为 .
16. 如图,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y= 的图象上,则k的值为 . 17. 如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 .
17. 如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 .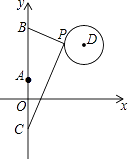
三、解答题
-
18. 计算:(1)、(﹣3)2﹣ +( )﹣1 .(2)、(x+1)2﹣2(x﹣2).19. 计算。(1)、解方程: +3=(2)、解不等式:2x﹣3≤ (x+2)20. 如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.
 21. 中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
21. 中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:成绩x/分
频数
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
n
80≤x<90
m
0.35
90≤x≤100
50
0.25
请根据所给信息,解答下列问题:
 (1)、m= , n=;(2)、请补全频数分布直方图;(3)、这次比赛成绩的中位数会落在分数段;(4)、若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?22. 本校有A、B两个餐厅,甲、乙两名学生各自随机选择其中一个餐厅用餐,请用列表或画树状图的方法解答:(1)、甲、乙两名学生在同一餐厅用餐的概率;(2)、甲、乙两名学生至少有一人在B餐厅的概率.23. 2008年5月12日四川汶川地区发生8.0级特大地震.举国上下通过各种方式表达爱心.某企业决定用p万元援助灾区n所学校,用于搭建帐篷和添置教学设备.根据各校不同的受灾情况,该企业捐款的分配方案是:所有学校得到的捐款数都相等,到第n所学校时捐款恰好分完,捐款的分配方法如下表所示.(其中p,n,a都是正整数)根据以上信息,解答下列问题:(1)、写出p与n的关系式;(2)、当p=125时,该企业能援助多少所学校?(3)、根据震区灾情,该企业计划再次提供不超过20a万元的捐款,按照原来的分配方案援助其它学校.若a由(2)确定,则再次提供的捐款最多又可以援助多少所学校?
(1)、m= , n=;(2)、请补全频数分布直方图;(3)、这次比赛成绩的中位数会落在分数段;(4)、若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?22. 本校有A、B两个餐厅,甲、乙两名学生各自随机选择其中一个餐厅用餐,请用列表或画树状图的方法解答:(1)、甲、乙两名学生在同一餐厅用餐的概率;(2)、甲、乙两名学生至少有一人在B餐厅的概率.23. 2008年5月12日四川汶川地区发生8.0级特大地震.举国上下通过各种方式表达爱心.某企业决定用p万元援助灾区n所学校,用于搭建帐篷和添置教学设备.根据各校不同的受灾情况,该企业捐款的分配方案是:所有学校得到的捐款数都相等,到第n所学校时捐款恰好分完,捐款的分配方法如下表所示.(其中p,n,a都是正整数)根据以上信息,解答下列问题:(1)、写出p与n的关系式;(2)、当p=125时,该企业能援助多少所学校?(3)、根据震区灾情,该企业计划再次提供不超过20a万元的捐款,按照原来的分配方案援助其它学校.若a由(2)确定,则再次提供的捐款最多又可以援助多少所学校?分配顺序
分配数额(单位:万元)
帐篷费用
教学设备费用
第1所学校
5
剩余款的
第2所学校
10
再剩余款的
第3所学校
15
再剩余款的
…
…
…
第(n﹣1)所学校
5(n﹣1)
再剩余款的
第n所学校
5n
0
24. 在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)).问题:
 (1)、求∠ABC的度数;(2)、求证:△AEB≌△ADC;(3)、△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).(4)、如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′,使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.25. 如图,已知二次函数y=ax2﹣2ax+c(a<0)的图象与x轴负半轴交于点A(﹣1,0),与y轴正半轴交于点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
(1)、求∠ABC的度数;(2)、求证:△AEB≌△ADC;(3)、△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).(4)、如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′,使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.25. 如图,已知二次函数y=ax2﹣2ax+c(a<0)的图象与x轴负半轴交于点A(﹣1,0),与y轴正半轴交于点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B. (1)、求一次函数解析式;(2)、求顶点P的坐标;(3)、平移直线AB使其过点P,如果点M在平移后的直线上,且 ,求点M坐标;(4)、设抛物线的对称轴交x轴于点E,连接AP交y轴于点D,若点Q、N分别为两线段PE、PD上的动点,连接QD、QN,请直接写出QD+QN的最小值.26. 阅读图1的情景对话,然后解答问题:
(1)、求一次函数解析式;(2)、求顶点P的坐标;(3)、平移直线AB使其过点P,如果点M在平移后的直线上,且 ,求点M坐标;(4)、设抛物线的对称轴交x轴于点E,连接AP交y轴于点D,若点Q、N分别为两线段PE、PD上的动点,连接QD、QN,请直接写出QD+QN的最小值.26. 阅读图1的情景对话,然后解答问题: (1)、根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是命题(填“真”或“假”)(2)、在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;(3)、如图2,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆 的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
(1)、根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是命题(填“真”或“假”)(2)、在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;(3)、如图2,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆 的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
27. 如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决. (1)、将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度;(2)、在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红.
(1)、将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度;(2)、在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红.