2016-2017学年江苏省无锡市江阴市华士片九年级下学期期中数学试卷
试卷更新日期:2017-05-25 类型:期中考试
一、选择题
-
1. 下列各数中,属于无理数的是( )A、( )0 B、 C、 D、2. 下列运算正确的是( )A、(﹣2x2)3=﹣8x6 B、(a3)2=a5 C、a3•(﹣a)2=﹣a5 D、(﹣x)2÷x=﹣x3. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,也称为可入肺颗粒物,它们含有大量的有毒、有害物质,对人体健康和大气环境质量有很大危害.0.0000025用科学记数法可表示为( )A、2.5×10﹣5 B、0.25×10﹣7 C、2.5×10﹣6 D、25×10﹣54. 不等式组 的解集在数轴上表示正确的是( )A、
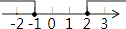 B、
B、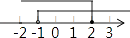 C、
C、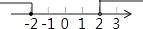 D、
D、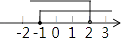 5. 若分式 的值为零,则x的值为( )A、0 B、1 C、﹣1 D、±16. 无锡市环保检测中心网站公布的2017年4月某日的PM2.5研究性检测部分数据如表:
5. 若分式 的值为零,则x的值为( )A、0 B、1 C、﹣1 D、±16. 无锡市环保检测中心网站公布的2017年4月某日的PM2.5研究性检测部分数据如表:时间
0:00
4:00
8:00
12:00
16:00
20:00
PM2.5(mg/m3)
0.027
0.035
0.032
0.014
0.016
0.032
则该日这6个时刻的PM2.5的众数和中位数分别是( )
A、0.032,0.0295 B、0.026,0.0295 C、0.026,0.032 D、0.032,0.0277. 已知如图抛物线y=ax2+bx+c,下列式子正确的是( ) A、a+b+c<0 B、b2﹣4ac<0 C、c<2b D、abc>08. 如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )
A、a+b+c<0 B、b2﹣4ac<0 C、c<2b D、abc>08. 如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( ) A、3 B、 C、4 D、9. 在△ABC中,AB=3,AC= .当∠B最大时,BC的长是( )A、 B、 C、 D、210. 如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1 , A2 , A3 , …,则A2015的坐标为.( )
A、3 B、 C、4 D、9. 在△ABC中,AB=3,AC= .当∠B最大时,BC的长是( )A、 B、 C、 D、210. 如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1 , A2 , A3 , …,则A2015的坐标为.( ) A、(1343,0) B、(1347,0) C、(1343 , ) D、(1347 , )
A、(1343,0) B、(1347,0) C、(1343 , ) D、(1347 , )二、填空题
-
11. 分解因式:2x2﹣18= .12. 要使式子 在实数范围内有意义,则x的取值范围是 .13. 已知一元二次方程x2+x﹣2=0,则方程的两根为 .14. 如果圆锥的底面半径为4cm,母线长为5cm,那么它的侧面积cm2 .15. 如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于°.
 16. 如图⊙O中,直径AB⊥弦CD于E,若AB=26,CD=24,则tan∠OCE= .
16. 如图⊙O中,直径AB⊥弦CD于E,若AB=26,CD=24,则tan∠OCE= . 17. 抛物线y=﹣ax2+bx+2,该抛物线的对称轴为直线x=1且过(﹣1,0),则抛物线的解析式为 .18. 如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5 千米的地方有一居民点B,A、B的直线距离是10 千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
17. 抛物线y=﹣ax2+bx+2,该抛物线的对称轴为直线x=1且过(﹣1,0),则抛物线的解析式为 .18. 如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5 千米的地方有一居民点B,A、B的直线距离是10 千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
三、解答题
-
19. 计算(1)、计算: +( )﹣1﹣2cos60°+(2﹣π)0;(2)、化简: .20. 计算(1)、解分式方程: + = ;(2)、解不等式组 .21. 初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
 (1)、在这次评价中,一共抽查了名学生;(2)、在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;(3)、请将频数分布直方图补充完整;(4)、如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人?22. 某市某幼儿园六一期间举行亲子游戏,主持人请三位家长分别带自己的孩子参加游戏,主持人准备把家长和孩子重新组合完成游戏,A、B、C分别表示三位家长,他们的孩子分别对应的是a、b、c.(1)、若主持人分别从三位家长和三位孩子中各选一人参加游戏,恰好是A、a的概率是多少(直接写出答案)(2)、若主持人先从三位家长中任选两人为一组,再从孩子中任选两人为一组,四人共同参加游戏,恰好是两对家庭成员的概率是多少.(画出树状图或列表)23. 已知:如图,▱ABCD中,CD=CB=2,∠C=60°,点E是CD边上自D向C的动点(点E运动到点C停止运动),连结AE,以AE为一边作等边△AEP,连结DP.
(1)、在这次评价中,一共抽查了名学生;(2)、在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;(3)、请将频数分布直方图补充完整;(4)、如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人?22. 某市某幼儿园六一期间举行亲子游戏,主持人请三位家长分别带自己的孩子参加游戏,主持人准备把家长和孩子重新组合完成游戏,A、B、C分别表示三位家长,他们的孩子分别对应的是a、b、c.(1)、若主持人分别从三位家长和三位孩子中各选一人参加游戏,恰好是A、a的概率是多少(直接写出答案)(2)、若主持人先从三位家长中任选两人为一组,再从孩子中任选两人为一组,四人共同参加游戏,恰好是两对家庭成员的概率是多少.(画出树状图或列表)23. 已知:如图,▱ABCD中,CD=CB=2,∠C=60°,点E是CD边上自D向C的动点(点E运动到点C停止运动),连结AE,以AE为一边作等边△AEP,连结DP. (1)、求证:△ABE≌△ADP;(2)、点P随点E的运动而运动,请直接写出点P的运动路径长 .24. 如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据 ≈1.41, ≈1.73)
(1)、求证:△ABE≌△ADP;(2)、点P随点E的运动而运动,请直接写出点P的运动路径长 .24. 如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据 ≈1.41, ≈1.73) 25. 做服装生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能售出A、B两种款式的服装合计30件,并且每售出一件A款式和B款式服装,甲店铺获利润分别为30元和35元,乙店铺获利润分别为26元和36元.某日,王老板进A款式服装36件,B款式服装24件,并将这批服装分配给两个店铺各30件.(1)、怎样将这60件服装分配给两个店铺,能使两个店铺在销售完这批服装后所获利润相同?(2)、怎样分配这60件服装能保证在甲店铺获利润不小于950元的前提下,王老板获利的总利润最大?最大的总利润是多少?26. 将一块a×b×c的长方体铁块(如图1所示,a<b<c,单位:cm)放入一长方体(如图2所示)水槽中,并以速度20cm3/s匀速向水槽注水,直至注满为止.若将铁块a×c面放至水槽的底面,则注水全过程中水槽的水深y (cm)与注水时间t (s)的函数图象如图3所示(水槽各面的厚度忽略不计).已知a为5cm.
25. 做服装生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能售出A、B两种款式的服装合计30件,并且每售出一件A款式和B款式服装,甲店铺获利润分别为30元和35元,乙店铺获利润分别为26元和36元.某日,王老板进A款式服装36件,B款式服装24件,并将这批服装分配给两个店铺各30件.(1)、怎样将这60件服装分配给两个店铺,能使两个店铺在销售完这批服装后所获利润相同?(2)、怎样分配这60件服装能保证在甲店铺获利润不小于950元的前提下,王老板获利的总利润最大?最大的总利润是多少?26. 将一块a×b×c的长方体铁块(如图1所示,a<b<c,单位:cm)放入一长方体(如图2所示)水槽中,并以速度20cm3/s匀速向水槽注水,直至注满为止.若将铁块a×c面放至水槽的底面,则注水全过程中水槽的水深y (cm)与注水时间t (s)的函数图象如图3所示(水槽各面的厚度忽略不计).已知a为5cm. (1)、填空:水槽的深度为cm,b=cm;(2)、求水槽的底面积S和c的值;(3)、若将铁块的b×c面放至水槽的底面,求注水全过程中水槽的水深y(cm)与注水时间t(s)的函数关系,写出t的取值范围,并画出图象.27. 如图,已知点 ,经过A、B的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
(1)、填空:水槽的深度为cm,b=cm;(2)、求水槽的底面积S和c的值;(3)、若将铁块的b×c面放至水槽的底面,求注水全过程中水槽的水深y(cm)与注水时间t(s)的函数关系,写出t的取值范围,并画出图象.27. 如图,已知点 ,经过A、B的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒. (1)、用含t的代数式表示点P的坐标;(2)、过O作OC⊥AB于C,过C作CD⊥x轴于D,问:t为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时⊙P与直线CD的位置关系.28. 如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1 , 0),C(x2 , 0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.
(1)、用含t的代数式表示点P的坐标;(2)、过O作OC⊥AB于C,过C作CD⊥x轴于D,问:t为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时⊙P与直线CD的位置关系.28. 如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1 , 0),C(x2 , 0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q. (1)、求抛物线的解析式;(2)、当0<t≤8时,求△APC面积的最大值;(3)、当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、当0<t≤8时,求△APC面积的最大值;(3)、当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.