2016-2017学年甘肃省张掖四中九年级下学期期中数学试卷
试卷更新日期:2017-05-25 类型:期中考试
一、选择题
-
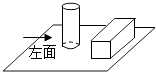
1. ﹣ 的相反数是( )A、3 B、﹣3 C、 D、﹣2. 今年“五•一”黄金周,我省实现社会消费的零售总额约为94亿元.若用科学记数法表示,则94亿可写为( )元A、0.94×109 B、9.4×109 C、9.4×107 D、9.4×1083. 桌面上按如图所示放着1个长方体和1个圆柱体,其左视图是( )
 A、
A、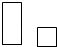 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、x2+x2=x4 B、(﹣a2)3=﹣a6 C、(a﹣b)2=a2﹣b2 D、3a2•2a3=6a65. 下列命题中,错误的是( )A、矩形的对角线互相平分且相等 B、等腰三角形底边上的中点到两腰的距离相等 C、等腰梯形的两条对角线相等 D、对角线互相垂直的四边形是菱形6. 不等式组 的整数解有( ) 个.A、1 B、2 C、3 D、47. 已知圆柱体体积V(m3)一定,则它的底面积Y(m2)与高x(m)之间的函数图象大致为( )A、
4. 下列运算正确的是( )A、x2+x2=x4 B、(﹣a2)3=﹣a6 C、(a﹣b)2=a2﹣b2 D、3a2•2a3=6a65. 下列命题中,错误的是( )A、矩形的对角线互相平分且相等 B、等腰三角形底边上的中点到两腰的距离相等 C、等腰梯形的两条对角线相等 D、对角线互相垂直的四边形是菱形6. 不等式组 的整数解有( ) 个.A、1 B、2 C、3 D、47. 已知圆柱体体积V(m3)一定,则它的底面积Y(m2)与高x(m)之间的函数图象大致为( )A、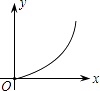 B、
B、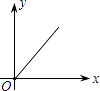 C、
C、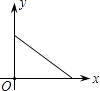 D、
D、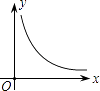 8. 若关于x的方程 有增根,求a的值( )A、0 B、﹣1 C、1 D、﹣29. 如图,正方形ABCD内接于⊙O,点E在劣弧AD上,则∠BEC等于( )
8. 若关于x的方程 有增根,求a的值( )A、0 B、﹣1 C、1 D、﹣29. 如图,正方形ABCD内接于⊙O,点E在劣弧AD上,则∠BEC等于( )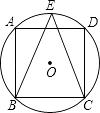 A、45° B、60° C、30° D、55°10. 二次函数y=ax2+bx+c的部分图象如图所示,则下列正确的说法有( )
A、45° B、60° C、30° D、55°10. 二次函数y=ax2+bx+c的部分图象如图所示,则下列正确的说法有( )①点P(ac,b)在第二象限;
②x>1时y随x的增大而增大;
③b2﹣4ac>0;
④关于x的一元二次方程ax2+bx+c=0解为x1=﹣1,x2=3;
⑤关于x的不等式ax2+bx+c>0 的解集为0<x<3.
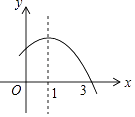 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. ﹣7的倒数是 .12. 分解因式:a3﹣9a= .
13. 函数y= 中自变量x的取值范围是 .14. 如图,a∥b,∠1=65°,∠2=140°,则∠3等于 .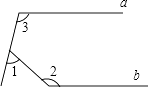 15. 在实数范围内定义运算“★”,其规则为a★b=a2﹣b2 , 则方程(4★3)★x=13的根为 .16. 将抛物线y=2x2先沿x轴方向向左平移2个单位,再沿y轴方向向下平移3个单位,所得抛物线的解析式是 .17. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′,若AB=4,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 . (结果保留π).
15. 在实数范围内定义运算“★”,其规则为a★b=a2﹣b2 , 则方程(4★3)★x=13的根为 .16. 将抛物线y=2x2先沿x轴方向向左平移2个单位,再沿y轴方向向下平移3个单位,所得抛物线的解析式是 .17. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′,若AB=4,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 . (结果保留π).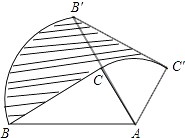 18. 如图,在你标有刻度的直线l上,从点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆…,按此规律,则第4个半圆的面积是第3个半圆面积的倍,第n个半圆的面积为 . (结果保留π)
18. 如图,在你标有刻度的直线l上,从点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆…,按此规律,则第4个半圆的面积是第3个半圆面积的倍,第n个半圆的面积为 . (结果保留π)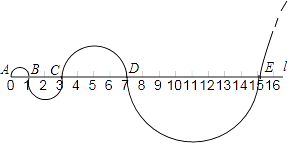
三、计算
-
19. 计算题(1)、计算:2 •sin45°﹣(﹣2012)0﹣|1﹣ |+(﹣ )﹣2(2)、先化简,再求值: ÷(1﹣ ),其中x=0.
四、解答题
-
20. 如图,⊙P的圆心为P(﹣3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.
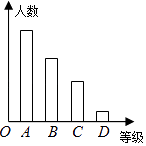
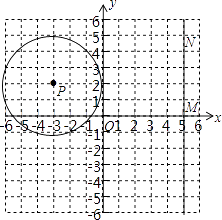 (1)、在图中作出⊙P关于y轴对称的⊙P′.根据作图直接写出⊙P′与直线MN的位置关系.(2)、若点N在(1)中的⊙P′上,求PN的长.21. 将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌面上,先从中随机的抽取一张卡片(不放回),将该卡片正面上的数字作为十位数字,再随机的抽取一张卡片,将该卡片正面上的数字作为个位数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.22. 某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:
(1)、在图中作出⊙P关于y轴对称的⊙P′.根据作图直接写出⊙P′与直线MN的位置关系.(2)、若点N在(1)中的⊙P′上,求PN的长.21. 将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌面上,先从中随机的抽取一张卡片(不放回),将该卡片正面上的数字作为十位数字,再随机的抽取一张卡片,将该卡片正面上的数字作为个位数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.22. 某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:①共抽测了人;②样本中B等级的频率是;
③如果要绘制扇形统计图,D等级在扇形统计图中所占的圆心角是度;
④该校九年级的毕业生共300人,假如“综合素质”等级为A或B的学生才能报考示范性高中,请你计算该校大约有名学生可以报考示范性高中.
 23. 某市在地铁施工期间,交管部门在施工路段设立了矩形路况警示牌BCEF(如图所示),已知立杆AB的高度是3米,从侧面D点测到路况警示牌顶端C点和底端B点的仰角分别是60°和45°,求路况警示牌宽BC的值.
23. 某市在地铁施工期间,交管部门在施工路段设立了矩形路况警示牌BCEF(如图所示),已知立杆AB的高度是3米,从侧面D点测到路况警示牌顶端C点和底端B点的仰角分别是60°和45°,求路况警示牌宽BC的值.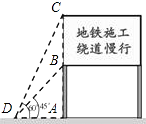 24. 某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).(1)、A、B两种花草每棵的价格分别是多少元?(2)、若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.25. 如图,在直角坐标系xOy中,直线y=mx与双曲线 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
24. 某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).(1)、A、B两种花草每棵的价格分别是多少元?(2)、若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.25. 如图,在直角坐标系xOy中,直线y=mx与双曲线 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.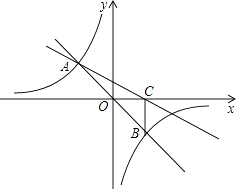 (1)、求m、n的值;(2)、求直线AC的解析式.26. 如图,在Rt△ABC中,∠C=90°,∠A=60°,点E,F分别在AB,AC上,把∠A沿着EF对折,使点A落在BC上点D处,且使ED⊥BC.
(1)、求m、n的值;(2)、求直线AC的解析式.26. 如图,在Rt△ABC中,∠C=90°,∠A=60°,点E,F分别在AB,AC上,把∠A沿着EF对折,使点A落在BC上点D处,且使ED⊥BC.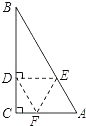 (1)、猜测AE与BE的数量关系,并说明理由;(2)、求证:四边形AEDF是菱形.27. 如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)、猜测AE与BE的数量关系,并说明理由;(2)、求证:四边形AEDF是菱形.27. 如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.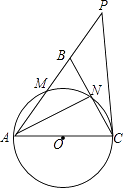 (1)、求证:直线CP是⊙O的切线;(2)、若BC=2 ,sin∠BCP= ,求点B到AC的距离.28. 已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)、求证:直线CP是⊙O的切线;(2)、若BC=2 ,sin∠BCP= ,求点B到AC的距离.28. 已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.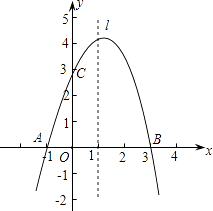 (1)、求抛物线的函数关系式;(2)、设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;(3)、在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.(4)、问:若抛物线顶点为D,点Q为直线AC上一动点,当△DOQ的周长最小时,求点Q的坐标
(1)、求抛物线的函数关系式;(2)、设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;(3)、在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.(4)、问:若抛物线顶点为D,点Q为直线AC上一动点,当△DOQ的周长最小时,求点Q的坐标
-